Контрольная работа №2
Введение в математический анализ.
Производная и ее приложения.
Вариант 6
Найти пределы функций, не пользуясь правилом Лопиталя.
а)
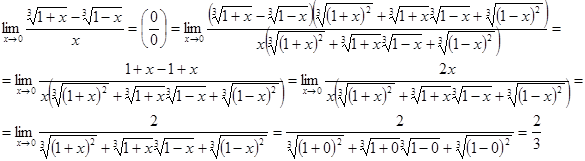
б)

в)

г)

6.3.16. Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать схематический чертеж.

Данная функция определена и непрерывна на интервалах (-∞;0], (0, 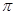 ],(
],(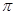 ;+∞), где она задана непрерывными элементарными функциями. Исследуем поведение функции. В точках перехода от одного аналитического выражения к другому, т.е. в точках при х=0 и х=
;+∞), где она задана непрерывными элементарными функциями. Исследуем поведение функции. В точках перехода от одного аналитического выражения к другому, т.е. в точках при х=0 и х= 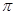 . Найдём односторонние пределы.
. Найдём односторонние пределы.
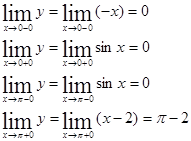
При х=0 функция имеет одинаковые односторонние пределы, значит, в этой точке функция непрерывна. Т.к. односторонние пределы при х= 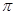 различны, то функция терпит в точке разрыв. А т.к. односторонние пределы конечны, то при х=
различны, то функция терпит в точке разрыв. А т.к. односторонние пределы конечны, то при х= 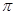 – точка разрыва первого рода. Функция имеет скачок в этой точке равный
– точка разрыва первого рода. Функция имеет скачок в этой точке равный 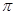 -2-0=
-2-0= 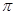 -2.
-2.
График этой функции:

7.1.6. Найдите производные 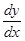 данных функций.
данных функций.
А) 

б) 

в) 

При каких линейных размерах закрытая цилиндрическая банка данной вместимости будет иметь наименьшую полную поверхность?
Решение.
Пусть R –радиус основания цилиндра, H- высота.

7.3.26. Методами дифференциального исчисления:
а) исследовать функцию и по результатам исследования построить ее график;
б) найти наименьшее и наибольшее значения заданной функции на отрезке [0,1].

1. Очевидно D (y) = (-¥;+¥).
2.  . Функция не является ни чётной, ни нечетной.
. Функция не является ни чётной, ни нечетной.
3. Найдем точки пересечения с осями координат:
с осью Оу: x = 0, то у=-е;
с осью Ох: y = 0, то х=1.
4. Определим критические точки. Для этого найдем производную y'.

Тогда y' = 0 имеет решение х =2/3 –абсцисса точки экстремума. Данная точка не входит в область. Определим знак первой производной на интервалах.

 y'(x)
y'(x)
– +
 2/3
2/3
Значит, на промежутке (2/3,+¥) функция возрастает, на промежутке (-¥,2/3)– убывает. Значит, при х=2/3 –минимум, у(2/3)=6,7.
5. Определим точки перегиба. Для этого найдем вторую производную y'' функции:

тогда y'' = 0 имеет решение при х=1/3. Это абсцисса точки перегиба.
Определим знак второй производной на области определения.
y''(x)


– +

1/3
Таким образом, при x Î(1/3, +¥) график функции вогнутый, x Î(-¥,1/3) график функции выпуклый.
6. Функция определена и непрерывна на всей области определения. Выясним, имеет ли график функции наклонную асимптоту у=кх+в.

Наклонных асимптот нет.
По результатам исследования строим график функции:
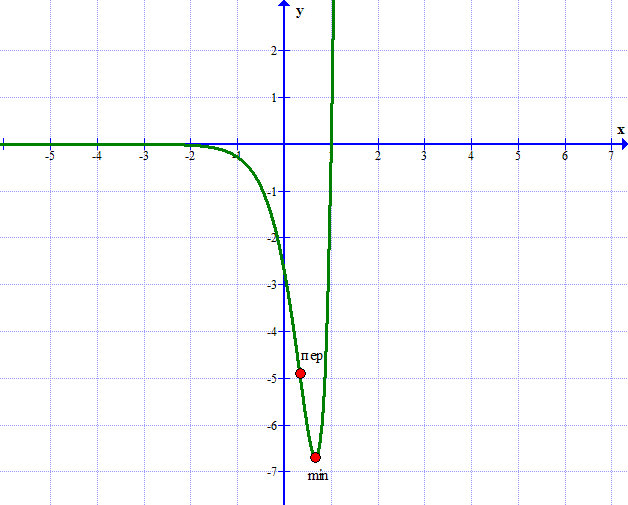
б) Функция непрерывна на отрезке [0;1]. Найдём производную 
В данном случае критической являются точка при х=2/3, причём точка принадлежит отрезку [0;1]. Вычислим значение на концах отрезка и в критической точке:

Таким образом, наименьшее значение данной функции равно -6,7 и получаем его при х=2/3 в критической точке, наибольшее равное 0 получаем при х=1 на правой границе.
Контрольная работа №3
Неопределенный и определенный интегралы. Функции нескольких переменных. Кратные интегралы.
Вариант 10
8.1.10. Найти неопределенные интегралы. Результаты проверить дифференцированием.
а)

Проверка:


б) 
Проверка:

в)
 ;
;
Проверим результат дифференцированием:

г)

Проверка:

Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
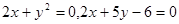
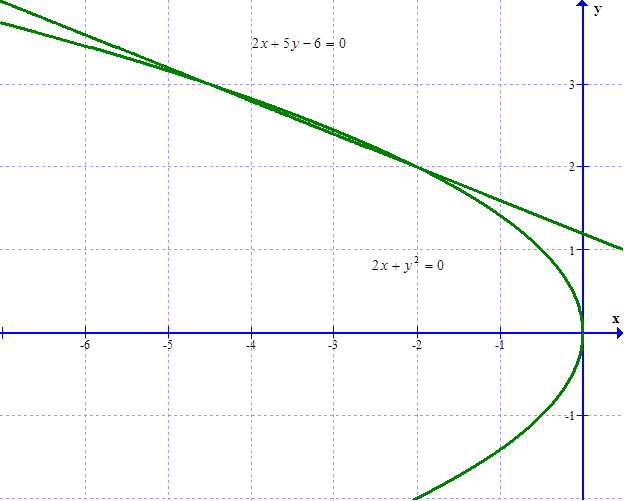
Найдем точки пересечения из решения системы уравнений:


9.1.16 Найти производные функции двух переменных  , если
, если  .
.
 и
и 
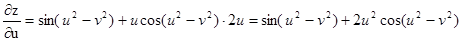 ,
,

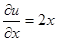 ,
,  ,
, 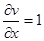 ,
, 
Тогда


9.1.56 Расставить пределы интегрирования в повторном интеграле для двойного интеграла  , и изменить порядок интегрирования.
, и изменить порядок интегрирования. 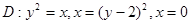 .
.

