Содержание
Введение …………………………………………………………………….…………………………….5
Часть 1 Теоретическая …………………………………………………………………………………6
1.1 История и понятие многогранников……………………….…………………………………….6
1.2 Связь геометрии и природы……………………………….……………………………………...8
1.3 Использование многогранников в мировой современной архитектуре……………………….9
1.4 Использование многогранников в архитектуре города Красноярска…………………………10
Часть 2 Практическая …………………………………………………………………………………..
2.1 Разработка внешнего вида здания, поиск оригинальной формы………………………………
2.2 Выбор и подготовка материалов для работы……………………………………………………
2.3 Изготовление макета………………………………………………………………………………..
2.4 Описание макета……………………………………………………………………………………
Часть 3 Заключение
Заключение, выводы, перспективы выполненной работы…………………………………………………
Список используемых источников………………………………………………………………………….
I. Введение
«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период.
Всё вокруг - геометрия.»
Ле Корбюзье
Актуальность:
На сегодняшний день стремительно идет развитие строительства городского мегаполиса, поэтому архитекторы стараются разнообразить внешний вид зданий и сооружений. Исследование многогранников может расширить область их применения в современной архитектуре.
Для меня, как для будущего абитуриента института Архитектуры и Дизайна, эта работа может быть перспективна в предстоящем обучении.
Тема моей работы это геометрическаяформа в архитектуре. Я хочу рассмотреть взаимосвязь математики, природы и искусства, и более конкретно исследовать использование многогранников в архитектуре.
|
|
Основная цель работы:
Используя правильные геометрические тела, создать макет современного здания.
Задачи:
v Изучить теоретический материал по теме использования многогранников в архитектуре.
v Рассмотреть применение многогранников в мировой архитектуре.
v Рассмотреть применение многогранников в красноярской архитектуре.
v Создать макет современного здания с использованием многогранников.
История и понятие многогранников
Геометрия – наука, изучающая формы, размеры и взаимное расположение геометрических фигур.
Разные формы материальных тел с древних времен наблюдал человек в природе: формы растений
и животных, гор и извилин рек, круга и серпа Луны и т. п. В процессе изучения человеком формы и практической деятельности накапливались геометрические сведения, вследствие чего, постепенно создавалась геометрическая наука.
Геометрические знания были изложены еще 2200 лет назад в “Началах” Евклида. В этой работе Евклид дал полное математическое описание правильных
многогранников. Он описывает структуру тетраэдра, октаэдра, куба, икосаэдра и
додекаэдра.
Многогранником называется тело, граница которого является объединением
конечного числа многоугольников.
Многогранником называется поверхность, составленная из многоугольников и
ограничивающая некоторое геометрическое тело.
С древнейших времен представления о красоте связаны с симметрией.
|
|
Наверное, этим объясняется интерес человека к многогранникам - удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей. Мы можем наблюдать, что многогранники окружают нас повсюду, как в природе, так и в искусстве человечества. Использовать многогранники в архитектуре люди стали еще до новой эры, так как форма куба и параллелепипеда является наиболее органичной и удобряй для строительства сооружений
Первые упоминания о многогранниках известны еще за три тысячи лет до
нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские
пирамиды и самую известную из них – пирамиду Хеопса. Это правильная
пирамида, в основании которой квадрат со стороной 233 м и высота которой
достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат
по геометрии. Правильные многогранники известны с древнейших времён. Их орнаментные
модели можно найти на резных каменных шарах, созданных в период позднего
неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях,
которыми люди играли на заре цивилизации, уже угадываются формы
правильных многогранников.
Начиная с 7 века до нашей эры в Древней Греции, создаются философские
школы. Большое значение в этих школах приобретают рассуждения, с помощью
которых удалось получать новые геометрические свойства.
Одной из первых и самых известных школ была Пифагорейская, названная в
честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики - это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов. Пифагорейцев поражала красота, совершенство, гармония этих фигур. Они считали правильные многогранники божественными фигурами и использовали в своих философских сочинениях:
|
|
первоосновам бытия - огню, воде земле, воздуху, придавалась форма
соответственно тетраэдра, икосаэдра, куба, октаэдра, а вся Вселенная имела
форму додекаэдра. Позже учение пифагорейцев о правильных многогранниках
изложил в своих трудах другой древнегреческий ученый, философ - идеалист
Платон. С тех пор правильные многогранники стали называться платоновыми
телами. (Рис. 1)
В наше время эту систему можно сравнить с четырьмя состояниями
вещества - твёрдым, жидким, газообразным и пламенным. Пятый многогранник
- додекаэдр символизировал весь мир и почитался главнейшим.
Это была одна из первых попыток ввести в науку идею систематизации.
Правильным многогранником называется многогранник, у которого все
грани правильные равные многоугольники, и все двугранные углы равны.
Но есть и такие многогранники, у которых все многогранные углы равны,
а грани - правильные, но разноименные правильные многоугольники.
Многогранники такого типа называются равноугольно-полуправильными
многогранниками. Впервые многогранники такое типа открыл Архимед. Им
подробно описаны 13 многогранников, которые позже в честь великого ученого
были названы телами Архимеда. Архимедовы тела частично получаются из
Платоновых тел в результате их усечения. Усеченное тело есть не что иное, как
тело с отрезанной верхушкой. Так могут быть получены первые пять
архимедовых тел: усеченный тетраэдр, усеченный октаэдр, усеченный икосаэдр,
усеченный куб, усеченный додекаэдр. Вторая группа архимедовых тел
представлена двумя многогранниками, являющимися результатом пересечения
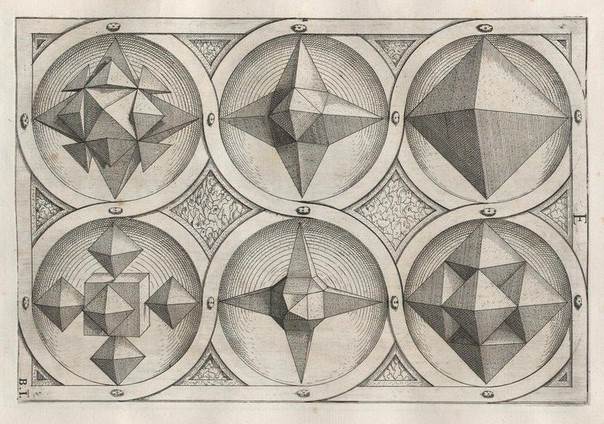двух платоновх тел подходящих размеров и расположенных так, что их центры
совпадают.
Рис. 1 Правильные и полуправильные платоновы тела.
1.2 Связь геометрии и природы
