При синтезе алгоритма оценки воспользуемся методом максимального правдоподобия (МП) [1-5]. Согласно этому методу необходимо формировать логарифм функционала отношения правдоподобия (ЛФОП)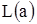 
как функцию неизвестной амплитуды. На основании результатов работ [1-3] выражение для ЛФОП можно представить в виде
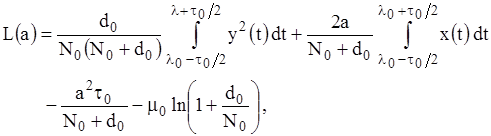(1.4)
где 
- отклик фильтра с импульсной характеристикой 
на реализацию наблюдаемых данных 
(1.1), причем передаточная функция 
этого фильтра удовлетворяет условию 
, 
, 
.
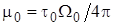Оценка максимального правдоподобия (ОМП) неизвестной амплитуды 
определяется как положение наибольшего максимума ЛФОП по переменной а:
. (1.5)
Положение наибольшего максимума ЛФОП 
является решением системы уравнения и неравенства:
, 
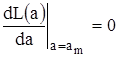. (1.6)
Согласно (1.3)
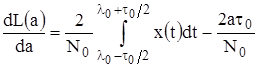. (1.7)
Тогда ОМП 
параметра 
запишется в виде
. 
(1.8)
Алгоритм (1.8) можно реализовать с помощью измерителя, структурная схема которого показана на рисунке.
Рисунок 1 - Максимально-правдоподобный измеритель математического ожидания случайного импульсного сигнала
Здесь обозначено: 1 - ключ открывающийся на время 
, 2 - интегратор, 3 - делитель.
Рассмотрим характеристики оценки (1.8). Поскольку аддитивная помеха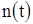 
является гауссовской, то ОМП (1.8) является гауссовской случайной величиной. Поэтому ее эффективность полностью (в статистическом смысле) характеризуется условными смещением 
, дисперсией 
и связанным с ними рассеянием 
.
Согласно определению условное смещение ОМП (1.8) найдем путем ее непосредственного усреднения по реализациям 
:
. (1.9)
Подставляя формулы (1.1), (1.2) в (1.9) и учитывая, что 
, получаем:
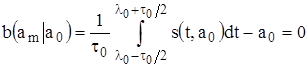. (1.10)
Таким образом, ОМП (1.8) при априори известных остальных параметрах импульса является условно (а, следовательно, и безусловно) несмещенной.
Аналогично можно найти условную дисперсию ОМП (1.9):
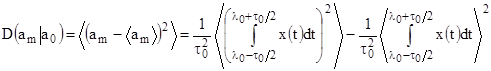(1.11)
Подставляя (1.1), (1.2) в (1.11), получаем:
(1.12)
Поскольку сигнал и шум статически независимы, то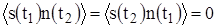 
. Кроме того, 
, 
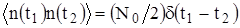, где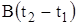 
- корреляционная функция процесса 
, а 
- дельта-функция. С учетом трех последних равенств из (1.12) получаем
.(1.13)
Для вычисления первого интеграла в (1.13) сделаем замену переменных: 
, 
. Тогда, полагая, что флуктуации процесса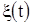 
являются «быстрыми», т.е. выполняется условие 
, имеем:
(1.14)
Для вычисления второго интеграла в (1.13) используем фильтрующее свойство δ-функции: 
. Тогда находим:
(1.15)
Подставляя (1.14), (1.15) в (1.13) для дисперсии оценки 
окончательно получаем
(1.16)
Поскольку ОМП (1.8) является несмещенной, то дисперсия оценки совпадает с ее рассеянием:
. (1.17)
Из формул (1.10), (1.16), (1.17) следует, что точность ОМП (1.8) МО случайного импульсного сигнала (1.2) не зависит от искаженного значения параметра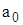 
. Дисперсия оценки МО, с одной стороны, возрастает с увеличением спектральной плотности 
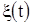и N0 процесса и шума 
, а, с другой стороны, уменьшается с увеличением длительности измеряемого импульса. Выражения (1.10), (1.16), (1.17) позволяют сделать обоснованный выбор длительности полезного сигнала в зависимости от требуемой эффективности МП измерителя и уровня аддитивных помех.