Теорема 5.5.(необходимое условие монотонности функции)
Если функция f (x) дифференцируема и не убывает на (а; b), то f ¢(x)³ 0 " х Î(а; b). Если функция f (x) дифференцируема и не возрастает на (а; b), то f ¢(x) £ 0 " х Î(а; b)
Доказательство: Пусть f (x) дифференцируема и не убывает на (а; b), т.е. " х 1, х 2 Î(а; b): х 1 < х 2 выполняется f (x 1) £ f (x 2). Возьмем любую точку х 0Î(а; b). В силу дифференцируемости функции f (x) существует
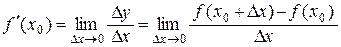 .
.
Если D х > 0, то х 0 +D х > х 0 и f (x 0 + D х) ³ f (x 0), откуда D у ³ 0, значит,  ³ 0.
³ 0.
Если D х < 0, то х 0 +D х < х 0 и f (x 0 + D х) £ f (x 0), откуда D у £0, но тогда  ³ 0. Таким образом,
³ 0. Таким образом, 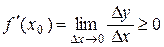 (согласно одной из теорем о предельном переходе в неравенстве).
(согласно одной из теорем о предельном переходе в неравенстве).
Аналогично доказывается второе утверждение теоремы. Проведите это доказательство самостоятельно.
Теорема 5.6.(достаточное условие монотонности)
Если f ¢(x) > 0 на (а, b), то f (x) строго возрастает на этом интервале. Если f ¢(x) < 0 на (а, b) то f (x) строго убывает на этом интервале.
Доказательство: 1) Пусть f ¢(x) > 0 на (а, b). Возьмем " х 1, х 2 Î(а; b): х 1 < х 2. По теореме Лагранжа имеем
 ),
),
где х 0 Î(х 1, х 2). Т.к. f ¢(x 0) > 0, а х 1 < х 2, т.е. х 2 – х 1 > 0, то f (x 2) – f (x 1) > 0, откуда f (x 2) > f (x 1) – функция возрастает. ЧТД
2) Случай убывания функции доказать самостоятельно.
Теоремы 5.5 и 5.6. нельзя объединить в одно необходимое и достаточное условие. Действительно, условие f ¢(x) > 0 на (а, b) не является необходимым условием возрастания функции f (x), т.к., например, для строго возрастающей функции f (x) = х 3 выполняется условие f ¢(x) = 3 х 2³ 0.
 С геометрической точки зрения теорема 5.6 утверждает, что если касательные к графику функции во всех точках интервала образуют острый угол с осью ОХ, то функции возрастающая. Убыванию функции соответствует тупой угол наклона касательной к оси ОХ (рис. 3).
С геометрической точки зрения теорема 5.6 утверждает, что если касательные к графику функции во всех точках интервала образуют острый угол с осью ОХ, то функции возрастающая. Убыванию функции соответствует тупой угол наклона касательной к оси ОХ (рис. 3).
Определение 5.1.
Точка х 0ÎD(f) называется точкой минимума функции f (x), если в некоторой окрестности этой точки выполняется неравенство f (x) ³ f (x 0). Значение f (x 0) называется минимумом функции.
Точка х 0ÎD(f) называется точкой максимума функции f (x), если в некоторой окрестности этой точки выполняется неравенство f (x) £ f (x 0). Значение f (x 0) называется максимумом функции.
Точки минимума и максимума называются точками экстремума функции. Значения функции в этих точках называются экстремумами функции.
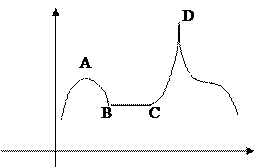 Если при х ¹ х 0 из окрестности точки х 0 выполняется строгое неравенство f (x) > f (x 0) или f (x) < f (x 0), то в этом случае говорят о строгом экстремуме в точке х 0, в противном случае – о нестрогом. На рисунке в точках А и D строгий максимум, в точках В и С нестрогий минимум.
Если при х ¹ х 0 из окрестности точки х 0 выполняется строгое неравенство f (x) > f (x 0) или f (x) < f (x 0), то в этом случае говорят о строгом экстремуме в точке х 0, в противном случае – о нестрогом. На рисунке в точках А и D строгий максимум, в точках В и С нестрогий минимум.
Может так случиться, что некоторый максимум функции f (x) окажется меньше ее минимума. Это не противоречит определению, т.к. в нем говорится об окрестности точки экстремума, т.е. о близлежащих к точке экстремума точках области определения функции. Поэтому для точек максимума и минимума используется термин «локальный» экстремум, т.е. связанный с определенным местом.
Теорема 5.7. (необходимое условие экстремума)
Если в точке х 0 функция имеет экстремум, то первая производная функции в этой точке либо равна нулю, либо не существует.
Доказательство: Пусть, для определенности, х 0 – точка максимума. Тогда для всех х из некоторой окрестности точки х 0 выполняется неравенство
D у = f (x) – f (x 0) < 0
Рассмотрим односторонние производные функции в точке х 0. В силу условия D у < 0  может быть либо конечным, отрицательным числом, либо равен -¥, либо равен 0. Аналогично,
может быть либо конечным, отрицательным числом, либо равен -¥, либо равен 0. Аналогично,  либо конечное положительное число, либо +¥, либо 0. Т.е.
либо конечное положительное число, либо +¥, либо 0. Т.е.
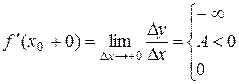 ,
, 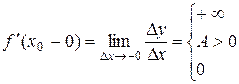
Отсюда следует, что f ¢(x 0) либо не существует (т.к. f ¢(x 0 +0) ¹ f ¢(x 0 – 0) или бесконечные), либо f ¢(x 0) = 0.
Геометрически теорема 5.7 утверждает, что в точке экстремума касательная к графику функции либо параллельна оси ОХ, либо параллельна ОУ, либо ее вообще нельзя провести (рис. 4).
 |
Таким образом, из теоремы следует, что точки экстремума следует искать среди точек, в которых производная функции либо равна нулю, либо не существует.
Точки, в которых производная функции равна нулю или не существует, называются критическими точками (первого рода). Точка экстремума обязательно является критической точкой, но не всякая критическая точка может быть точкой экстремума. Например, для функции у = х 3 точка х = 0 – критическая, т.к.
у ¢ (0) = 0,
но точкой экстремума она не является (вспомните график этой функции).
Теорема 5.8. (достаточное условие экстремума)
Пусть х 0 – критическая точка непрерывной и дифференцируемой в окрестности точки х0 функции f (x). Если при х<x 0 f ¢(x) > 0, а при x > х 0 f ¢(x)<0, то х 0 – точка максимума функции. Если при х < x 0 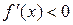 , а при x > х 0
, а при x > х 0 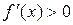 , то х 0 – точка минимума функции.
, то х 0 – точка минимума функции.
Доказательство:
Пусть при х<x 0 f ¢(x)>0, а при x > х 0 f ¢(x)<0. Рассмотрим интервал (а; b) – окрестность точки х 0. Поскольку при х Î(а; b), х<x 0 выполняется условие f ¢(x)>0, то на интервале (а; х 0), согласно теореме 5.6, функция возрастает, т.е. f (x)< f (x 0). А так как при x > х 0 f ¢(x)<0, то на интервале (х 0; b) функция убывает, значит, вновь выполняется неравенство f (x) < f (x 0). А это значит, что точка х 0 – точка максимума (причем, строгого). ЧТД.
Аналогично доказывается второе утверждение, касающееся точки минимума.
Найти интервалы возрастания, убывания и экстремумы функции y= f (x) можно, придерживаясь следующего алгоритма:
1) Найти область определения функции.
2) Найти производную f¢ (x) заданной функции.
3) Найти критические точки первого рода (точки возможного экстремума) из условия f¢ (x) = 0 или f¢ (x) не существует, х Î D (f).
4) Разбить область определения D (f) функции критическими точками на интервалы (внутри этих интервалов производная функции сохраняет знак).
5) Определить знак производной на каждом из полученных интервалов. На тех интервалах, где f¢ (x) > 0, функция возрастает, а там, где f¢ (x)< 0 – функция убывает.
6) Если при переходе через критическую точку слева направо:
· f¢ (x) меняет знак с «+ » на «–», то эта точка есть точка максимума функции;
· f¢ (x) меняет знак с «– » на «+ », то эта точка есть точка минимума функции;
· f¢ (x) не меняет знак, то в этой точке экстремума функции нет.