Математика за 27.04. Сдать до 29.04
Написать конспект, ознакомиться с примерами и выполнить
Практическую работу на платформе Фоксфорд «Физический смысл производной». Конспект прислать в вк. Практическую на платформе.
Тема: Физический смысл производной.
| Краткий справочный материал | Примеры решений задач | ||||||||||||||||||
Физический смысл производной.
Производной функции f в точке x0 называется число, к которому стремится разностное отношение
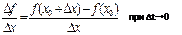 Мгновенной скоростью поступательного движения тела в момент времени t называется отношение очень малого перемещения ∆s к малому промежутку времени ∆t, за который произошло это перемещение
Мгновенной скоростью поступательного движения тела в момент времени t называется отношение очень малого перемещения ∆s к малому промежутку времени ∆t, за который произошло это перемещение
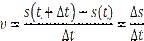 При ∆t→0, υ(t) =S’(t).
Скорость-производная от пути по времени.
Ускорениемназывается величина, равная отношению малого изменения скорости ∆υ к малому промежутку времени ∆t, за которое произошло это перемещение
При ∆t→0, υ(t) =S’(t).
Скорость-производная от пути по времени.
Ускорениемназывается величина, равная отношению малого изменения скорости ∆υ к малому промежутку времени ∆t, за которое произошло это перемещение
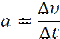 При Δt→0, а(t)=υ’(t).
Ускорение-производная от скорости по времени.
Отношение заряда Δ q, переносимого через поперечное сечение проводника за интервал времени Δ t, к этому интервалу времени называется силой тока.
При ∆t→0 i(t)=q’(t). Сила тока - производная от заряда по времени.
При ∆t→o, P=A’(t). Мощность – производная от работы по времени.
ЭДС индукции равна скорости изменения магнитного потока, ΔФ – изменение магнитного потока
При ∆t→0 ei = Ф’(t). ЭДС индукции– производная от магнитного потока по времени
Единицы измерения
Скорость – [м/с] Ускорение – [м/с2] Сила – [Н] Энергия – [Дж] При Δt→0, а(t)=υ’(t).
Ускорение-производная от скорости по времени.
Отношение заряда Δ q, переносимого через поперечное сечение проводника за интервал времени Δ t, к этому интервалу времени называется силой тока.
При ∆t→0 i(t)=q’(t). Сила тока - производная от заряда по времени.
При ∆t→o, P=A’(t). Мощность – производная от работы по времени.
ЭДС индукции равна скорости изменения магнитного потока, ΔФ – изменение магнитного потока
При ∆t→0 ei = Ф’(t). ЭДС индукции– производная от магнитного потока по времени
Единицы измерения
Скорость – [м/с] Ускорение – [м/с2] Сила – [Н] Энергия – [Дж]
| Пример 1. Материальная точка движется прямолинейно по закону x(t) = - t4+6t3 + 2t2+ 9t - 22, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3с.
Решение.
1. Найдем производную функции
x(t) = - t4 +6t3 + 2t2+ 9t - 22:
x'(t) = -4t3 + 18t2+ 4t + 9
2. Найдем значение производной в точке t = 3:
x'(3) = -4×33 + 18×32+ 4×3 + 9
x'(3) = 75.
Ответ: 75 м/с.
Пример 2. Материальная точка движется прямолинейно по закону x(t) = t3 - 6t2- 8t + 4, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 88 м/с?
Решение.
Найдем производную функции
x(t) = t3 - 6t2- 8t + 4:
x'(t) = 3t2- 12t - 8
По условию, скорость точки равна 88 м/с.
Получаем уравнение:
x'(t) = 3t2- 12t – 8 =88
Решим его:
3t2- 12t – 8 =88
3t2- 12t – 96 =0, разделим обе части уравнения на 3,
t2- 4t – 32 =0
t1 = 8, t2 = - 4 – не соответствует условию задачи: время не может быть отрицательным.
Ответ: 8
Пример 3. Точка движется по закону s(t)=2t³-3t (s – путь в метрах, t – время в секундах). Вычислите скорость движения точки, ее ускорение в момент времени 2с.
Пример 4 Маховик вращается вокруг оси по закону φ(t)= t4-5t. Найдите его угловую скорость ω в момент времени 2с (φ – угол вращения в радианах, ω – угловая скорость рад/с)
Пример 5 Тело массой 2 кг движется прямолинейно по закону х(t)=2-3t+2t².Найдите скорость тела и его кинетическую энергию через 3с после начала движения. Какая сила действует на тело в этот момент времени? (t измеряется в секундах, х – в метрах)
Пример 6 Точка совершает колебательные движения по закону х(t)=2sin3t. Докажите, что ускорение пропорционально координате х.
|
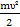 E=
E= 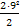 =82 Дж F=ma a(t)=υ’(t) a(t)=(-3+4t)’=4м/с F=2·4=8H Ответ: υ(3)= 9м/с; E=82 Дж; F=8H
=82 Дж F=ma a(t)=υ’(t) a(t)=(-3+4t)’=4м/с F=2·4=8H Ответ: υ(3)= 9м/с; E=82 Дж; F=8H