Динамическая система. Понятие о равновесном, периодическом и переходном процессах.

Динамическая система представляет собой математическую модель некоторого объекта, процесса или явления.

Динамическая система также может быть представлена как система, обладающая состоянием. При таком подходе, динамическая система описывает (в целом) динамику некоторого процесса, а именно: процесс перехода системы из одного состояния в другое. Фазовое пространство системы — совокупность всех допустимых состояний динамической системы. Таким образом, динамическая система характеризуется своим начальным состоянием и законом, по которому система переходит из начального состояние в другое.

Различают системы с дискретным временем и системы с непрерывным временем.

В системах с дискретным временем, которые традиционно называются каскадами, поведение системы (или, что то же самое, траектория системы в фазовом пространстве) описывается последовательностью состояний. В системах с непрерывным временем, которые традиционно называются потоками, состояние системы определено для каждого момента времени на вещественной или комплексной оси. Каскады и потоки являются основным предметом рассмотрения в символической и топологической динамике.

Динамическая система (как с дискретным, так и с непрерывным временем) часто описывается автономной системой дифференциальных уравнений, заданной в некоторой области и удовлетворяющей там условиям теоремы существования и единственности решения дифференциального уравнения. Положениям равновесия динамической системы соответствуют особые точки дифференциального уравнения, а замкнутые фазовые кривые — его периодическим решениям.

Основное содержание теории динамических систем — это исследование кривых, определяемых дифференциальными уравнениями. Сюда входит разбиение фазового пространства на траектории и исследование предельного поведения этих траекторий: поиск и классификация положений равновесия, выделение притягивающих (аттракторы) и отталкивающих (репеллеры) множеств (многообразий). Важнейшие понятие теории динамических систем — это устойчивость (способность системы сколь угодно долго оставаться около положения равновесия или на заданном многообразии) и грубость (сохранение свойств при малых изменениях структуры динамической системы; «грубая система — это такая, качественный характер движений которой не меняется при достаточно малом изменении параметров»^[1]).

Привлечение вероятностно-статистических представлений в эргодической теории динамических систем приводит к понятию динамической системы с инвариантной мерой.

Современная теория динамических систем является собирательным названием для исследований, где широко используются и эффективным образом сочетаются методы из различных разделов математики: топологии и алгебры, алгебраической геометрии и теории меры, теории дифференциальных форм, теории особенностей и катастроф.

Весьма тесно примыкает к таким современным разделам естествознания как неравновесная термодинамика, теория динамического хаоса,синергетика.

Определение

Пусть 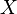— произвольное гладкое многообразие.

Динамической системой, заданной на гладком многообразии 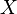, называется отображение 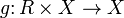, записываемое в параметрическом ви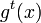де , где 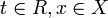, которое является дифференцируемым отображением, причём 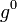— тождественное отображение пространства 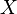. В случае стационарных обратимых систем однопараметрическое семейство 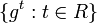образует группу преобразований топологического пространства 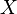, а значит, в частности, для любых 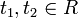выполняется тождество .

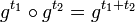Из дифференцируемости отображения 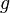следует, что функция 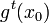является дифференцируемой функцией времени, её график расположен в расширенном фазовом пространстве 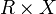и называется интегральной траекторией (кривой) динамической системы. Его проекция на пространство 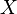, которое в носит название фазового пространства, называется фазовой траекторией (кривой) динамической системы.

Задание стационарной динамической системы эквивалентно разбиению фазового пространства на фазовые траектории. Задание динамической системы в общем случае эквивалентно разбиению расширенного фазового пространства на интегральные траектории.

Способы задания динамических систем

Для задания динамической системы необходимо описать её фазовое пространство 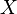, множество моментов времени 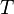и некоторое правило, описывающее движение точек фазового пространства со временем. Множество моментов времени 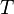может быть как интервалом вещественной прямой (тогда говорят, что время непрерывно), так и множеством целых или натуральных чисел (дискретное время). Во втором случае «движение» точки фазового пространства больше напоминает мгновенные «скачки» из одной точки в другую: траектория такой системы является не гладкой кривой, а просто множеством точек, и называется обычно орбитой. Тем не менее, несмотря на внешнее различие, между системами с непрерывным и дискретным временем имеется тесная связь: многие свойства являются общими для этих классов систем или легко переносятся с одного на другой.

Фазовые потоки

Пусть фазовое пространство 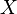представляет собой многомерное пространство или область в нем, а время непрерывно. Допустим, что нам известно, с какой скоростью движется каждая точка 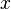фазового пространства. Иными словами, известна вектор-функция скорости 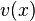. Тогда траектория точки 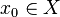будет решением автономного дифференциального уравнения 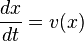с начальным условием 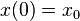. Заданная таким образом динамическая система называется фазовым потоком для автономного дифференциального уравнения.

Каскады

Пусть 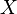— произвольное множество, и 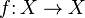— некоторое отображение множества 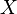на себя. Рассмотрим итерации этого отображения, то есть результаты его многократного применения к точкам фазового пространства. Они задают динамическую систему с фазовым пространством 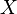и множеством моментов времени 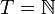. Действительно, будем считать, что произвольная точка 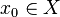за время 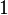переходит в точку 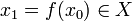. Тогда за время 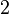эта точка перейдет в точку 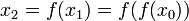и т. д.

Если отображение 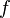обратимо, можно определить и обратные итерации: 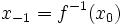, 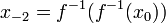и т. д. Тем самым получаем систему с множеством моментов времени .

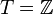Примеры

· Система дифференциальных уравнений

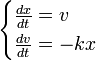
задает динамическую систему с непрерывным временем, называемую «гармоническим осциллятором». Её фазовым пространством является плоскость 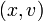, где 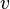— скорость точки 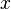. Гармонический осциллятор моделирует разнообразные колебательные процессы — например, поведение груза на пружине. Его фазовыми кривыми являются эллипсы с центром в нуле.

· Пусть 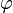— угол, задающий положение точки на единичной окружности. Отображение удвоения 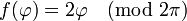, задаёт динамическую систему с дискретным временем, фазовым пространством которой является окружность.

· Быстро-медленные системы описывают процессы, одновременно развивающиеся в нескольких масштабах времени.

· Динамические системы, чьи уравнения могут быть получены посредством принципа наименьшего действия для удобно выбранной функции Лагранжа, известны как "лагранжевы динамические системы".

Режимы динамической системы

Следует различать три характерных режима, в которых может находиться динамическая система: равновесный, переходной и переодический.

Равновесный режим (равновесное состояние, состояние равновесия) – это такое состояние системы в котором она может находиться сколь угодно долго в отсутствие внешних возмущающих воздействий или при постоянных воздействиях. Однако надо понимать, что для экономических и организационных систем понятие «равновесие» применимо достаточно условно.

Пример. Простейший пример равновесия – шарик, лежащий на плоскости.

Под переходным режимом (процессом) будем понимать процесс движения динамической системы из некоторого начального состояния к какому-либо ее установившемуся режиму – равновесному или периодическому.

Периодическим режимом называется такой режим, когда система через равные промежутки приходит в одни и те же состояния.

2. Автоматическое регулирование в экономике. Условие Вальраса.

Леон Вальрас (1834—1910), математик по образованию, стал за­ниматься экономической теорией после того, как отец обратил его внимание на оригинальную работу французского математика О.Курно. Этот талантливый ученый был также и журналистом, и писате­лем, и директором банка. По происхождению он француз, но его часто называют швейцарским экономистом, поскольку много лет жизни (с 1870 г.) он отдал университету в Лозанне, возглавил ло­заннскую школу экономистов-математиков.

Известность пришла к Вальрасу после выхода в свет его книги "Элементы чистой политической экономии" (1874), в которой впер­вые была предложена модель общего экономического равновесия на базе теории спроса и предложения. Вальрас показывает взаимосвязь в экономической системе различных рынков. Рынок, с его точки зрения, — это некий аукционщик, объявляющий цены и оценива­ющий спрос и предложение до тех пор, пока не наступит равнове­сие. Вальрас считает, что свободная рыночная экономика и без ре­гулирования может достичь положения "общего равновесия", т.е. одновременного равновесия на всех рынках во всем хозяйстве. Теория общего рыночного равновесия отличается у Вальраса абсолютной изменчивостью всех экономических категорий и величин, т.е. она глубоко диалектична. Суть теории Вальраса отображена на схеме 5.

Схема 5. Равновесие Вальраса

В соответствии с этой теорией стоимость всегда относительна. По Вальрасу, она определяется сопоставлением интенсивности кон­кретной потребности в товаре с издержками его производства, при этом предполагается, что технологические возможности производ­ства заданы и известны. Такое сопоставление осуществляется не по отдельности для каждого товара, но в целом для всех товаров в данной хозяйственной системе, т.е. потребность в данном товаре и соответственно спрос на него зависят также от наличия других то­варов. Издержки производства данного товара, определяющие ус­ловия его предложения, зависят не только от технологии его соб­ственного производства, но и от всех альтернативных возможнос­тей использования потребляемых ресурсов. Следовательно, при дан­ном уровне развития производительных сил стоимость определяет­ся в точке равновесия между предельной общественной полезностью данного количества товара (с учетом воздействия на нее того или иного количества всех остальных товаров) и предельными обществен­ными издержками производства этого количества (с учетом альтер­нативных возможностей использования потребляемых ресурсов), т.е. выступает как равенство спроса и предложения не по одному дан­ному товару, а по всем товарам и услугам в экономике в целом.

Главным регулирующим механизмом в модели Вальраса являет­ся изменение структуры равновесных цен. Общий равновесный ана­лиз — это как бы "моментальный снимок" экономической систе­мы с заданными потребностями, ресурсами, технологией, т.е. данные параметры фиксированны и это помогает их математизации (сис­тема уравнений). Спрос на данный товар зависит не только от его цены, но и от цены на все остальные товары. Величина этого спро­са — функция всех существующих в экономике цен. Вальрас разра­ботал систему уравнений, представляющих собой условия равен­ства спроса и предложения на всех рынках в экономике с учетом бюджетного ограничения каждого потребителя и производителя. Доход каждого потребителя определяется количеством и ценой тех товаров и услуг (включая услуги труда или собственности), которые он продал на рынке. Поэтому потребитель не может купить товаров и услуг на сумму, большую, чем та, на которую он продал сам.

Общий рыночный спрос на каждые из товаров, услуг и факто­ров производства на рынке и их предложение — это совокупная сумма спроса в экономике. По стоимости она всегда будет равна совокупной сумме предложения. Это—закон Вальраса. И если у Сэя подобный закон предполагает, что предложение и спрос регулиру­ются автоматически, в разработанную им систему не были введе­ны деньги и ценные бумаги, то у Вальраса они включены в систе­му, а регулирующим механизмом выступает изменение равновес­ных цен.

Необходимо отметить огромный вклад Вальраса в разработку теории рынка. Недаром Й. Шумпетер назвал его книгу "священным писанием политэкономии". И действительно, Вальрас исследует си­стему не изолированного, а развитого товарного хозяйства, в кото­ром предложение и спрос определяются им как количество това­ров, соответственно предлагаемых и спрашиваемых при определен­ной цене. Влияние абсолютных потребностей на цену исключается. Вальрас рассуждает следующим образом.

Пусть Da, Db — спрос на товары а и b;

Sa, Sb — предложение товаров а и b;

Ра, Рb — цены товаров а и b;

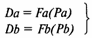— означает, что спрос на товар есть функция цены этого товара;

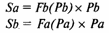— означает, что предложение есть произ­ведение спроса на другой товар на его цену.

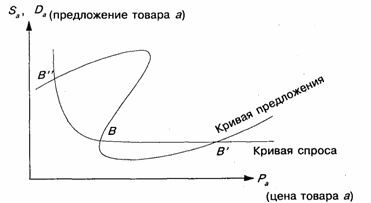
Рис. 3. Типы равновесии Вальраса

Спрос и предложение здесь соотносятся так же, как и в теории Сэя: поскольку деньги в систему явно не введены, одного товара предлагается столько, сколько будет спрашиваться другого, и на­оборот. Каждый товар выступает для другого эквивалентом его сто­имости: Pa = Va/Vb, Pb =Vb/Va, где Va, Vb — меновые ценности товаров а и b.

Предложение и спрос в модели Вальраса неравноправны: пред­ложение является зависимым от спроса, в то время как спрос зави­сит только от цены. В действительности предложение определяется не только влиянием спроса, но в значительной степени зависит от условий производства товаров.

Графически спрос и предложение можно представить так, как на рис. 3. Точки В" и В' описывают устойчивое равновесие (систе­ма при выходе из данных состояний возвращается в эти же состоя­ния), точка В — неустойчивое равновесие (при выходе из этого состояния система приходит в точки В' и В"). Равновесная цена показана на графике как точка пересечения кривых спроса и пред­ложения. Вальрас считает, что максимум эффективности по полез­ности для каждого участника обмена достигается тогда, когда от­ношение меновых ценностей товаров равно отношению их пре­дельных полезностей.

Модель Вальраса отражает идеальное состояние равенства спро­са и предложения при неразрывности актов купли-продажи, кото­рое в действительности, как правило, нарушается. Вальрас писал, что "максимум полезности для всех, с одной стороны, и единство цены — с другой, для продуктов ли на товарном рынке, или для услуг на рынке услуг, или для доходов на рынке капиталов — тако­вы два условия, согласно которым мир экономических интересов самостоятельно стремится к установлению, подобно тому как при­тяжение в прямом отношении к массе и в обратном к квадрату расстояния есть двоякое условие, по которому устанавливается по­рядок в мире астрономических движений".

Заслугой Вальраса является постановка проблемы общего равно­весия экономики как единой системы, в которой отдельные элемен­ты связаны через разделение труда и обмен. Модель общего эконо­мического равновесия Вальраса послужила основанием для разви­тия целого направления в экономической теории, в рамках кото­рого исследуются устойчивое глобальное динамическое равнове­сие, типы и факторы экономического роста. Влияние идей этого ученого хорошо заметно в работах А.Маршалла, других исследова­телей, разработавших неоклассические концепции экономическо­го роста.

Недостатком Вальрасовой модели является то, что в ней пока­зано готовое равновесие, но не описываются сами сделки, когда происходит нащупывание цен. Дж.Хикс отмечал, что Вальрас "мог сформулировать условия, касающиеся цен, установленных с уче­том данных ресурсов и данных предпочтений, но он не объяснил, что случится, если вкусы и ресурсы изменятся". Сегодня ученые применительно к современным условиям исследуют такие вопро­сы: во-первых, может ли одной структуре потребления соответ­ствовать не одна, а несколько систем меновых стоимостей; во-вто­рых, насколько устойчива равновесная система относительных цен, т.е. если какой-то внешний фактор нарушил равновесие, то вернется ли рынок к исходному равновесию после того, как воздей­ствие прекратилось.

Ответы на эти вопросы были даны во второй половине 70-х — 80-х годах нашего столетия. Это стало возможным благодаря при­влечению дифференциальной топологии и ее подраздела, известно­го как теория катастроф. Были получены следующие выводы. Для подавляющего большинства случаев изменение равновесной сис­темы относительных цен осуществляется плавно, эта система ус­тойчива, и близко от нее нет другой равновесной системы. В то же время нельзя исключить малое количество критических моментов, когда небольшое изменение количества товара может привести к резкому скачку стоимости и тогда равновесие неустойчиво. Иными словами, одним и тем же исходным условиям экономической сис­темы может соответствовать несколько систем равновесных цен.

Исключительно большое значение придавали модели Вальраса его ученик В.Парето, а также П. Самуэльсон, Й. Шумпетер, В. Леонтьев и др. "Вальрас первый нашел одну из этих систем уравне­ний, а именно ту, которая относится к свободной конкуренции; это капитальное открытие, — пишет В.Парето. — Конечно, наука уже развилась и будет беспрерывно развиваться в будущем, но это нисколько не умалит важности открытия Вальраса, точно так же как прогресс небесной механики нисколько не умалит значения "принципов Ньютона".