ДВУХМЕРНЫЕ И ТРЕХМЕРНЫЕ СИСТЕМЫ
Двухмерные и трехмерные системы совершают поступательное и вращательное движения. Например, электрон в атоме, связанный кулоновской силой с положительным зарядом ядра, вращается вокруг общего центра масс. Свободный электрон также может иметь неравный нулю угловой момент, когда его волновая поверхность вращается вокруг вектора скорости, образуя вихрь. В этом случае максимум вероятности обнаружения электрона перемещается по винтовой линии, на ее оси вероятность обнаружения электрона равна нулю благодаря центробежной силе. При отсутствии осевой скорости вероятность распределена по кольцу равномерно, и центр масс неподвижен. Такое вращение классической частицы без центростремительной силы запрещено теоремой о центре масс изолированной системы, согласно которой центр масс изолированной системы, на которую не действуют внешние силы, может двигаться лишь равномерно и прямолинейно, или покоиться.
В классической механике динамика вращательного движения описывается вектором момента импульса
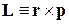 .
.
В декартовых координатах вектор  имеет проекции и квадрат модуля
имеет проекции и квадрат модуля
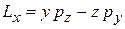 ,
,
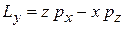 ,
,
 ,
,
 . (4.1)
. (4.1)
Формулы переходят друг в друга при циклической перестановке координат
 .
.
Операторы момента импульса
В квантовой механике вращение описывается операторами момента импульса, их собственными функциями и собственными значениями. Основные соотношения рассматривались в курсе «Методы математической физики», поэтому далее дается лишь обзор основных результатов.
Декартовые координаты. По правилу соответствия между классическими и квантовыми соотношениями величины в (4.1) заменяются операторами, тогда оператор момента импульса
 , (4.2)
, (4.2)
где с учетом
 ,
,  ,
, 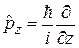 ,
,
операторы декартовых проекций момента импульса
 ,
,
 ;
;
 , (4.3)
, (4.3)
Оператор квадрата момента импульса
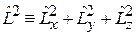 . (4.4)
. (4.4)
Операторы эрмитовые
 ,
, 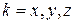 . (4.5)
. (4.5)
Доказательство (4.5) выносится на практическое занятие.
Перестановочные соотношения следуют из (4.3) с учетом
 ,
,  ,
,  ,
,
И имеют вид
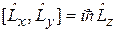 ,
,
 ,
,
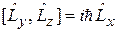 ,
,
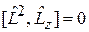 . (4.6)
. (4.6)
Из 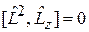 следует, что квадрат модуля
следует, что квадрат модуля 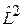 и проекция на декартовую ось
и проекция на декартовую ось  измеримы одновременно с неограниченной точностью, наборы их собственных функций совпадают. Собственные значения этих операторов – орбитальное число l и магнитное число m описывают вращательное состояние частицы.
измеримы одновременно с неограниченной точностью, наборы их собственных функций совпадают. Собственные значения этих операторов – орбитальное число l и магнитное число m описывают вращательное состояние частицы.
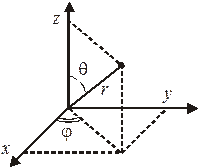
Сферические координаты  связаны с декартовыми координатами
связаны с декартовыми координатами  .
.
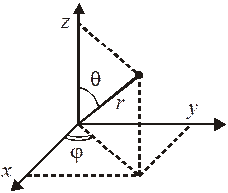
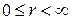 ;
; 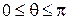 ;
; 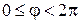 ,
,
 ,
,
 ,
,
 ,
,
Операторы в сферических координатах имеют вид
 , (4.7)
, (4.7)
 . (4.8)
. (4.8)
Оператор Лапласа в сферических координатах распадается на радиальную и угловую части
 . (4.9)
. (4.9)
Угловая часть содержит квадрат момента импульса 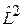 . Радиальная часть оператора Лапласа
. Радиальная часть оператора Лапласа
 (4.10)
(4.10)
выражается через радиальный импульс
 . (4.11)
. (4.11)
Выполняется
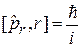 ,
,  . (4.12)
. (4.12)
Доказательство соотношений (4.10) – (4.12) выносится на практические занятия.
Повышающий и понижающий операторы
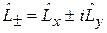 (4.13)
(4.13)
ступенчато изменяют собственные функции и собственные значения оператора  и удовлетворяют соотношениям
и удовлетворяют соотношениям
 ,
,
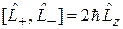 , (4.14)
, (4.14)
 , (4.15)
, (4.15)
 . (4.16)
. (4.16)
Оператор поворота 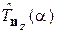 поворачивает углового состояния частицы
поворачивает углового состояния частицы  вокруг оси z на угол a
вокруг оси z на угол a
 . (4.17)
. (4.17)
Получим выражение оператора, разлагая  в ряд Тейлора и учитывая (4.7)
в ряд Тейлора и учитывая (4.7) 
 =
=  .
.
Сравниваем с (4.17), находим
 . (4.18)
. (4.18)
где  .
.
Обобщаем (4.18) на случай поворота вокруг единичного вектора n на угол a, отсчитываемый по правилу правого винта, получаем
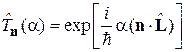 , (4.19)
, (4.19)
где оператор момента импульса является генератором поворота состояния частицы.
Сферическая функция
Сферическая функция  является собственнойфункцией взаимно коммутирующих операторов
является собственнойфункцией взаимно коммутирующих операторов 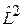 и
и 
 , (4.20)
, (4.20)
 , (4.21)
, (4.21)
где  – магнитное квантовое число, определяет проекцию орбитального момента L на ось z
– магнитное квантовое число, определяет проекцию орбитального момента L на ось z
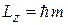 .
.
Орбитальное квантовое число  определяет модуль орбитального момента L
определяет модуль орбитального момента L
 . (4.22)
. (4.22)
Состояния 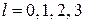 обозначаются в спектроскопии буквами s, p, d, f от англ. sharp – резкий, principal – главный, diffuse – расплывчатый, fundamental – фундаментальный.
обозначаются в спектроскопии буквами s, p, d, f от англ. sharp – резкий, principal – главный, diffuse – расплывчатый, fundamental – фундаментальный.
Количество проекций L на ось z равно числу возможных значений  , в результате число проекций
, в результате число проекций
 .
.
Направление L определяется углом θ с осью z. Угол квантуется
 . (4.23)
. (4.23)

Пространственное квантование при l = 3
Вектор L не может быть направлен вдоль оси z, поскольку максимальная проекция вектора не может превышать его модуль
 ,
,
тогда из (4.23) находим
 ,
,  .
.
Физическая причина в том, что определенность  приводит к неопределенностям некоммутирующих с ним
приводит к неопределенностям некоммутирующих с ним  и
и 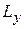 , которые дают вклад в
, которые дают вклад в 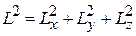 , поэтому
, поэтому  .
.
Из (4.15)

и (4.21)

получаем
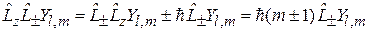 .
.
Следовательно, операторы  переводят состояние с собственным значением m в состояния с собственными значениями
переводят состояние с собственным значением m в состояния с собственными значениями  , то есть
, то есть  повышает у состояния число m на единицу, а
повышает у состояния число m на единицу, а  понижает на единицу.
понижает на единицу.
Выполняется
 , (4.24)
, (4.24)
полученное в курсе «Методы математической физики».
Выражение для сферической функции  . В сферических координатах изменения углов θ и φ происходят независимо, поэтому функция состояния факторизуется
. В сферических координатах изменения углов θ и φ происходят независимо, поэтому функция состояния факторизуется
 .
.
В уравнение на собственную функцию (4.21)

подставляем оператор (4.7)
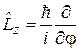
получаем уравнение
 . (4.25)
. (4.25)
Накладываем условие периодичности
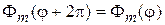 . (4.26)
. (4.26)
Из (4.25) и (4.26) получаем
 ,
,  (4.27)
(4.27)
Условие периодичности (4.26) привело к квантованию числа m. На основании

функции  , где
, где  , удовлетворяют условию ортонормированности
, удовлетворяют условию ортонормированности
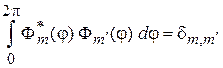 . (4.28)
. (4.28)
Для оператора квадрата момента импульса (4.8)

уравнение на собственную функцию (4.20)

дает дифференциальное уравнение
 .
.
Решение в виде

с учетом (4.27)

приводит к уравнению для 
 . (4.29)
. (4.29)
Уравнение совпадает с уравнением для присоединенных функций Лежандра  , тогда
, тогда  ,
,
 .
.
Постоянный множитель  определяется из условия нормировки
определяется из условия нормировки
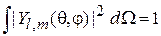 ,
,  .
.
В результате
 . (4.30)
. (4.30)
Выполняются
 , (4.31)
, (4.31)
 ,
,  ,
,
 , (4.32)
, (4.32)
и условие ортонормированности
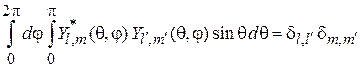 . (4.33)
. (4.33)
Инверсия координат  соответствует замене
соответствует замене
 ,
,  ,
,
тогда
 . (4.34)
. (4.34)
Четность состояния, описываемого сферической функцией, совпадает с четностью орбитального числа l.