Лекция №6
Содержание:
1. Разложение сигналов в обобщенный ряд Фурье.
2. Разложение аналогового сигнала в базисе Уолша.
3. Тригонометрическая и комплексная форма ряда Фурье.
4. Спектральное и временное представление сигналов.
Пусть s (t) - одиночный импульсный сигнал конечной длительности. Дополнив его мысленно такими же сигналами, периодически следующими через некоторый интервал времени T, получим изученную ранее периодическую последовательность Sпер (t), которая может быть представлена в виде комплексного ряда Фурье
(4.1) с коэффициентами 
(4.2)
Для того чтобы вернуться к одиночному импульсному сигналу, устремим к бесконечности период повторения Т. При этом, очевидно:
1. Частоты соседних гармоник nω1 и (n + l)ω1 окажутся сколь угодно близкими, так что в формулах (4.1) и (4.2) дискретную переменную nω1 можно заменить непрерывной переменной ω — текущей частотой.
2. Амплитудные коэффициенты Сn станут неограниченными малыми из-за наличия величины Т в знаменателе формулы (4.2).
Наша задача состоит теперь в нахождении предельного вида формулы (4.1) при T→∞.
Воспользуемся тем, что коэффициенты ряда Фурье образуют комплексно-сопряженные пары. Каждой такой паре отвечает гармоническое колебание с комплексной амплитудой 
.
Рассмотрим малый интервал частот Δω, образующий окрестность некоторого выбранного значения частоты ω0. В пределах этого интервала будет содержаться N=Δω/ω1= ΔωT/(2π) отдельных пар спектральных составляющих, частоты которых отличаются сколь угодно мало. Поэтому составляющие можно складывать так, как будто все они имеют одну и ту же частоту и характеризуются одинаковыми комплексными амплитудами 
В результате находим комплексную амплитуду эквивалентного гармонического сигнала, отображающего вклад всех спектральных составляющих, содержащихся внутри интервала Δω:
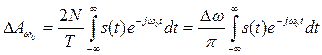. (4.3)
Функция 
(4.4)
носит название спектральной плотности сигнала s (t). Формула (4.4) осуществляет преобразование Фурье данного сигнала.
Решим обратную задачу спектральной теории сигналов: найдем сигнал по его спектральной плотности, которую будем считать заданной.
Положим вновь, что непериодический сигнал получается из периодической последовательности, когда ее период устремляется к бесконечности. Воспользовавшись формулами (4.1) и (4.2), запишем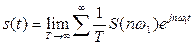 
Входящий сюда коэффициент 1/T пропорционален разности между частотами соседних гармоник: 
при любом целом п. Таким образом, 
Поскольку в пределе частотные интервалы между соседними гармониками неограниченно сокращаются, последнюю сумму следует заменить интегралом
. (4.5)
Эта важная формула называется обратным преобразованием Фурье для сигнала s(t).
Сформулируем окончательно фундаментальный результат: сигнал s(t) и его спектральная плотность S(ω) взаимно однозначно связаны прямым и обратным преобразованиями Фурье:
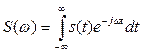, (4.6)
Спектральное представление сигналов открывает прямой путь к анализу прохождения сигналов через широкий класс радиотехнических цепей, устройств и систем.
Сигналу s(t) можно сопоставить его спектральную плотность s(ω) в том случае, если этот сигнал абсолютно интегрируем, т. е. существует интеграл
.
Подобное условие значительно сужает класс допустимых сигналов. Так, в указанном классическом смысле невозможно говорить о спектральной плотности гармонического сигнала и (t) =Umcosω0t, существующего на всей бесконечной оси времени.
Важный вывод: чем меньше длительность импульса, тем шире его спектр.
Под шириной спектра понимают частотный интервал, в пределах которого модуль спектральной плотности не меньше некоторого наперед заданного уровня, например изменяется в пределах от |S|max, до 0.1|S|max.
Произведение ширины спектра импульса на его длительность есть постоянное число, зависящее только от формы импульса и, как правило, имеющее порядок единицы:
Чем короче длительность импульса, тем шире должна быть полоса пропускания соответствующего усилителя. Короткие импульсные помехи имеют широкий спектр и поэтому могут ухудшать условия радиоприема в значительной полосе частот.
Математические модели многих сигналов, широко применяемых в радиотехнике, не удовлетворяют условию абсолютной интегрируемости, поэтому метод преобразований Фурье в обычном виде к ним неприменим. Однако можно говорить о спектральных плотностях таких сигналов, если допустить, что эти плотности описываются обобщенными функциями.
Пусть два сигнала и(t) и v(t), в общем случае комплексно-значные, определены своими обратными преобразованиямиФурье.
Найдем скалярное произведение этих сигналов, выразив один из них, например v(t), через его спектральную плотность:
Полученное соотношение представляет собой обобщенную формулу Рэлея. Легко запоминающаяся трактовка этой формулы такова: скалярное произведение двух сигналов с точностью до коэффициента пропорционально скалярному произведению их спектральных плотностей. Если сигналы тождественно совпадают, то скалярное произведение становится равным энергии
. (4.7)
Назовем взаимным энергетическим спектром вещественных сигналов u (t) и v (t) функцию
, (4.8)
такую, что
, (4.9)
Нетрудно заметить, что Re W uv (ω)—четная, а Im W uv (ω)—нечетная функция частоты. Вклад в интеграл (4.9) дает только вещественная часть, поэтому
(4.10)
Последняя формула дает возможность проанализировать «тонкую структуру» взаимосвязи сигналов.
Более того, обобщенная формула Рэлея, представленная в виде (4.10), указывает на принципиальный путь, позволяющий уменьшить степень связи между двумя сигналами, добившись в пределе их ортогональности. Для этого один из сигналов необходимо подвергнуть обработке в особой физической системе, называемой частотным фильтром. К этому фильтру предъявляется требование: не пропускать на выход спектральные составляющие, находящиеся в пределах частотного интервала, где вещественная часть взаимного энергетического спектра велика. Частотная зависимость коэффициента передачи такого ортогонализирующего фильтра будет обладать резко выраженным минимумом в пределах указанной области частот.
Спектральное представление энергии сигнала легко получить из обобщенной формулы Рэлея, если в ней сигналы и(t) и v(t) считать одинаковыми. Формула (4.8), выражающая спектральную плотность энергии, приобретает вид
. (4.11)
Величина Wu(ω) носит название спектральной плотности энергии сигнала и(t), или, короче, его энергетического спектра. Формула (3.2) при этом запишется так:
. (4.12)
Соотношение (4.12) известно как формула Рэлея (в узком смысле), которая констатирует следующее: энергия любого сигнала есть результат суммирования вкладов от различных интервалов частотной оси.
Изучая сигнал с помощью его энергетического спектра, мы неизбежно теряем информацию, которая заключена в фазовом спектре сигнала, поскольку в соответствии с формулой (4.11) энергетический спектр есть квадрат модуля спектральной плотности и не зависит от ее фазы. В современных радиоэлектронных комплексах выбор сигналов диктуется, прежде всего, не техническими удобствами их генерирования, преобразования и приема, а возможностью оптимального решения задач, предусмотренных при проектировании системы.
Обратимся к упрощенной идее работы импульсного радиолокатора, предназначенного для измерения дальности до цели. Здесь информация об объекте измерения заложена в величине τ — задержке по времени между зондирующим и принятым сигналами. Формы зондирующего и (t) и принятого и (t-τ) сигналов одинаковы при любых задержках.
Структурная схема устройства обработки радиолокационных сигналов, предназначенного для измерения дальности может выглядеть так, как это изображено на рис. 4.1.
Система состоит из набора элементов, осуществляющих задержку «эталонного» передаваемого сигнала на некоторые фиксированные отрезки времени τ1, τ2, …, τ N. Задержанные сигналы вместе с принятым сигналом подаются на устройства сравнения, действующие в соответствии с принципом: сигнал на выходе появляется лишь при условии, что оба входных колебания являются «копиями» друг друга. Зная номер канала, в котором происходит указанное событие, можно измерить задержку, а значит, и дальность до цели.
Рис. 4.1. Устройство для измерения времени задержки сигналов
Подобное устройство будет работать тем точнее, чем в большей степени разнятся друг от друга сигнал и его «копия», смещенная во времени.