Определение частот вращения и угловых скоростей на валах привода

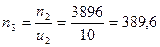об/мин;

1/с;

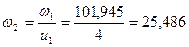1/c;

Определение крутящих моментов на валах привода

Т_дв=N_тр/ώ_дв=12058/101,945=118,283 Н·м

Т₁=Т_дв·η_м·η_под=118,283·0,98·0,99=115,92 Н·м

Т₂=Т₁·и₁·η_зп·η_под=115,92·4·0,97·0,99=445,262 Н·м

Т₃=Т₂·η_м=445,262·0,98=436,356 Н·м

Т₄=Т₃·и₂·η_цп=436,356·10·0,96=4319,932 Н·м

3.3 Расчёт зубчатой передачи редуктора

Принимаем для шестерни z₁ сталь 40Х, термическая обработка- улучшение, твёрдость НВ 245; для колеса z₂ – сталь 40Х, термическая обработка – улучшение, твёрдость НВ 245, [3, стр.34].

Допускаемые контактные напряжения, [3, стр.33]:

где - предел контактной выносливости при базовом числе циклов, МПа; - коэффициент долговечности; - коэффициент безопасности.

Рассчитаем , [3, стр.34]:

для шестерни ;

для колеса .

Рассчитаем коэффициент долговечности , [3, стр.33].

где N_HO –число циклов напряжений, N_HO =10⁷, [3, стр.34];

N_H_Е - эквивалентное число циклов перемены напряжений.

Эквивалентное число циклов перемены напряжений при постоянной нагрузке:

N_H_Е= 60n₃ ּ с ּ t_∑,

где n₃- частота вращения ведомого колеса z₂; с-количество контактов зуба за один оборот колеса; t_∑ - суммарное время работы передачи при постоянном режиме, час;

По условию срок службы привода (h = 12000 ч.) в часах переводим в срок службы привода в годах L_год = 1,36 лет.

Фактическая продолжительность работы в течение одного года (300 рабочих дней) при работе в две смены по 8 часов:

ч.

Тогда, N_H_Е= 60n₃ ּ с ּ t_∑= 60·120·1·6528 = 4,7·10⁷.

Тогда,

При N_H_Е≥ N_HO принимают =1, [3, стр.33].

Принимаем коэффициент = 1.1, [3, стр.33].

Расчётное допускаемое напряжение по шестерне:

Расчётное допускаемое напряжение по колесу:

Для прямозубых колес расчетное допускаемое контактное напряжение определяют по формуле, [3, стр.35]:

Требуемое условие выполнено.

Межосевое расстояние из условия контактной выносливости активных поверхностей зубьев, [3, стр.32]:

где К_a – вспомогательный коэффициент, для прямозубых передач К_a = 49.5, [3, стр.32]; - коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца; принимаем =1.25;

- коэффициент ширины венца по межосевому расстоянию, принимаем = 0.25;

Т₃ – вращающий момент на колесе z₂.

Тогда,

Принимаем по ГОСТ 2185 - 66 = 200 мм.

Нормальный модуль зацепления, [3, стр.36]:

Принимаем по ГОСТ 9563- 60 = 4 мм.

Принимаем предварительно угол наклона зубьев и определим числа зубьев шестерни и колеса, [3, стр.37]:

Принимаем z₁ = 20; тогда .

Рассчитаем основные размеры шестерни и колеса, [3, стр.37].

Диаметры делительные:

;

Проверка:

Диаметры вершин зубьев:

;

Диаметры впадин зубьев:

;

Ширина колеса:

;

Принимаем

Определим коэффициент ширины шестерни по диаметру:

Окружная скорость колёс:

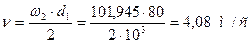При данной скорости назначаем 8-ю степень точности.

Коэффициент нагрузки для проверки контактных напряжений:

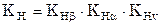где К_Нβ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца; К_Нα – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями; К_Нν – коэффициент, учитывающий влияние динамической нагрузки, возникающей в зацеплении.

Принимаем коэффициенты, [3, стр.39]: К_Нβ =1,024; К_Нα= 1,088; К_Нν = 1,0.

Тогда, К_Н =1,024·1,088·1,0 =1,114.

Проверяем контактные напряжения, [3, стр.31]:

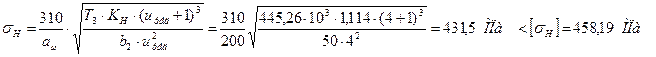
Силы, действующие в зацеплении, [3, стр.158]:

Окружная ;

Радиальная .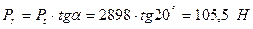

Проверим зубья на выносливость по напряжениям изгиба, [3, стр.46]:

где Р_t – окружная сила, Н; К_F – коэффициент нагрузки; Y_F – коэффициент прочности зуба; Y_β – коэффициент, учитывающий повышение прочности косых зубьев по сравнению с прямыми; К_Fα - коэффициент, учитывающий неравномерность распределения нагрузки между зубьями. Определяем коэффициент нагрузки, [3, стр.42]:

где - коэффициент, учитывающий неравномерность распределения нагрузки длине зубьев; - коэффициент, учитывающий динамическое действие нагрузки.

По рекомендациям [3, стр.43] принимаем =1,64; =1,45.

Тогда, К_F = 1,64 · 1,45 =2,378.

Y_F – коэффициент прочности зуба по местным напряжениям

для шестерни Y_F₁= 4,02;

для колеса Y_F₂ = 4,02.

Определяем допускаемое напряжение, [3, стр.43]:

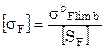где - предел выносливости при нулевом цикле изгиба, МПа;

- коэффициент запаса прочности.

По табл.3.9 [3, стр.44] принимаем для стали 40Х при твёрдости НВ ≤ 350 .

Для шестерни МПа;

для колеса МПа.

Коэффициент запаса прочности, [3, стр.44]:

где - коэффициент запаса прочности, учитывающий нестабильность свойств материала зубчатых колёс; - коэффициент запаса прочности, учитывающий способ получения заготовки зубчатого колёса.

Принимаем по рекомендациям [3, стр.44-45]: =1,75; =1,0;

тогда = 1,75 · 1,0 = 1,75 МПа.

Допускаемые напряжения и отношения :

для шестерни

; ;

для колеса

; .

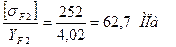Дальнейшую проверку проводим для зубьев шестерни.

- коэффициент, учитывающий повышение прочности косых зубьев по сравнению с прямыми, [3, стр.46]. Для прямозубых колёс

Проверяем зуб шестерни:

Условие прочности на изгиб выполнено.

3.4 Предварительный расчёт валов редуктора

Расчёт ведущего вала

Диаметр выходного конца ведущего вала определяют из условия прочности на кручение при допускаемых напряжениях на кручение = 25 МПа, [3, стр.161]. Невысокое значение напряжения принято с учётом того, что ведущий вал испытывает изгиб от натяжения клиноремённой передачи.

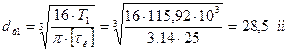
Полученный диаметр округляем до ближайшего большего значения из стандартного ряда, [2, стр.161]: d_в1 = 36 мм. Диаметр вала увеличен, т.к. вал двигателя соединен через муфту.

Диаметр вала под подшипниками d_п1 =40 мм;

диаметр вала под шестерней d_ш = d_п1 +r*2 мм

r=2 по табл.: d_ш = 40+3*2=46 мм; принимаем d_ш =46 мм;

Предварительно назначаем по ГОСТ 8338-75 подшипники шариковые радиальные однорядные лёгкой серии; обозначение 208.