Обработка ведется в специальной ведомости (Таблица 1.4) в следующей последовательности:
1. В графе 4 записывают исходный дирекционный угол начальной стороны αп / п85 – п / п84= 11°23’37” и исходный дирекционный угол конечной стороны αп / п83 – п / п82= 137°45'55". Исходные дирекционные углы выделены жирным шрифтом.
2. Вычисляется сумма измеренных углов в ходе (значения измеренных углов записаны в графе 2
∑ βпр= 202°48'00"+199°12'30"+70°10'00"+106°46'30"+194°39'00" = 773°36'00"
Если через αн и αк обозначим дирекционные углы в начале и конце теодолитного хода, которые заданы как неизменные и безошибочные, то в этом случае должно выполняться равенство:
α к =α н +180°⋅ n−  , (1.11)
, (1.11)
где n – число вершин, на которых измерялись углы.
Если это равенство переписать для ∑β, то полученное выражение можно использовать для вычисления теоретической суммы углов в ходе. Отсюда
∑ β теор=αн − αк + 180°⋅ n. (1.12)
∑ β теор=11°23'37"-137°45'55"+ 180°⋅ 5=773°37'42"
Вследствие ошибок измерений углов практическая сумма измеренных горизонтальных углов не равна теоретической сумме горизонтальных углов, разность между ними называют угловой невязкой.
∑ β теор≠ ∑ β пр
3. Вычисляется угловая невязка хода. Разница между ∑ β пр и ∑ β теор и составляет угловую невязку в разомкнутом теодолитном ходе.
fβ = ∑ βпр − ∑ βтеор (1.13)
f β = 773°36'00"− 773°37'42"= - 0°01'42"
Полученную невязку сравнивают с допустимой, которая вычисляется по формуле:
fβ доп = 1 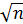 (1.14)
(1.14)
где n – число измеренных углов.
В нашем примере f β доп= 1 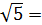 2,24 ′. Если выполняется неравенство f β ≤ f β доп, то f β делят на количество углов и получают величину поправки, которую вводят в каждый измеренный горизонтальный угол с обратным знаком:
2,24 ′. Если выполняется неравенство f β ≤ f β доп, то f β делят на количество углов и получают величину поправки, которую вводят в каждый измеренный горизонтальный угол с обратным знаком:
δβ = −  (1.15)
(1.15)
Поправки вычисляются до целых секунд. Должно выполняться равенство ∑δ β = − f β. К измеренным углам прибавляют поправку со своим знаком, результат записывают в графу 3.
β испр = βизм + δβ (1.16)
Контролем правильности исправления углов служит равенство
∑ β испр= ∑ β теор (1.17)
После уравнивания углов вычисляют дирекционные углы всех сторон хода по формуле:
α n + 1 =α n +180°−β испр. (1.18)
Дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180º и минус правый (исправленный) угол хода, образованный этими сторонами.
Пример.
αп/п84−1= αп/п85−п/п84+180° − βп/п 84 = 11°23'37"+180° −202°48′20" = 348°35'17"
Затем вычисляются значения румбов r по формулам зависимости между ними (таблица 1.2) и дирекционными углами, помня, что румб – это острый угол между стороной теодолитного хода и ближайшим к ней направлением меридиана – северным или южным. Румбы записываются в графы 8, 9 таблицы.
Таблица 1.2 - Переводдирекционныхугловврумбы.
| Номер четверти | Название четверти | Формула перевода |
| I | СВ | r I=α |
| II | ЮВ | r II=180º-α |
| III | ЮЗ | r III=α-180º |
| IV | СЗ | r IV=360º-α |
В графу 10 ведомости координат выписывают измеренные горизонтальные проложения из таблицы 1.1.
Таблица 1.3 - Знакиприращенийпрямоугольныхкоординат
| Приращения | Названия румбов | |||
| СВ | ЮВ | ЮЗ | СЗ | |
| ∆ x | + | - | - | + |
| ∆ y | + | + | - | - |
В соответствии с румбами записывают знаки приращений координат (таблица 1.3) и с помощью микрокалькулятора с функциями вычисляют приращения координат по формулам:
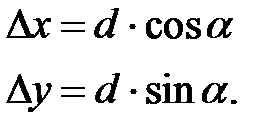 (1.19)
(1.19)
где d - горизонтальные проложения сторон теодолитного хода,
α – дирекционные углы сторон теодолитного хода,
Приращения координат записываются в графы 11 и 12 соответственно для Х и Y.
Например
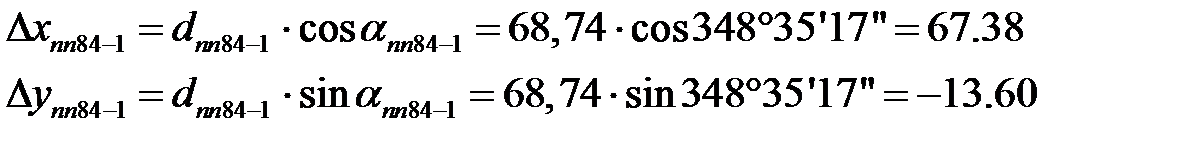
Для контроля правильности измерения длин сторон теодолитного хода и оценки точности вычисляют невязки f x и f y приращений координат по координатным осям X и Y путем суммирования приращений координат:
 =67,38+163,81+19,52-97,55=153,16 м
=67,38+163,81+19,52-97,55=153,16 м
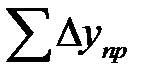 =-13,60-96,97+102,34+50,95=42,72 м
=-13,60-96,97+102,34+50,95=42,72 м
S  xтеор. = xПП83–xПП84=364,75-211,65=153,10м
xтеор. = xПП83–xПП84=364,75-211,65=153,10м
S  yтеор=yПП83–yПП84=510,60-467,75 = 42,85 м
yтеор=yПП83–yПП84=510,60-467,75 = 42,85 м
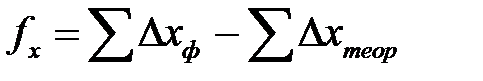 =153,16-153,10=0,06 м
=153,16-153,10=0,06 м
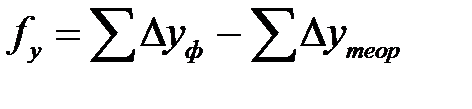 =42,72-42,85=-0,13
=42,72-42,85=-0,13
где 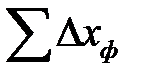 и
и 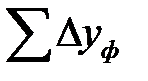 - сумма приращений координат фактическая, полученная по расчетам
- сумма приращений координат фактическая, полученная по расчетам
S  xтеор. = xк–xн; S
xтеор. = xк–xн; S  yтеор=yк–yн – разности координат конечной и начальной точек.
yтеор=yк–yн – разности координат конечной и начальной точек.
Абсолютная невязка вычисляется по формуле
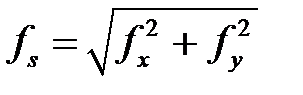 , (1.20)
, (1.20)
а затем относительную ошибку хода по формуле:
 . (1.21)
. (1.21)
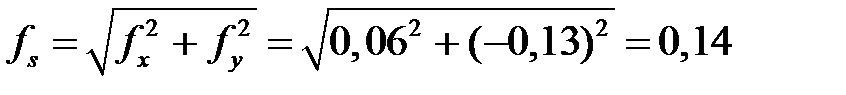
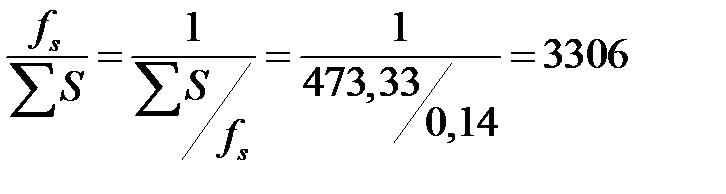
Если полученная относительная ошибка меньше допустимой, то производят уравнивание приращений координат, а если больше, то имеется ошибка в вычислениях, её следует выявить и устранить.
Поправки в приращения вводят пропорционально длинам сторон и вычисляют по формулам:
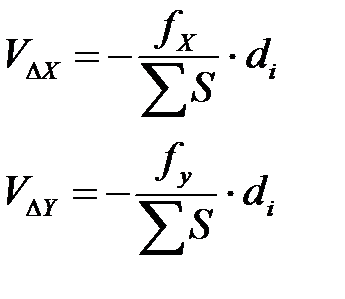 (1.22)
(1.22)
Поправки вычисляют в сантиметрах и записывают в графы 11 и 12 таблицы над вычисленными приращениями координат. Контролем правильности вычисления поправок служит равенство их суммы невязке, взятой с обратным знаком. После этого вычисляют исправленные приращения координат, складывая алгебраически вычисленное приращение и поправку. Исправленные приращения записываются в графы 13 и 14 таблицы:
Контролем правильности вычислений служит равенство суммы исправленных приращений их теоретической сумме.
Вычисление координат вершин теодолитного хода, которое является заключительным действием, и выполняется по формулам:
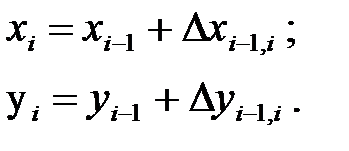 (1.23)
(1.23)
Пример
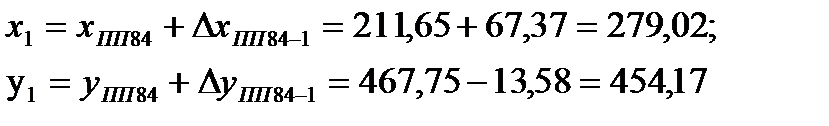
Контролем правильности вычислений служит получение координат конечной точки хода. В данном случае – получение координат пункта ПП83.
Таблица 1.4
| № вершины хода | Измеренные углы | Исправленные углы | Дирекцион- ные углы | Румбы | Горизонтальное проложение, d,м | Приращения координат | Координаты | |||||||||||||||
| ° | ' ′′ | ° | ' ′′ | ° | ' ′′ | назв | ° ' ′′ | + - | ∆x | + - | ∆y | + - | ∆ x | + - | ∆ y | + - | x | + - | y | |||
| п/п 85 | - | - | - | - | 23 37 | СВ | 11 23 37 | - | - | |||||||||||||
| п/п 84 | +0,2 48 00 | 48 20 | + | 211,65 | + | 467,75 | ||||||||||||||||
| 35 17 | СЗ | 11 24 43 | 68,74 | + | -0,01 67,38 | - | +0,02 13,60 | + | 67,37 | - | 13,58 | |||||||||||
| +0,20 12 30 | 12 50 | + | 279,02 | + | 454,17 | |||||||||||||||||
| 22 27 | СЗ | 30 37 33 | 190,36 | + | -0,02 163,81 | - | +0,05 96,97 | + | 163,79 | - | 96,92 | |||||||||||
| +0,20 10 00 | 10 20 | + | 442,81 | + | 357,25 | |||||||||||||||||
| 12 07 | СВ | 79 12 07 | 104,18 | + | -0,01 19,52 | + | +0,03 102,34 | + | 19,51 | + | 102,37 | |||||||||||
| +0,21 46 30 | 46 51 | + | 462,32 | + | 459,62 | |||||||||||||||||
| 25 16 | ЮВ | 27 34 44 | 110,05 | - | -0,02 97,55 | + | +0,03 50,95 | - | 97,57 | + | 50,98 | |||||||||||
| п/п 83 | +0,21 39 00 | 39 21 | + | 364,75 | + | 510,60 | ||||||||||||||||
| 45 55 | ЮВ | 42 14 05 | ∑=153,10 м | ∑=42,85 м | ||||||||||||||||||
| п/п 82 | - | - | - | - | ||||||||||||||||||
| Σβпр | 36 00 | 37 42 | ∑=473,33м | ∑∆хпр=153,16 м ∑∆yпр=42,72 м ∑∆хтеор= 153,10 м ∑∆yтеор= 42,85 м | ||||||||||||||||||
| Σβтеор | 37 42 | f∆х=+0,06 м f∆у=-0,13 м
fабс.= 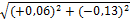 =0,14м
fотн.= =0,14м
fотн.= 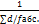 = = 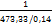 = =  ˂ ˂ 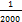 м м
| ||||||||||||||||||||
| ƒβ | -0 | 01 42 | 00 00 | |||||||||||||||||||
| ƒβ ДОП | ± | 02 24 |