Как известно, функция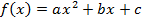 
, где 
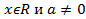, называется квадратичной, а многочлен 
, 
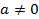часто называют квадратным трёхчленом. Рассмотрим построение графика квадратного трёхчлена.
1. Найдём вершину параболы. Её можно найти двумя способами.
1) Из школьного курса известно, что абсцисса вершины параболы находится по формуле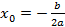 
. Чтобы найти ординату нужно в функцию вместо х подставить найденное значение абсциссы 
.
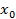2) Для квадратичной функции вершина параболы является точкой экстремума. Причём если 
то ветви параболы направлены вверх и вершина параболы является точкой минимума. При этом возможно 3 случая, связанные со знаком дискриминанта.
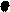
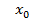
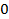
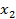
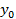
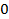
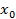
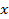
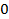
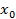
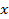
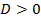
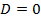
Рис.10
Если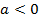 
, то ветви параболы направлены вниз и её вершина является точкой максимума. При этом возможно 3 случая.
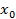
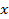
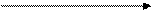
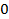
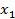
Рис.11
Поэтому, чтобы найти абсциссу вершины параболы нужно найти производную и приравнять её к нулю.
Иногда для более точного построения графика необходимо найти точки пересечения графика с осями координат.
Точки пересечения графика с осью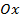 
имеют вид 
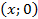, поэтому для их нахождения нужно взять 
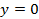, подставить в функцию и найти .
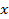Точки пересечения графика с осью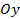 
имеют вид 
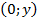, поэтому нужно взять 
, подставить в функцию и найти . Можно найти симметричную точку.
П р и м е р. Построить график функции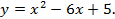 
Решение. 1)Найдём вершину параболы, для этого найдём производную и приравняем её к нулю.
. Тогда 
и 
Подставим это значение в функцию и вычислим .
.
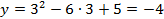Следовательно, вершина находится в точке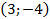 
.
2) Найдём точки пересечения параболы с осями координат.
С осью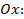 
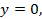тогда 
.
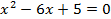Откуда получаем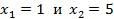 
. Точки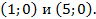 
С осью 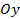: , тогда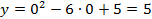 
. Точка 
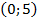и симметричная ей точка 
.
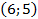По результатам исследования построим график.
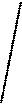
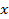
УПРАЖНЕНИЯ
Построить график функции.
1. 
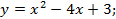
2. 
3. 
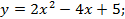
4. 
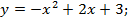
5. 
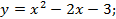
6. 
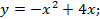
7. 
8. 
9. 
10. 
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ
ФУНКЦИИ НА ОТРЕЗКЕ
Выясним, в каких точках отрезка непрерывная функция может принять наибольшее и наименьшее значения.
Пусть функция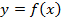 
, 
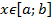, непрерывна на отрезке 
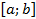, дифференцируема во всех точках этого отрезка и имеет на нём конечное число критических точек.
Очевидно, что если эта функция монотонна на отрезке 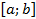, то наибольшее и наименьшее значения достигаются на концах этого отрезка (см. рис.12).
Если функция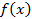 
не является монотонной, то своё наибольшее значение 
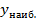на отрезке 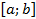она достигает либо в одной из точек максимума, либо на одном из концов этого отрезка. Точно так же наименьшее значение 
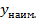на отрезке 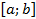функция 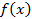достигает либо в одной из точек минимума, либо на одном из концов отрезка 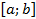(см. рис.13).
 |
 |  | ||
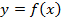
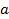
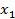
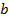
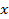
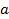
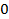
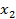
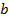
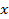
Рис.12 Рис.13
Обобщая наши наблюдения, можем составить правило нахождения наибольшего и наименьшего значений функции на отрезке.
Чтобы найти наибольшее и наименьшее значения непрерывной на отрезке 
функции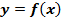 
нужно:
1. Найти критические точки, принадлежащие отрезку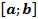 
и вычислить значения функции в этих точках.
2. Вычислить значения функции на концах отрезка 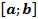, то есть найт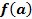и 
и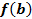 
.