Билет № 1
1.Что такое обыкновенная дробь? Запись обыкновенной дроби. Основное свойство дроби.
Привести примеры. Действия с обыкновенными дробями.
2. Параллелограмм. Определение, свойства.
3. Прямая, перпендикулярная биссектрисе угла А, пересекает его стороны в точках В и С.
Докажите, что треугольник AВС является равнобедренным.
4. Упростите выражение:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
Билет № 2
1. Что такое десятичная дробь. Действия с десятичными дробями.
2. Прямоугольник и квадрат. Определение, свойства.
3. Стороны параллелограмма равны 5 см и 11 см. Найдите его площадь, если один из углов равен 30°.
4.. Решите уравнения:
а) 2х – (6х + 1)=9; б) 4(1 – 5х) = 9 – 3(6х – 5);
в) 1,5(х – 6) = 1,4(х + 5); г) 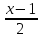 –
–  =
=  ;
;
Билет № 3
- Что такое степень с целым показателем. Свойства степени с целым показателем.
Привести примеры.
- Ромб. Определение, свойства.
- В Δ ABC угол A равен 50°, а угол B в 12 раз меньше угла C. Найдите углы B и C.
- Упростите выражение:
а) (в+с)(в-с) – в(в – 2с); б) а(а+5в) – (а–в)(а+в);
в) (х+3)2 – (х-2)(х+2); г) (с+2)(с-3) – (с-1)2;
Билет № 4
1. Что такое уравнение? Корни уравнения? Что значит решить уравнение? Алгоритм решения линейных уравнений. Привести примеры.
2. Треугольник. Площадь треугольника.
3. Найдите углы четырехугольника АВСD, если АВ ||СD, угол АВС = 138°, угол СDА = 52°.
4.. Упростите выражение:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
Билет № 5
- Квадратный корень. Свойства квадратного корня. Привести примеры.
- Площади четырёхугольников.
- В треугольнике АВС угол А = 42°, угол В = 48°. Треугольник пересечен прямой, параллельной стороне АС. Определите углы образовавшегося треугольника.
- Упростите выражение:
а) 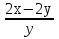 ∙
∙  ; б)
; б)  ∙
∙ 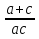 ;
;
в)  ; г)
; г) 
 ;
;
Билет № 6
- Квадратное уравнение. Алгоритм решения квадратного уравнения. Привести примеры.
- Прямоугольный треугольник. Теорема Пифагора.
- Площадь прямоугольника равна 520 м2, а отношение его сторон равно 2:5. Найдите периметр
данного прямоугольника.
|
|
- Решите систему уравнений:

Билет № 7
1. Функции  их свойства и графики
их свойства и графики
2. Признаки подобия треугольников.
3. Найдите площадь ромба со стороной 24 см и углом 120°.
4. Сравните:
а)  и 26; б) 2
и 26; б) 2 
в)  и
и  ∙
∙  ; г)
; г)  ;
;
Билет № 8
- Функция y = ax 2 + bx + c, её свойства и график.
- Окружность. Центральный угол.
- В параллелограмме АВСD биссектриса угла А пересекает продолжение ВС в точке Е. Найдите периметр параллелограмма, если ВЕ = 16 см, СЕ = 5 см.
4. Упростите выражение:
а)  ; б)
; б) 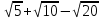 ;
;
в)  ; г)
; г)  ∙
∙  ∙
∙  - 7;
- 7;
Билет № 9
- Квадратное уравнение. Формула корней квадратного уравнения. Привести примеры.
- Пропорциональные отрезки в прямоугольном треугольнике.
- Гипотенуза прямоугольного треугольника равна 15 см. Найдите радиус окружности, описанной около треугольника.
4. Найдите значение выражения:
а)  , при х = 0,75; у = - 2,25; z = - 0,6;
, при х = 0,75; у = - 2,25; z = - 0,6;
б)  , при a = 1,2; x = - 0,3;
, при a = 1,2; x = - 0,3;
в)  , при х = - 7; у = 3;
, при х = - 7; у = 3;
г)  ; при m =2; n = -
; при m =2; n = -  .
.
Билет № 10
- Рациональные уравнения, алгоритм решения рационального уравнения, проверка корней уравнения, посторонние корни. Привести примеры.
- Синус, косинус и тангенс острого угла прямоугольного треугольника.
- В окружности проведены хорды АВ || СD и АЕ || FD. Докажите, что хорды FВ и СЕ параллельны.
- Решить уравнения: а) 2х2+3х+1=0 б) 4х2+4х+1=0 в) 4а2-5а+9=0.
Билет № 11
- Теорема Виета. Разложение квадратного трехчлена на множители.
- Окружность. Вписанный угол.
- Найдите периметр ромба, площадь которого равна 48 см2, а острый угол равен 30°.
- Из города в село, расстояние до которого равно 120 км, выехал велосипедист. Через 6 часов вслед за ним выехал мотоциклист, скорость которого на 10 км/ч больше скорости велосипедиста. Определите скорости велосипедиста и мотоциклиста, если в село они прибыли одновременно.
Билет № 12
|
|
- Неравенства. Решение линейных и квадратных неравенств. Привести примеры.
- Признаки параллельности прямых.
- Хорда окружности пересекает ее диаметр под углом 30° и делится им на части, равные 12 см и 6 см. Найдите расстояние от середины хорды до диаметра.
- Два слесаря, работая совместно, могут выполнить задание на 8 дней быстрее, чем один первый слесарь и на 18 дней быстрее, чем один второй. Сколько дней потребуется слесарям на совместное выполнение задания?
Билет № 13.
- Общие понятия о действительных числах.
- Трапеция и её свойства. Формула площади. Решение задачи.
3. Площадь трапеции равна 288 см2, а основания относятся как 4:5, высота - 3,2 дм. Вычислите основания.
- Решите квадратное неравенство: -25х2-30х-9 ≤ 0.
Билет № 14.
- Определение арифметического квадратного корня.
- Теорема Фалеса. Применение теоремы к решению практической задач.
3.Задача: Разделите отрезок АВ на 5 равных частей, применив теорему Фалеса.
4.Решите неравенство методом интервалов:  .
.
Билет № 15.
- Свойства арифметического квадратного корня.
- Параллелограмм и его свойства. Формулы площади для параллелограмма. Решение задачи.
3.Задача: Найдите острый угол параллелограмма, стороны которого равны 14 м и 8 м, а площадь равна 56 м2.
4.Разложите квадратный трёхчлен на множители: 6х2-5х+1.
|
|
Билет № 16.
- Преобразование выражений, содержащих квадратные корни.
- Ромб и его свойства. Формулы площадей для ромба. Решение задачи.
3.Задача: Углы, образованные стороной ромба и его диагоналями, относятся как 2:7. Найдите его углы.
- Сократите дробь:
 .
.
Билет № 17.
- Функция
 , её свойства и график.
, её свойства и график. - Прямоугольник, квадрат и их свойства. Формулы площадей. Решение задачи.
3.Задача: Найдите стороны прямоугольника, зная, что отношение его сторон равно 5:7, а площадь равна 140 дм2.
4.Сократите дробь:  .
.
Билет № 18.
- Освобождение дроби от иррациональности в знаменателе дроби.
- Треугольник и его виды. Формулы площадей для треугольника. Решение задачи.
3.Задачи: Найдите наименьшую сторону треугольника, у которого стороны равны 25 м, 29 м, 36 м.
4.Найдите значение выражения:  .
.
Билет № 19.
- Квадратное уравнение. Виды квадратных уравнений.
- Средние линии треугольника и трапеции и их виды. Решение задачи.
3.Задача: Средняя линия трапеции равна 10 дм и делится её диагональю на два отрезка с разностью, равной 4 м. Найдите длины оснований трапеции.
4.Используя определение квадратного корня, решите уравнение:  .
.
Билет № 20.
- Формулы корней квадратных уравнений.
- Замечательные точки треугольника. Решение практической задачи.
3.Задача: Найдите центр тяжести и ортоцентр в треугольнике АВС.)
3. Вычислите:  .
.
Билет № 21.
- Теорема Виета.
- Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника. Решение задачи.
3. Задача: Найдите синусы, косинусы, тангенсы и котангенсы углов А и В треугольника АВС с прямым углом С, если ВС=21, АС=20, АВ=29.
- Решите уравнение: (5х+1)2 = 400.
Билет № 22.
- Рациональные уравнения.
- Теорема Пифагора. Решение задачи.
3.Задача: Сторона ромба равна 13 дм, а одна из диагоналей равна - 10 дм. Найдите длину второй диагонали.
4.Освободитесь от иррациональности в знаменателе дроби: 
 .
.
Билет № 23.
- Уравнения, приводящиеся к квадратным.
- Основные тригонометрические тождества. Решение тригонометрического выражения.
3.Найдите синус, тангенс и котангенс, если cos α = 0,8.)
4.Сократите дробь:  .
.
Билет № 24.
- Решение задач с помощью квадратных уравнений.
- Значения тригонометрических выражений основных углов. Вычисление тригонометрического выражения.
3.Вычислите: cos230°·sin230° - cos260°- sin260°+ sin245°+ cos245°.)
- Решите уравнение:
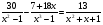 .
.
Билет № 25.
- Квадратный трехчлен. Разложение квадратного трехчлена на множители.
- Координаты точки на плоскости. Координаты середины отрезка. Расстояние между двумя точками. Решение задачи.
3.Задача: Найдите координаты точки С, лежащей на середине отрезка АВ и длину отрезка АВ, если А(-1;-7), В(-4;3).)
4.Упростите выражение:  .
.
Билет № 25.
- Определение квадратичной функции. Функции y=ax2+n и y=a(x-m)2.
- Уравнение окружности. Решение задачи.
3.Задача: Составьте уравнение окружности с центром в точке С(2; -1) и радиусом равным 2. Выясните, принадлежит ли точка А(2; -3) этой окружности.
4.Решите уравнение: х4-13х2+36 = 0.
Билет № 26.
- График функции у=ах2+вх+с.
- Уравнение прямой. Решение задачи.
3.Задача: Составьте уравнение прямой, проходящей через точки А(9; -3) и В(-6; 1).)
4.Решите уравнение: (х2-8)2+3,5(х2-8)-2=0.
Билет № 27.
- Квадратное неравенство. Решение квадратного неравенства с помощью графика квадратичной функции.
- Понятие о площади фигуры. Свойства площади.
- Решите уравнение, используя теорему Виета: х2+9х-22=0.
Билет № 28.
- Метод интервалов.
- Формулы площадей для плоских фигур. Решение задачи.
3.Задача: Диагонали равнобедренной трапеции взаимно перпендикулярны. Основания равны 24 см и 40 см. Вычислите её площадь.
4.Решите уравнение: 3х2+10х+7=0