Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами - массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа.
Основное уравнение МКТ идеального газа имеет вид: 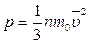 , где т0 - масса одной молекулы газа
, где т0 - масса одной молекулы газа  - концентрация молекул
- концентрация молекул  - среднее значение квадрата скорости молекул. Коэффициент 1/3 предопределен трехмерностью пространства - тем, что во время хаотического движения молекул все три направления равноправные.
- среднее значение квадрата скорости молекул. Коэффициент 1/3 предопределен трехмерностью пространства - тем, что во время хаотического движения молекул все три направления равноправные.
Проанализируем выражение  :
:  .
.
Следовательно, основное уравнение МКТ можно записать в виде: 
Связь давления со средней кинетической энергией молекул.
Учитывая, что средняя кинетическая энергия поступательного движения молекулы  основное уравнение МКТ можно записать в виде:
основное уравнение МКТ можно записать в виде:  .
.
2. Обобщение знаний.
Заполнить обобщающую таблицу:
| Название | Формула |
| Молярная масса | |
| Масса одной молекулы | |
| Количество вещества | |
| Количество молекул | |
| Масса вещества | |
| Концентрация молекул | |
| Плотность | |
| Основное уравнение МКТ | |
| Средняя кинетическая энергия движения молекул | |
| Средняя скорость движения молекул | |
| Число Авогадро | |
| Стала Больцмана | |
| Универсальная газовая стала |
3. Решение задач.
Средний уровень
№ 1.
Найти среднюю квадратичную скорость молекул газа, который имеет плотность 1,8 кг/м3, если его давление равняется 152 кПа. (Ответ: 500м/с)
Достаточный уровень:
№ 3.
Определить давление, при котором 1 м3 газу при температуре 60 С содержит 2,4 1026 молекул
Уравнение состояния.
Величинами, которые определяют состояние газа, являются: давление р, под которым находится газ, его температура Т и объем V, который занимает определенная масса газа. Их называют параметрами состояния. Не перечислены три величины независимыми: каждая из них является функцией двух других. Уравнение, которое связывает все три параметра - давление, объем и температуру газа для данной его массы, называется уравнением состояния.
Как известно  . С учетом того, что
. С учетом того, что  имеем:
имеем: 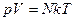 . Это уравнение, в котором задействованы все три параметра состояния, и является уравнением состояния идеального газа.
. Это уравнение, в котором задействованы все три параметра состояния, и является уравнением состояния идеального газа.
Поскольку,  то
то  .
.
Произведение универсальных констант, является универсальным газовой постоянной: 
Тогда 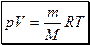 . Поданное в таком виде уравнение состояния идеального газа называется уравнением Менделеева-Клапейрона.
. Поданное в таком виде уравнение состояния идеального газа называется уравнением Менделеева-Клапейрона.
Уравнение Клапейрона.
Основное содержание уравнения состояния идеального газа можно выразить таким способом:
 .
.
Если индексом 1 обозначить параметры, которые принадлежат к первому состоянию, а индексом 2 - ко второму, то для данной массы газа имеем:
 . Уравнение состояния в такой форме называется уравнением Клапейрона.
. Уравнение состояния в такой форме называется уравнением Клапейрона.
Работа газа при изобарном расширению определяется формулой:
A=p ∆V
Уравнение состояния идеального газа позволяет описать, что происходит с газом при любых изменениях всех его параметров. Однако, многие процессы в газах, которые происходят в природе или осуществляются при участии техники, допустимо рассматривать (приблизительно) как процессы, в которых один из макропараметров остается неизменным.
Изопроцессами называются процессы, которые протекают в системе с неизменной массой при постоянном значении одном из параметров состояния системы.
Изопроцессы.
1) Изотермический процесс - процесс, который происходит при неизменной температуре.
 Запишем уравнение Клапейрона:
Запишем уравнение Клапейрона:  .
.
Поскольку температура не изменяется, то Т1=Т2. Тогда р1V1=p2V2, или  . Это соотношение было выявлено экспериментально во второй половине XVII ст. английским ученым Р. Бойлем и французским ученым Е. Мариоттом, потому его называют законом Бойля — Мариотта.
. Это соотношение было выявлено экспериментально во второй половине XVII ст. английским ученым Р. Бойлем и французским ученым Е. Мариоттом, потому его называют законом Бойля — Мариотта.
!! Для газа данной массы, произведение давления газа на его объем остается неизменным, если температура не изменяется.
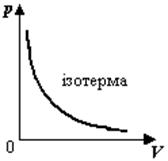
График зависимости р(V) при Т = const называют изотермой.
2) 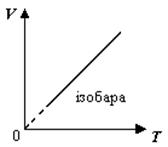 Изобарный процесс - процесс, который происходит при неизменном давлении.
Изобарный процесс - процесс, который происходит при неизменном давлении.
Из уравнения Клапейрона получаем:  . Поскольку р1=р2, то
. Поскольку р1=р2, то 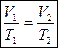 - закон Гей-Люссака (в честь французского ученого, который открыл его экспериментально в 1802 году.)
- закон Гей-Люссака (в честь французского ученого, который открыл его экспериментально в 1802 году.)
!! Для газа данной массы, отношения объема газа к абсолютной температуре остается неизменным при неизменном давлении.
График зависимости V(Т) при р = const называют изобарой (рис. 2).
3)  Изохорный процесс - процесс, который происходит при неизменном объеме.
Изохорный процесс - процесс, который происходит при неизменном объеме.
Запишем уравнение Клапейрона:  . Поскольку объем не изменяется, то есть, V1=V2, то
. Поскольку объем не изменяется, то есть, V1=V2, то  - закон Шарля
- закон Шарля
!! Для газа данной массы, отношения давления газа к абсолютной температуре остается неизменным, если объем не изменяется.
График зависимости р(Т) при V = const называют изохорой(рис. 3).
4. Решение задач.
№ 1.
Газ, который находится под давлением 972 кПа, при температуре 470С занимает объем 800 л. Каким станет давление той же массы газа, если при температуре 285 К он будет занимать объем 855 л. (Ответ: 810 кПа)
№ 2.
 Охарактеризовать процессы, которые происходят с идеальным газом. Построить графику в других координатах:
Охарактеризовать процессы, которые происходят с идеальным газом. Построить графику в других координатах: