Тема 1. Функция
Октября 2018
Понятие функции и ее аргумента
Пусть X и Y - произвольные множества. Говорят, что на Х задана функция f, если каждому элементу х множества Х поставлен в соответствие единственный элемент у множества Y. Закон соответствия обычно обозначается f: Х ®Y, y=f(x).
х называется аргументом функции у.
Областью определения функции называют числовое множество Х и обозначают D(f), областью значений функции называют множество Y, состоящее из значений, которые принимает функция при подстановке чисел из множества Х, и обозначают E(f).
Способы задания функций
· Табличный способ.
Пример. Мы знаем значения функции для 1, 2 и 4.
| х | y |
| ? | |
Можем предположить, что это функция 
и для x=3 предположить значение 9. Но это необязательно так. Например, функцией может оказаться многочлен третьей степени: 
*Как найти такой многочлен, если мы знаем его степень? – Метод неопределенных коэффициентов 
. При использовании этого метода становится очевидно, что квадратный трехчлен, проходящий через заданные три точки определяется однозначно, а вот уже для многочлена третьей степени существует бесконечное множество вариантов
· Графический способ.
Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
· Аналитический способ – задание формулой y = f(x) или F(x,y)=0. В том числе можно выделить параметрический способ задания функции, когда используется параметр, через который выражаются х и y по отдельности.
Пример. 
Чтобы перейти от параметрической формы к явной аналитической, необходимо исключить параметр из системы:
|
|
Получаем прямую
· Словесный способ.
Элементарные функции
линейная (
),
квадратичная (
),
степенная (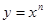
, где n целое число, не равно 1),
иррациональная (степенная функций с рациональными показателями)
тригонометрические (y=sin x, y=cos x, y=tg x, y=ctg x),
обратные тригонометрические (y=arcsinx, y=arccosx, y=arctgx, y=arcctgx).
показательная (
,где a больше 0 и не равно 1),
логарифмическая (
, где a больше 0 и не равно 1).
Функциональные уравнения
Это такие уравнения, где неизвестной является функция.
Плоские множества
Дана исходная функция y=f(x) (то же самое работает для F(x,y)=0).
Ее график (геометрический образ) задает некоторую границу, можно говорить, что эту границу также задает ее уравнение y=f(x) (F(x,y)=0) – точки, координаты которых удовлетворяют уравнению составляют эту границу.
Если рассмотреть неравенство y≥f(x) (F(x,y) ≥0), оно будет задавать область на координатной плоскости, при этом нестрогость знака означает, что граница включена в образ, а строгость – что все ее точки выколоты (обычно обозначается пунктиром).
Пример. 
- круг единичного радиуса
Преобразование графиков функций и других геометрических образов
Дана исходная функция y=f(x) (то же самое работает для F(x,y)=0)
1. y=f(x)+A – график функции смещается на А единиц вверх (если А >0) или вниз (если А <0) вдоль оси Oy
2. y=f(x-A) – график функции смещается на А единиц вправо (если А >0) или влево (если А <0) вдоль оси Ox
3. y=-f(x) – график функции симметрично отображается относительно оси Ох
4. y=f(-x) – график функции симметрично отображается относительно оси Oy
5. y=|f(x)| - часть графика, находившаяся выше оси Ох, остается неизменной, а часть графика, находившаяся ниже этой оси, симметрично отображается относительно Ох
|
|
6. y=f(|x|) – часть графика, находившаяся правее оси Оy, остается неизменной и симметрично отражается влево относительно оси Oy.
7. y=kf(x), где k >0 – происходит растяжение графика функции вдоль оси Oy относительно оси Ох (если k >1)/ сжатие (если k <1)
8. y=f(kx), где k >0 – сжатие вдоль оси Ох относительно Оy (если k >1)/ растяжение (если k <1)