Научный реферат по статье «Симлектические нильмногообразия и приложения» Виктора Матвеевича Бухштабера.
Объём работы данной статьи составляет 65 страниц, автор ссылается на 12 источников, в статье имеется несколько таблиц.
Ключевые слова: симплектические нильмногообразия, башня расслоений, симплектическая структура, нильпотентная группа, группа Ли, кокомпактные решётки, левоинвариантные дифференциальные операторы, дифференциальная градуированная алгебра.
Цель данной работы была представить башню расслоений 
и показать способ, по которому можно приблизительно понять, что такое такое 
, рассмотреть дифференциально-алгебраические и алгебро-топологические результаты и написать нерешённые проблемы, касающиеся этих многообразий.
Работа не имеет аналогов и является исключительной по данной тематике, была опубликована в декабре 2011 года.
Статья содержит 26 разделов:
1. Введение.
2. Группы полиномиальных преобразований. Пример.
3. Структура нильпотентной группы в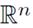 
.
4. Каноническое матричное представление. Пример.
5. Деформация к стандартной групповой структуре. Пример
6. Кокомпактные решётки.
7. Нильмногообразия.
8. Левоинвариантные дифференциальные операторы. Пример.
9. Алгебра левоинвариантных операторов. Пример.
10. Кольцо когомологий дифференциальной градуированной алгебры. Пример.
11. Дифференциальная градуированная алгебра левоинвариантных дифференциальных форм на нильмногообразии. Пример.
12. Биградуированные когомологии кольца нильмногообразий. Пример.
13. 10 дифференциальных подкомплексов.
14. Образующие двойственности Пуанкаре.
15. Торические расслоения.
16. Симплектические нильмногообразия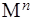 
.
17. Целостность симплектической формы. Пример.
18. Неформальные нильмногообразия. Теорема.
19. Универсальные свойства .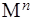
20. Клеточное подразделение .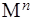
21. Формула Хопфа целочисленных гомологий. Примеры. Следствие.
22. Проблема классификации последовательности гладких многообразий.
23. Ссылки на другие источники.
24. Приложение. Произведение Масси. Лемма.
25. Бесконечномерная алгебра векторых полей на линии.
26. Группа Гейзенберга.
В 1 разделе читателя знакомят с понятием башни расслоений, как она определяется,обсуждается чем является 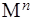, какая задана на нём структура.
Во 2 разделе строится группа полиномиальных преобразований. Вводим понятие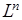 
и рассматриваем её как n-мерную группу полиномиальных преобразований вещественной прямой с умножением *. Даётся наглядный пример для n=4.
В 3 разделе рассматриваем в 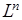структуру нильпотентной группы с верхним центральным рядом.
В 4 разделе обсуждаем, что левое умножение * имеет каноническое матричное представление в группе нижнетреугольных матриц (n+1)*(n+1) с единицами на главной диагонали. Рассматривается пример при n=4.
В 5 разделе умножение * представляем как x*y=x+y+A(x)y. Находим для n=4 данную матрицу А(х).
В 6 разделе рассматриваем каноническую решётку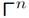 
с верхним центральном рядом. Делаем вывод, что на кокомпактна.
В 7 разделе определяем непосредственно нильмногообразие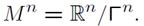 
Строим индуцированный ряд 
с расслоением 
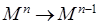со слоем 
.
В 8 разделе фиксируем кольцо многочленов как кольцо функций и рассматриваем левоинвариантные дифференциальные операторы.
В 9 разделе рассматриваем алгебру левоинвариантных операторов. Считаем коммутаторы этих операторов. Рассматриваем частные случаи при n=3 и n=4.
В 10 разделе вводим понятие дифференциальной градуированной алгебры и строим её кольцо. Рассматриваем пример.
В 11 разделе выписываем уравнение Маурера-Картана для нашего случая.
В 12 разделе рассматриваем биградуированные когомологии кольца. Приводим пример для n=4.
В 13 разделе выписываем таблицу 10 дифференциальных подкомплексов.
В 14 разделе выписываются образующие двойственности Пуанкаре для размерностей от 0 до 4.
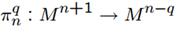В 15 разделе приводится пример двух точных последовательностей, которые дают гладкое расслоение
со слоем тора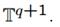 
В 16 разделе вводится понятие симлектического нильмногообразия и симплектической формы.
В 17 разделе обсуждается целостность симплектической формы.
В 18 разделе вводится понятие неформального симплектического комплекса и нильмногообразия. Выписывается Теорема Джонсона Риса 1989 года:
Если G нильпотентная группа Ли и Г 
G – дискретная кокомпактная подгруппа, то G/Г – формальная тогда и только тогда, когда G абелева.
Выписывается теорема Бабенко и Тайманова 1999 года:
Для m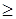 
2 и N 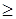2m+1 симплектическое многообразие 
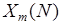односвязно и неформально.
В 19 разделе рассказывается про универсальные свойства 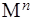, выписываются основные соотношения когомологий нильмногообразий.
В 20 разделе рассматриваем клеточное подразделение 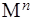, строим точные последовательности, выясняем что группа 
имеет только 2-кручения.
В 21 разделе приводится формула Хопфа целочисленных когомологий. Рассматриваются примеры для n=3, n=4. Делаются вывод:
Каждый элемент 
, n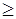 
2, реализуется гладким отображением
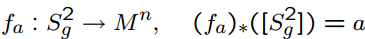
для некоторого g.
В 22 разделе мы узнаём о проблеме:
Для башни расслоений вычислить кольцо когомологий 
для 
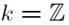и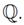 
Д. В. Миллионщиков получил результаты на числа Бетти 
для многообразий 
, определённых групп 
.
Его подход основан на расчётах Гончаровой беконечных алгебр Ли когомологий.
Для таких многообразий он доказал, что
Миллионщиком использовал некоторые комбинаторные аргументы и теорему Гончаровой, чтобы набросать доказательство утверждения 
для n>3q+2, где 
- это (q+2)-ое число Фибоначчи
Однако никакого подробного доказательства этого утверждения не появилось до сих пор. Недавно он предложил рассмотреть последнее утверждение в качестве гипотезы. Используя компьютер, Миллионщиков посчитал числа Бетти для
n 
30.
В 23 разделе автор даёт ссылки на статьи, схожие по тематике.
В 24 разделе вводится понятие произведения Масси.
В 25 разделе обсуждаем теорему Гончарова 1973 года:
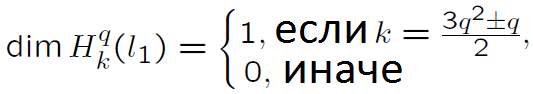
В 26 разделе автор рассматривает группу Гейзенберга относительно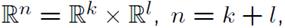 
, пишет формулу для операции умножения в этой группе, рассматривает группу при k=2,l=1.