Контрольная работа
На тему
«Статистическая обработка результатов измерений»
по дисциплине
«Метрология, стандартизация и сертификация в инфокоммуникациях»
Задание №2
Выполнил:
Факультет: ИнЭТиП
Курс:3
Специальность б-ИКТСипу31
Шифр №182883
Гезь Виктор Алексеевич
Проверил: доцент, к.т.н.,
доцент Скворцов А. А.
Саратов 2021
Задание на контрольную работу
Провести статистическую обработку ряда из 28 измерений, воспользовавшись данными таблицы. Оценить наличие результатов, содержащих грубые погрешности. Результаты расчетов свести в приведенную ниже таблицу.
Таблица 1. Данные для статистической обработки ряда из 28 измерений
| № измерения | 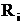 , Ом , Ом
| 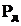
| 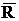
| 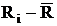
| 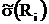
| 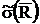
| 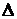
|
| 0,99997 | |||||||
Содержание:
Введение…………………………………………………………...…4
Основные теоретические сведения. 4
Расчет: 11
Заключение. 14
Список использованных источников: 15
Введение
Измерения — один из важнейших путей познания природы человеком. Они играют огромную роль в современном обществе. Наука и промышленность не могут существовать без измерений. Практически нет ни одной сферы деятельности человека, где бы интенсивно не использовались результаты измерений, испытаний и контроля.
|
|
Одной из причин важности измерений является их значимость. Основа любой формы управления, анализа, прогнозирования, контроля или регулирования — достоверная исходная информация, которая может быть получена лишь путем измерения требуемых физических величин, параметров и показателей. Только высокая и гарантированная точность результатов измерений обеспечивает правильность принимаемых решений.
Целью данной работы является произведение статистической обработки конкретно ряда измерений.
Для достижения поставленной цели предстоит изучить сведения о обработке результатов измерений.
Целью работы: освоение методики статистической обработки результатов прямых равноточных многократных измерений сопротивления резистора, предназначенного для аттенюатора.
Основные теоретические сведения
Абсолютная погрешность (ΔX, Δ) – отклонение результата измерения от истинного значения величины. Выражается в тех же единицах измерения, что и измеряемая величина.
ΔX=Xизм-Xист
Предельная погрешность (разновидность абсолютной, (ΔmX)) – это абсолютная погрешность, больше которой в данном измерительном эксперименте не может быть.
Абсолютная погрешность характеризует величину и знак полученной погрешности, но не определяет качество самого измерения.
Относительная погрешность - отношение абсолютной погрешности к тому значению, которое принимается за истинное. Выражается в долях или процентах.
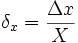
Характеристикой качества измерений является точность отражающая меру близости измеряемых выражений к истинности.
|
|
Коэффициент погрешности:
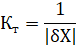
Приведенная погрешность (разновидность относительной погрешности) – отношение абсолютной погрешности к некоторому нормирующему значению.
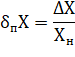
Систематическая погрешность (Δс) – это соответствующая погрешность измерений, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины в тех же условиях.
В основу положен характер изменения во времени:
· Постоянная Δс
· Переменная Δс
Постоянная Δс – длительное время сохраняет свое значение (например в течении времени измерения).
Переменная Δс – изменяется во время процесса измерения.
· Прогрессирующая
· Периодическая
· Изменяющаяся по сложному непериодическому закону
Прогрессирующая Δс – монотонно возрастающая или убывающая Δс (как правило, изменяется по линейному закону).
Периодическая Δс – значение которой является периодическая функция во времени.
Изменяющаяся по сложному непериодическому закону – возникает в следствии действия нескольких систематических погрешностей.
Оценка и исключение систематической погрешности.
Систематическая погрешность (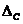 ) может быть связана с каждым из элементов процесса измерения: несовершенством модели объекта измерения, несовершенством метода, изменением внешних условий и т.д.
) может быть связана с каждым из элементов процесса измерения: несовершенством модели объекта измерения, несовершенством метода, изменением внешних условий и т.д.
Существуют простейшие способы обнаружения и исключения 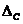 :
:
- Исключение 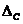 при измерении путём применения соответствующих методов и приёмов, например, метода замещений, метода компенсации
при измерении путём применения соответствующих методов и приёмов, например, метода замещений, метода компенсации 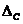 по закону двух измерений, когда
по закону двух измерений, когда 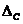 входит с разными знаками и др. Эти методы позволяют исключить
входит с разными знаками и др. Эти методы позволяют исключить 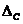 , обнаружение которой представляет наибольшие трудности, непосредственно в процессе измерения, а не путём обработки результатов.
, обнаружение которой представляет наибольшие трудности, непосредственно в процессе измерения, а не путём обработки результатов.
|
|
- Оценка 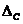 путём применения более точного метода и средства измерения (СРИ). - - Обнаружение
путём применения более точного метода и средства измерения (СРИ). - - Обнаружение 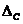 при измерениях с многократными наблюдениями одной физической величины двумя независимыми методами.
при измерениях с многократными наблюдениями одной физической величины двумя независимыми методами.
- Оценка 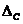 расчётным путём:
расчётным путём:
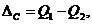
где  - значение измеряемой величины с учётом влияющего фактора, а
- значение измеряемой величины с учётом влияющего фактора, а 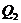 - значение измеряемой величины при его отсутствии.
- значение измеряемой величины при его отсутствии.
- Исключение 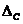 путём введения поправки. Критерием целесообразности её введения является интервал суммарной погрешности измерений.
путём введения поправки. Критерием целесообразности её введения является интервал суммарной погрешности измерений.
Для уменьшения 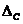 в сложном приборе предусматривается возможность его калибровки с помощью внешнего или внутреннего источника калибровочного сигнала с известными параметрами.
в сложном приборе предусматривается возможность его калибровки с помощью внешнего или внутреннего источника калибровочного сигнала с известными параметрами.
Случайная погрешность (Δ) - составляющая погрешность измерений, при повторных измерениях одной и той же величины и в тех же условиях без видимой закономерности.
Грубая погрешность – существенно превышающая погрешность (значение) оправданная условиями измерения, свойствами измерений и квалификацией оператора.
Возникает в следствии резкого, кратковременного воздействия. Грубая погрешность определяется статистическими методами и исключается из дальнейшего измерения.
Промах – грубая погрешность в следствии неправильного действия оператора.
Оценка и исключение случайной погрешности.
Случайная погрешность (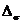 ) как случайная величина характеризуется плотность распределения вероятностей:
) как случайная величина характеризуется плотность распределения вероятностей:
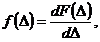
| (1) |
где 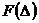 - функция распределения.
- функция распределения.
Вероятность (Р) нахождения 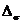 в заданном интервале
в заданном интервале 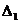 и
и 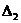 :
:
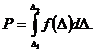
| (2) |
Закономерность изменения 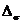 устанавливается при многократных наблюдениях ее значений и статистической обработке результатов наблюдений.
устанавливается при многократных наблюдениях ее значений и статистической обработке результатов наблюдений.
В практике электрорадиоизмерений чаще всего имеют дело с нормальным и равномерным распределением 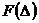 . Функция распределения по нормальному закону:
. Функция распределения по нормальному закону:
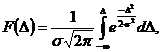
| (3) |
где 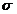 - среднее квадратическое отклонение (СКО).
- среднее квадратическое отклонение (СКО).
Плотность вероятности:
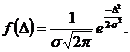
| (4) |
Рассмотрим процедуру статистического измерения некоторой величины, истинное значение которой 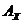 .После проведения
.После проведения 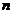 наблюдений пусть получен ряд случайных значений измеряемой величины
наблюдений пусть получен ряд случайных значений измеряемой величины 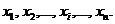 .В каждой
.В каждой 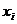 абсолютная погрешность
абсолютная погрешность 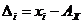 .Определить
.Определить 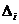 невозможно, так как неизвестна
невозможно, так как неизвестна 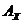 .
.
За оценку математического ожидания (истинного значения) принимают среднее арифметическое значение:
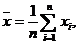
| (5) |
которое называют действительным значением А измеряемой величины 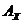 . Теперь можно вычислить абсолютное отклонение
. Теперь можно вычислить абсолютное отклонение 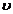 каждого результата наблюдений относительно среднего значения:
каждого результата наблюдений относительно среднего значения:
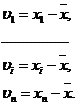
| (6) |
Для контроля правильности вычислений можно использовать свойства отклонений результатов наблюдений от среднего арифметического:
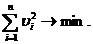
| (7) |
Оценка СКО абсолютных отклонений 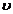 каждого из однократных наблюдений:
каждого из однократных наблюдений:
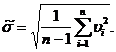
| (8) |
Точность результата n измерений характеризуется оценкой СКО среднего арифметического значения:
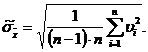
| (9) |
С увеличением n точность измерений возрастает.
В результате n наблюдений измерений величины 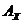 получается оценка ее действительного значения А, равного среднему арифметическому. Эта оценка – также случайная величина, ее СКО определяется по формуле (9), то есть результатов измерения содержит неопределенность. Возникает вопрос о том, в каких пределах может изменяться А при статистических измерениях
получается оценка ее действительного значения А, равного среднему арифметическому. Эта оценка – также случайная величина, ее СКО определяется по формуле (9), то есть результатов измерения содержит неопределенность. Возникает вопрос о том, в каких пределах может изменяться А при статистических измерениях 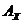 в одних и тех же условиях, то есть необходимо определить так называемый доверительный интервал и заданную (доверительную) вероятность. Истинное значение
в одних и тех же условиях, то есть необходимо определить так называемый доверительный интервал и заданную (доверительную) вероятность. Истинное значение 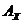 заключено в пределах доверительного интервала с некоторой вероятностью
заключено в пределах доверительного интервала с некоторой вероятностью 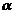 . В зависимости от целей измерения доверительную вероятность устанавливают равной 0,9...0,99.
. В зависимости от целей измерения доверительную вероятность устанавливают равной 0,9...0,99.
Для числа наблюдений 2<n<20 доверительный интервал определяется через коэффициент 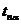 ,закон изменения которого определяется распределением Стьюдента и нормированной случайной величиной:
,закон изменения которого определяется распределением Стьюдента и нормированной случайной величиной:
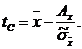
| (10) |
По причинам источника возникновения погрешности делятся:
· Объективные, не связанные с оператором (инструментальные, методические, внешние погрешности).
· Субъективные, обусловленные неправильными действиями оператора.
Методическая погрешность – составляющая, обусловленная несовершенством метода измерения, некорректностью алгоритмов и формул, несоответствием моделей объекта измерений, той, что правильно описывает его свойства. А так же из-за влияния средства измерения.
Инструментальная погрешность – составляющая погрешность соответствующая погрешность измерений, обусловленная несовершенством средств измерений их свойствам.
· Схемная
· Технологическая
· Эксплуатационная
Внешняя погрешность – составляющая, связанная с отклонением одной или нескольких величин влияющих на значение.
По условиям эксплуатации различают:
· Основная погрешность – погрешность средства измерения, оговоренная в документах.
· Дополнительная погрешность – выход одной из влияющих величин за пределы нормального значения.
По характеру поведения измеряемой величины во время измерения:
· Статистическая погрешность – возникает при измерении установившегося значения измеряемой величины.
· Динамическая погрешность – измеряемая величина изменяется во времени и требуется установить закон ее изменения во времени
Расчет:
Первым делом необходимо определить математическое ожидание заданной величины (среднее арифметическое): по формуле [2]:
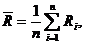
где n – количество измерений; 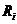 - показание i-го измерения.
- показание i-го измерения.
Подставляем известные данные и получаем:
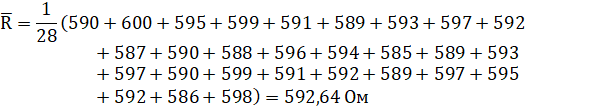
Определим абсолютную погрешность (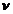 ) как разницу между значениями i-го измерения и средним арифметическим ряда из n измерений:
) как разницу между значениями i-го измерения и средним арифметическим ряда из n измерений:
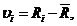
где 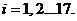
Определим абсолютную погрешность первого измерения:
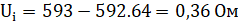
Остальные вычисления производятся аналогично (табл. 1, столбик 5).
Среднеквадратическое отклонение (СКО) погрешности i-го измерения, характеризующее точность измерения:
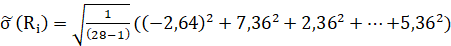 =5,410753 Ом
=5,410753 Ом
Определим наличие промахов, используя критерий 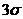 . Наибольшее по модулю значение абсолютной погрешности, составляет 7,64 Ом
. Наибольшее по модулю значение абсолютной погрешности, составляет 7,64 Ом
Очевидно, что:
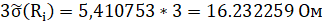
Тогда
7,64 Ом < 16.232259 Ом.
Можно сделать вывод, что по критерию 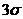 ряд экспериментально определенных значений не имеет грубых погрешностей.
ряд экспериментально определенных значений не имеет грубых погрешностей.
Точность результата 28 измерений характеризуется оценкой СКО среднего арифметического значения:
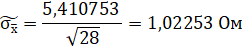
Доверительный интервал определим по доверительной вероятности (РД=0,99997). При помощи таблицы определим коэффициента Стьюдента
tcт=4,20
Границы доверительного интервала:
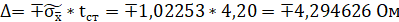
Получаем, величину измеряемого сопротивления с учётом погрешности:
R=592.64  Ом
Ом
Таблица 2.Результаты расчетов
| № измерения | 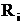 , Ом , Ом
| 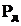
| 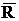
| 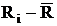
| 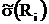
| 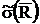
| 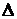
|
| 0,99997 | 592.64 | -2,64 | 5,410753 | 1,02253 | 4,294626 | ||
| 7,36 | |||||||
| 2,36 | |||||||
| 6,36 | |||||||
| -1,64 | |||||||
| -3,64 | |||||||
| 0,36 | |||||||
| 4,36 | |||||||
| 0,64 | |||||||
| -5,64 | |||||||
| -2,64 | |||||||
| -4,64 | |||||||
| 3,36 | |||||||
| 1,36 | |||||||
| -7,64 | |||||||
| -3,64 | |||||||
| 0,36 | |||||||
| 4,36 | |||||||
| -2,64 | |||||||
| 6,36 | |||||||
| -1,64 | |||||||
| -0,64 | |||||||
| -3,64 | |||||||
| 4,36 | |||||||
| 2,36 | |||||||
| -0,64 | |||||||
| -6,64 | |||||||
| 5,36 |
Заключение
В ходе работы была проведена статистическая обработка ряда из 28 измерений. Результаты расчетов были сведены в таблицу 2. Я приобрел навыки расчета погрешностей многократных равноточных измерений.
При обработке заданного ряда экспериментальных данных, установлено, что заданный ряд не имеет грубых погрешностей, величина границ доверительного интервала с вероятностью 0,99997 составляет ±4,294626 Ом, математическое ожидание измеряемой величины составляет 592.64Ом.
Список использованных источников:
1. Боридько С.И. Дементьев Н.В. «Метрология и электрорадиоизмерения в телекоммуникационных системах» 2007
2. Радкевич Я.М., Схиртладзе А.Г., Лактионов Б.И. «Метрология, стандартизация и сертификация», Москва, 2003
3. Ушаков И.Е, «Прикладная метрология. Учебник для вузов» СЗТУ, 2002
4. Кушнир. Ф.В. Электрорадиоизмерения М.: «Энергоатомиздат», 1983 год.
Лист замечаний