Приложение № 1
Краткий конспект
по теме «Равномерное движение тела по окружности»
Простейшим видом криволинейного поступательного движения тела является его движение по кругу, когда все точки тела движутся по одинаковым кругах. Такое движение встречается довольно редко: так двигаются кабинки смотровых колес в городских парках. В то же время любое сложное криволинейное движение тела на достаточно малом участке его траектории можно приближенно рассматривать как равномерное движение по окружности. Поэтому изучать произвольное криволинейное движение надо начинать от простого: изучение равномерного движения по окружности. Примерами равномерного движения по окружности можно приближенно считать: движение искусственных спутников Земли, движение вращающихся частей в механизмах и т.д.
Начнем изучение этого движения с важной кинематической величины мгновенной скорости. Мгновенная скорость в любой точке криволинейной траектории движения тела направлена по касательной к траектории в этой точке.
В этом можно убедиться, наблюдая за работой на точиле. Если прижать к вращающемуся точильному камню конец стальной дротини, то вы увидите, как раскаленные частицы отрываются от камня в виде искр. Эти частицы летят с той скоростью, которую они имели в момент отрывания от камня. Направление движения искр совпадает с касательной к окружности в той точке, где дротина касается камня. По касательной к окружности движутся также брызги от колес автомобиля, что пробуксовывает.
Модуль мгновенной скорости во время равномерного движения по окружности с течением времени не меняется. Равномерным движением по окружности называют движение, во время которого тело (материальная точка) за любые равные промежутки времени проходит одинаковые отрезки дуг. Примерами равномерного движения по окружности можно приближенно считать: движение искусственных спутников Земли, движение вращающихся частей в механизмах и т.д. Скорость такого движения материальной точки по линии (окружности) по модулю является постоянной и в каждой точке окружности направлена по касательной.
Положение точки A, что движется вдоль круга, определяют радиус-вектором 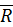 , проведенным из центра окружности O до этой точки (рис. 1). Модуль радиуса-вектора равна радиусу этого круга R.
, проведенным из центра окружности O до этой точки (рис. 1). Модуль радиуса-вектора равна радиусу этого круга R.
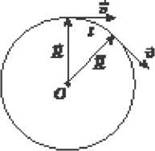
Рис. 1

Рис. 2
Скорость движения тела по окружности (линейную скорость) по аналогии с равномерным прямолинейным движением можно найти по формуле:

где l - длина дуги круга, пройденного материальной точкой за время t (рис. 2).
Пусть тело совершит один оборот по окружности, тогда формула для определения скорости примет вид:
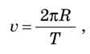
где T - это время одного оборота по окружности радиусом R. Это время называют периодом вращения. Линейную скорость измеряют в метрах в секунду (м/с).
Гораздо чаще в природе и технике встречается вращательное движение тела, когда неподвижной остается одна точка или совокупность точек, лежащих на оси вращения. Таким является движение волчка, колеса неподвижного велосипеда, стрелок часов и т.д. Во время вращения вокруг неподвижной оси O различные точки 1, 2, 3 тела (рис. 3) будут иметь разные линейные скорости 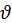 1,
1, 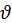 2,
2, 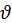 3, поэтому нельзя говорить о скорости тела. Желательно найти такие характеристики вращательного движения тела, которые были бы общими, одинаковыми для всех его точек.
3, поэтому нельзя говорить о скорости тела. Желательно найти такие характеристики вращательного движения тела, которые были бы общими, одинаковыми для всех его точек.
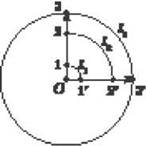
Рис. 3
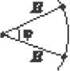
Рис. 4
Как видно из рис. 3, каждая из точек этого диска имеет свою линейную скорость, потому что за одно и то же время они проходят соответственно отрезки дуг l1 > l2 > l3. Одинаковой для этих точек будет угловая скорость вращения. Угловая скорость ω точки, равномерно движущейся по окружности, численно равна отношению угла φ, на который поворачивается радиус-вектор, до времени t и остается постоянной:
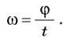
В физике углы измеряют в радианах (рад). Чтобы найти значение угла ф в радианах следует провести с его вершины произвольную дугу и найти отношение длины этой дуги к радиусу R (рис. 4):
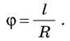
Следовательно, единицей измерения угловой скорости является 1 рад/с, что соответствует скорости точки, которая вращается равномерно и радиус-вектор которой за 1 с описывает угол в 1 рад. А формула для одного оборота по окружности примет вид:
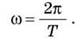
Величину, обратную к периоду вращения, называют частотой вращения и измеряют количеством оборотов за единицу времени ([ν] = 1/c):
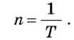
Для произвольного количества оборотов частоту вращения находят по формуле:
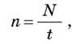
где N - число оборотов, t - время вращения тела.
После подстановки выражения для частоты вращения имеем:
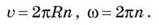
Найдем соотношение линейной и угловой скоростей на основании формулы:
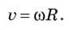
Поскольку линейная скорость изменяется по направлению, то материальная точка движется по окружности, приобретает ускорение. Ускорение тела, равномерно движущегося по окружности, в любой его точке является центростремительным, то есть напрямлене по радиусу окружности к ее центру. В любой точке вектор ускорения перпендикулярен вектору скорости. Эту особенность ускорения равномерного движения по окружности изображен на рис. 5.
Чему равен модуль центростремительного ускорения? Числовое значение (модуль) ускорение можно легко найти с рис. 5.
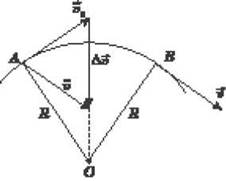
Рис. 5
Треугольник, образованный векторами 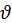 0,
0, 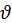 и Δ
и Δ 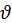 , равнобедренный, так как
, равнобедренный, так как 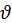 =
= 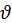 0. Треугольник OAB на рис. 5 также равнобедренный, поскольку стороны OA и OB - радиусы круга. Углы при вершинах обоих треугольников равны, потому что они образованные взаимно перпендикулярными сторонами:
0. Треугольник OAB на рис. 5 также равнобедренный, поскольку стороны OA и OB - радиусы круга. Углы при вершинах обоих треугольников равны, потому что они образованные взаимно перпендикулярными сторонами: 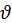 0
0 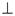 OA и
OA и 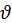
 OB. Поэтому треугольники подобны, как равнобедренные с равными углами при вершинах. Из подобия треугольников следует пропорциональность соответствующих сторон:
OB. Поэтому треугольники подобны, как равнобедренные с равными углами при вершинах. Из подобия треугольников следует пропорциональность соответствующих сторон:

где 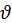 и Δ
и Δ 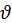 - модули скорости и изменения скорости во время перехода из точки A в точку B, R - радиус круга. Если точки A и B очень близки друг к другу, то хорду AB нельзя отличить от дуги AB. А длина дуги AB - это путь, пройденный телом с постоянной по модулю скоростью
- модули скорости и изменения скорости во время перехода из точки A в точку B, R - радиус круга. Если точки A и B очень близки друг к другу, то хорду AB нельзя отличить от дуги AB. А длина дуги AB - это путь, пройденный телом с постоянной по модулю скоростью 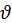 . Он равен
. Он равен 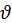 t. Поэтому можно записать:
t. Поэтому можно записать:
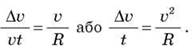
Поскольку интервал времени t, что рассматривается, очень мал, то Δ 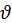 /t - это модуль ускорения. Следовательно,
/t - это модуль ускорения. Следовательно,
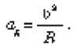
Другие выражения для центростремительного ускорения:
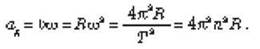
Таким образом, во время равномерного движения по окружности во всех точках круга центростремительному ускорению по модулю одинаковое. Однако направлено оно всегда по радиусу к центру (рис. 6) так, что направление ускорения от точки к точке меняется. Поэтому равномерное движение тела по окружности нельзя считать равноускоренным.
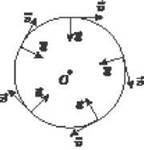
Рис. 6
Любое движение по криволинейной траектории можно представить как движение по дугам окружностей различных радиусов. Одну из сложных траекторий, по которой движется тело, и центростремительному ускорению тела в разных ее точках изображено на рис. 7:
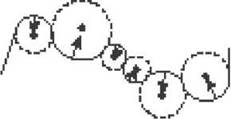
Рис. 7
Следовательно, в любой точке криволинейной траектории тело движется с ускорением, направленным в центр того круга, частью которого является участок траектории вблизи этой точки. А модуль ускорения зависит от скорости тела и от радиуса соответствующего круга.
Приложение № 2
Таблица физических величин, характеризующих равномерное движение тела по окружности.
| Название физической величины | Буквенное обозначение | Определение | Формула | Величины, входящие в формулу (с ед. измер.) |
| Период вращения | Т | Периодом называется время, в течение которого тело совершает один полный оборот | 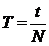
| Т – период, с t- время, с N- количество оборотов |
| Частота вращения | ||||
| Угловая скорость | ||||
| Линейная скорость | ||||
| Центростремительное ускорение | ||||
| Центростремительная сила |
Таблица № 2
| № п/п | Характеристики, связывающие величины | Формулы |
| Связь периода с линейной частотой | ||
| Связь линейной скорости с периодом и частотой | ||
| Связь линейной скорости с угловой скоростью | ||
| Связь ускорения с периодом и частотой | ||
| Связь ускорения с угловой скоростью |
Приложение № 3
Примеры решения задач
Задача 1
Трамвайный вагон движется по закруглению со скоростью 3,5 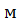 /c и центростремительным ускорением 0,5м/
/c и центростремительным ускорением 0,5м/ 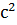 . Определить радиус закругления.
. Определить радиус закругления.
Дано:
 /c;
a /c;
a 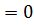 ,5м/ ,5м/ 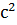
| Решение: | |
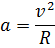
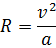
|
 Ответ: R
Ответ: R 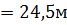
| |
| R-? |
Задача 2
Какова скорость движения автомобиля, если его колеса имеют диаметр 60см, а частота их обращения 10 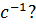
Дано:
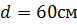 ; ;
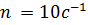 ; ;
| СИ: | Решение: | |||
| 0,6м | 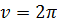 rn rn
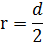
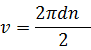

|
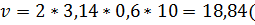 м/c);
Ответ: м/c);
Ответ: 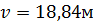 /c; /c;
| |||
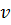 -? -?
| |||||
Задача 3
Ветровое колесо радиусом 1,2 м имеет период обращения 1,5 с. Определить центростремительное ускорение и частоту обращения концов лопастей ветрового колеса.
Дано:
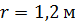 ;
T ;
T 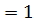 ,5 с; ,5 с;
| Решение: | |

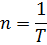
| 
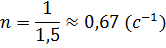 Ответ: a
Ответ: a  ;
n ;
n 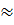 0,67 0,67 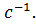
| |
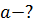

|