Теоретическая часть
Самопроизвольный необратимый процесс передачи теплоты в пространстве с неоднородным распределением температуры называется теплообменом. Теория теплообмена или теплопередача – это наука, изучающая процессы и законы передачи теплоты. Перенос теплоты представляет собой процесс обмена внутренней энергией между рассматриваемыми элементами и системами тел. Теплообмен между телами возможен лишь при наличии разности температур между ними.
Передача теплоты осуществляется различными способами. Различают три основных формы: теплопроводность, конвективный теплообмен и лучистый теплообмен.
Теплопроводность – процесс передачи теплоты при непосредственном соприкосновении различных тел или отдельных частиц тела, имеющих разные температуры.
Конвекция – процесс передачи теплоты при перемещении объемов жидкости или газа в пространстве из области с одной температурой в область с другой. При этом перенос энергии неразрывно связан с перемещением самой среды.
Тепловое излучение – это процесс передачи энергии путем электромагнитных волн. Теплообмен излучением представляет процесс последовательного превращения внутренней энергии одного тела в энергию излучения, распространения ее в пространстве и превращения энергии излучения во внутреннюю энергию другого тела.
В природе и технике элементарные процессы передачи теплоты – теплопроводность, конвекция и тепловое излучение – очень часто происходят совместно.
Теплопроводность
Теплопроводность представляет собой процесс передачи теплоты соприкасающимися, беспорядочно движущимися структурными частицами вещества (молекулами, атомами, электронами). Структурные частицы более нагретой части тела, обладающей большей энергией, соприкасаясь с окружающими частицами, передают им часть своей энергии. Как правило, теплопроводность в чистом виде возможна только в сплошных по структуре твердых телах.
Этот вид теплообмена наблюдается в любых термически неравновесных телах или системах тел. Механизм переноса энергии зависит от физического состояния тел.
В металлах перенос теплоты осуществляется путем движения (диффузии) свободных электронов; передача теплоты за счет упругих колебаний кристаллической решетки второстепенна.
В жидкостях, в твердых телах – диэлектриках перенос теплоты осуществляется путем непосредственной передачи теплового движения молекул и атомов соседним частицам вещества.
В газах перенос теплоты теплопроводностью происходит вследствие обмена энергией при соударении молекул, имеющих различную скорость теплового движения (путем диффузии молекул и атомов).
Закон Фурье
Изучая явление теплопроводности, Фурье (1822 г.) установил, что количество передаваемой теплоты (Q t) пропорционально градиенту температуры, времени и площади сечения, перпендикулярного направлению распространения теплоты. Эта гипотеза экспериментально подтверждена. Математическое выражение для определения теплового потока, переданного теплопроводностью, называется основным законом теплопроводности – законом Фурье:
Q = - l ×grad t × F, (1)
где Q =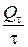 
– тепловой поток, Вт; t – время, с; l – коэффициент теплопроводности, Вт/(м.К); grad t – градиент температуры, К/м (оС/м); t (T) – температура, oС (К); F – площадь поверхности теплообмена, м2.
Для плотности теплового потока (q =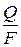 
) закон Фурье имеет вид:
q = - l ×grad t. (2)
Знак “ - ” показывает, что вектора теплового потока (плотности теплового потока) и градиента температуры направлены в противоположные стороны. В отличии от вектора теплового потока, вектор градиента температуры направлен в сторону увеличения температуры.
Физический смысл коэффициента теплопроводности l – количество теплоты, переданное в единицу времени через единицу площади изотермической поверхности при единичном значении температурного градиента. Численное значение l характеризует способность вещества передавать теплоту.
Значения коэффициента теплопроводности веществ находятся в пределах l » 0,006 ¸ 420 Вт/(м.К).
Коэффициент теплопроводности однородных твердых тел зависит только от температуры, для жидкостей и тем более газов на значения l влияет давление. Для пористых твердых тел (тепловая изоляция, строительные материалы, горные породы и т.д.) на величину коэффициента теплопроводности дополнительно влияет объем порового пространства и степень заполнения его жидкостью или газом.
Лучшими проводниками теплоты являются металлы, у которых коэффициент теплопроводности l » 10 ¸ 420 Вт/(м.К). Меньшие значения l характерны для жаропрочных сплавов, наибольшие значения коэффициента теплопроводности характерны для чистых и особенно благородных металлов. Как правило, с увеличением температуры для чистых металлов наблюдается уменьшение численного значения l, а для сплавов – увеличение l.
Значения коэффициента теплопроводности жидкостей изменяются в пределах l » 0,07 ¸ 0,7 Вт/(м.К). Для большинства жидкостей, кроме воды и глицерина, наблюдается уменьшение численных значений коэффициента теплопроводности с ростом температуры.
Хуже всего теплоту теплопроводностью передают газы. Коэффициент теплопроводности для них возрастает с увеличением температуры и изменяется в пределах l » 0,006 ¸ 0,1 Вт/(м.К).
При проведении теплотехнических расчетов используются значения коэффициентов теплопроводности из справочников. Значения l некоторых материалов представлены в табл. 1.
Таблица 1
Значения коэффициентов теплопроводности некоторых материалов
при нормальных условиях
| №№ пп | Материал | l, Вт/(м.К) |
| Алюминий | ||
| Медь | ||
| Латунь | ||
| Сталь углеродистая 30 | ||
| Сталь 1Х13 | ||
| Сталь 0Х18Н12Б | ||
| Чугун серый | ||
| Асбестовое волокно | 0,88 | |
| Бетон | 1,28 | |
| Минеральная вата | 0,05 | |
| Пенобетон | 0,11 | |
| Шлаковая вата | 0,06 |
Пределы изменения значений коэффициентов теплопроводности веществ, используемых в нефтегазовом деле приведены в табл. 2.
Таблица 2
Значения коэффициентов теплопроводности некоторых веществ
| №№ пп | Вещество | l, Вт/(м.К) |
| Глинистый буровой раствор | 0,6¸1 | |
| Горная порода | 0,22¸6,5 | |
| Нефть и нефтепродукты | 0,09¸0,14 | |
| Пластовая вода | 0,45¸0,68 | |
| Природный газ | 0,01¸0,10 |
Материалы, имеющие значение коэффициента теплопроводности при нормальных условиях l £ 0,25 Вт/(м.К) называются теплоизоляционными. Так как теплоизоляционные материалы являются пористыми телами, а поры заполнены газами (воздухом), то чем больше пористость, тем меньше значение коэффициента теплопроводности. Если поровое пространство вместо газа будет заполнено жидкостью, то значение коэффициента теплопроводности материала существенно увеличится.
Для теплоизоляционных материалов с увеличением температуры возрастают численные значения коэффициента теплопроводности.
Температурная зависимость значений коэффициента теплопроводности веществ и материалов для определенного температурного интервала обычно принимается линейной:
l = lo(1 + b×t), (3)
где lo – коэффициент теплопроводности при температуре 0°C; b – постоянная, характеризующая увеличение (уменьшение) l материала при повышении его температуры на 1°C (1 К).
Знание численных значений коэффициентов теплопроводности веществ и материалов необходимо специалисту нефтянику, газовику и нефтехимику для правильного проведения теплотехнических расчетов на различных стадиях технологического процесса в нефтегазовом деле.
Теплопроводность через плоские однослойные стенки
Любая практическая задача теплообмена в итоге сводится к вычислению теплового потока или определения температурного поля.
Температурное поле – совокупность значений температур во всех точках тела на выбранный момент времени:
t = t(x, y, z, t ), (4)
где x, y, z – координаты.
Стационарное температурное поле характеризуется постоянством температуры в каждой точке тела. Если температура изменяется только по одной координате (х) и не зависит от времени, тогда стационарное температурное поле для однослойной стенки запишется в виде:
t = t(x). (5)
Для определения температурного поля в плоской однослойной стенке используется дифференциальное уравнение теплопроводности без внутренних источников теплоты:
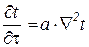, (6)
где а =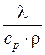 
– коэффициент температуропроводности, м2/с; ср – удельная массовая изобарная теплоемкость, Дж/(кг.К); r – плотность, кг/м3; 
=
= 
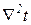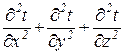– оператор Лапласа.
Согласно формулам (5) и (6) дифференциальное уравнение стационарной теплопроводности через плоскую однослойную стенку имеет вид:
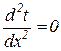. (7)
При последовательном интегрировании уравнения (7) получается:
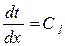, t = C1×x + C2, (8)
где C1 и C2 – константы интегрирования, которые определяются с учетом граничных условий III - его рода (постоянство температуры на внешних границах тела).
В результате получается уравнение стационарного одномерного температурного поля (рис. 1):
t = tc1 - (tc1 - tc2)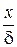 
, (9)
|
 |
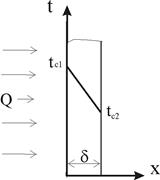Согласно формуле (9) температурное поле в плоской однослойной стенке представляет собой уравнение прямой линии.
Тепловой поток, передаваемый теплопроводностью через плоскую однослойную стенку, определяется по закону Фурье (1) с учетом выражений температурного поля (8) и (9):
Q =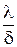 
(tc1 - tc2) × F. (10)
Плотность теплового потока через стенку:
q = 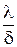(tc1 - tc2). (11)
Так как температуры поверхностей плоской стенки постоянны во времени, площадь поверхности плоской стенки одинакова с обеих сторон, то значения теплового потока Q и плотности теплового потока q не меняются во времени и по толщине стенки.
Формулы для определения теплового потока (10) и плотности теплового потока (11) можно привести к виду:
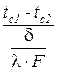Q = 
, q =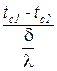 
, (12)
где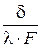 
, 
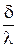– полное и удельное термическое сопротивление передачи теплоты теплопроводностью.
Из соотношения (12) видно, что при стационарной теплопроводности перепад температур на плоской стенке прямо пропорционален термическому сопротивлению и обратно пропорционален величине коэффициента теплопроводности.