Лекция 1.5. Прямая на плоскости
Уравнение линии на плоскости
Уравнением линии на плоскости называется уравнение относительно переменных x,y, которому удовлетворяют координаты каждой точки этой линии и только они.
Общий вид уравнения линии в декартовой системе координат: 
.
Это уравнение определяет линию как некоторое геометрическое место точек, т.е. совокупность точек, обладающих некоторым свойством, исключительно им присущим.
Чтобы составить уравнение линии как некоторого геометрического места точек, необходимо:
a) взять на линии произвольную точку с текущими координатами x и у;
b) записать общее свойство точек данного геометрического места в виде тождества;
c) преобразовать полученное тождество в уравнение.
Точки пересечения двух линий 
и 
находят из системы уравнений 
. Если система совместна, то линии пересекаются. Число точек пересечения равно числу решений системы.
- Прямая на плоскости
Пусть на плоскости зафиксирована точка М0, принадлежащая прямой L, положение которой в заданной системе координат xOy определяет вектор 
. Ненулевой вектор 
. Вектор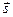 
в дльнейшем будем называть направляющим вектором прямой L.
Теорема 2.1. Множество радиусов-векторов точек прямой L представимо в виде 
, где 
- произвольный вещественный параметр.
 |
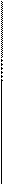М0
М
L.
 |
|
|
О
Доказательство.
Пусть некоторая точка М, положение которой на плоскости определяет вектор 
, принадлежит прямой L. Ненулевой вектор 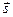образует базис на прямой L. Поэтому любой, лежащий на этой прямой вектор 
может быть для каждого представлен единственным образом в виде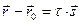 
. Тогда 
.
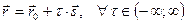Теорема доказана.
Теорема 2.2. Всякая прямая в декартовой системе координат может быть задана уравнением вида 
, где 
Доказательство.
Условие коллинеарности векторов и 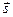в координатной форме имеет вид:
.
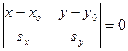Следовательно, 
Введем обозначения: 
, 
, 
. Тогда .
Таким образом, уравнение прямой на плоскости в декартовой системе координат есть уравнение первой степени относительно текущих координат x,y. Отметим, что условие вытекает из того, что 
.
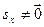Теорема доказана.
Теорема 2.3. Всякое уравнение вида
, где
в любой декартовой системе координат есть уравнение некоторой прямой.
Общее уравнение прямой называется полным, если все его коэффициенты A, B и C отличны от нуля.
Если хотя бы один из коэффициентов равен нуля, то уравнение называется неполным.
8 С=0, 
, 
, 
, 
, 
;
8 B=0, , 
, 
, 
, 
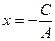- прямая параллельна оси Оу;
8 А=0, , , 
, 
, 
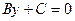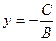- прямая параллельна оси Ох;
8 B=С=0, , 
, 
- ось Оу;
8 А=С=0, , 
, 
- ось Ох.
Способы задания прямой на плоскости
Ø 
Уравнение прямой в отрезках
Пусть прямая L задана полным общим уравнением . При построении прямой воспользуемся тем, что одну из координат точки прямой можно выбрать произвольно .
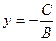При , . При ,
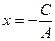
Обе эти точки лежат на осях и поэтому величины 
, 
называются отрезками, осекаемыми на осях, и в нашем случае могут быть приняты в качестве параметров прямой
, 
, 
.
Ø Уравнение прямой, проходящей через две несовпадающие точки
Пусть точки 
и 
Векторы 
и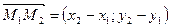 
коллинеарны, следовательно, их координаты пропорциональны
, 
- угловой коэффициент прямой L.
Ø Уравнение прямой, заданной точкой и нормальным вектором.
Пусть 
, 
, 
, 
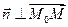Ø 
Каноническое уравнение прямой (уравнение прямой, проходящей через заданную точку, параллельно направляющему вектору)
Дано: , 
, - направляющий вектор прямой 
L.
, 
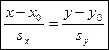
Ø Параметрическое уравнение прямой
Параметрическое уравнение прямой элементарно получается из канонического уравнения этой прямой. Примем за параметр t величины, стоящие в левой и правой частях 
, где 
ℝ
Ø Нормальное уравнение прямой
Рассмотрим некоторую прямую L.
Проведём через начало координат прямую, перпендикулярную к L и обозначим через Р точку пересечения этих прямых. На прямой ОР возьмем единичный вектор 
.
Поставим перед собой цель: выразить уравнение прямой L через два параметра
1) длину p отрезка ОР;
2) угол 
между и осью Ох.
Так как - единичный вектор, то 
.
точка М(х, у) 
, тогда и только тогда, когда 
, 
, т.к. 
, то 
.
Имея в виду, что 
, а , получим 
.
- нормальное (нормированное) уравнение прямой, где
р – длина перпендикуляра, опущенного из начала координат на прямую;
- угол, который этот перпендикуляр образует с положительным направлением оси Ох.
Алгоритм приведения общего уравнения прямой к нормальному виду:
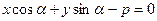
Т.к. данные уравнения определяют одну и ту же прямую, то существует такое число 
, при котором 
; 
; 
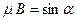. Первые два тождества возведём в квадрат и просуммируем: + 
, 
, 
- 
.
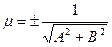Остаётся уточнить, какой из знаков 
следует взять в данной формуле. Так как расстояние 
всегда неотрицательно, то из третьего тождества заключаем, что знак нормирующего множителя противоположен знаку С.
Итак, для приведения общего уравнения прямой к нормальному виду следует умножить его на нормирующий множитель, знак которого противоположен знаку свободного члена С.
Введём теперь фундаментальное понятие – отклонение произвольной точки М от данной прямой L.
Пусто число d – это расстояние от точки М до прямой L.
Назовём отклонением 
точки М от прямой L число +d в случае, если т.М и начало координат т. О лежат по разные стороны от прямой L и число -d в случае, если т.М и начало координат т. О лежат по одну сторону от прямой L.
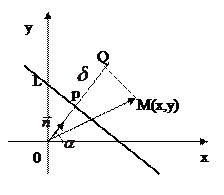Найдем ортогональную проекцию вектора 
на направление вектора
PQ = = OQ – p,
,
.
Пример. Дано общее уравнение прямой 12х – 5у – 65 = 0. Представить уравнение этой прямой в отрезках, в виде уравнения прямой с угловым коэффициентом и в виде нормального уравнения прямой.
уравнение этой прямой в отрезках: 
уравнение этой прямой с угловым коэффициентом:
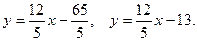
нормальное уравнение прямой:
; cosj = 12/13; sinj = -5/13; p = 5.
Cследует отметить, что не каждую прямую можно представить уравнением в отрезках. Например, прямые, параллельные осям координат или проходящие через начало координат.