Знакопеременные ряды.

– сходится.
Свойства абсолютно сходящихся рядов
1  . Если ряд абсолютно сходится, то он сходится.
. Если ряд абсолютно сходится, то он сходится.
 Т.к. ряд абсолютно сходится, т.е сходится ряд (2) то для него выполняется критерий Коши, т.е.
Т.к. ряд абсолютно сходится, т.е сходится ряд (2) то для него выполняется критерий Коши, т.е. 
 > 0
> 0  Nϵ N:
Nϵ N:  n > N p ϵ N Σ
n > N p ϵ N Σ  + …
+ … 
 . Но т.к
. Но т.к 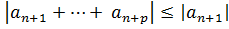 + …
+ …  , то и для ряда (1) выполняется критерий Коши.
, то и для ряда (1) выполняется критерий Коши.
2  . Если ряд (1) абсолютно сходится, а последовательность
. Если ряд (1) абсолютно сходится, а последовательность  –
–

 Т.к
Т.к  + …
+ … 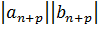




 Т.к
Т.к  - абсолютно сходится, то
- абсолютно сходится, то  > 0
> 0  ϵ N
ϵ N  + …
+ … 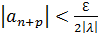 ,
,  > 0
> 0  N2 ϵ N
N2 ϵ N  p ϵ N
p ϵ N  + …
+ …  . Тогда
. Тогда 
 p ϵ N
p ϵ N  <
<  =
= 
4  . Если ряд (1) абсолютно сходится, то и ряд
. Если ряд (1) абсолютно сходится, то и ряд  , полученный перестановкой члена ряда (1), абсолютно сходится, причем сумма
, полученный перестановкой члена ряда (1), абсолютно сходится, причем сумма  ряда
ряда  равна сумме S ряда (1).
равна сумме S ряда (1).
 Докажем, что ряд
Докажем, что ряд  – сходится. Ряд
– сходится. Ряд  отличается от (1) только порядком расположения членов. Поэтому
отличается от (1) только порядком расположения членов. Поэтому  ϵ N
ϵ N  Kj ϵ N:
Kj ϵ N:  . Обозначим
. Обозначим 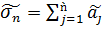
 =
=  , тогда n<
, тогда n< 
 n ϵ N и выполняется неравенство
n ϵ N и выполняется неравенство  , где
, где  – сумма ряда (2). Тогда частичные суммы
– сумма ряда (2). Тогда частичные суммы  ряда
ряда  образуют возрастающую последовательность, ограниченную сверху, т.е она сходится, значит ряд
образуют возрастающую последовательность, ограниченную сверху, т.е она сходится, значит ряд  сходится абсолютно.
сходится абсолютно.
5  . Если ряды
. Если ряды  и s w:space="720"/></w:sectPr></w:body></w:wordDocument>">
и s w:space="720"/></w:sectPr></w:body></w:wordDocument>">  абсолютно сходятся, то ряд
абсолютно сходятся, то ряд 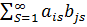 , (*) составленный из всевозможных попарных произведений членов рядов (1) и s w:space="720"/></w:sectPr></w:body></w:wordDocument>">
, (*) составленный из всевозможных попарных произведений членов рядов (1) и s w:space="720"/></w:sectPr></w:body></w:wordDocument>">  , абсолютно сходится, причем сумма ряда (*) равна произведению сумм рядов
, абсолютно сходится, причем сумма ряда (*) равна произведению сумм рядов  и s w:space="720"/></w:sectPr></w:body></w:wordDocument>">
и s w:space="720"/></w:sectPr></w:body></w:wordDocument>">  .
.
 Докажем, что ряд
Докажем, что ряд  Рассмотрим его частичную сумму
Рассмотрим его частичную сумму 
 , где
, где  – суммы рядов
– суммы рядов  и
и  . Т.е. частичные суммы ряда
. Т.е. частичные суммы ряда  ограничены сверху. Т.к. это ряд с неотрицательными членами, то ряд сходится.
ограничены сверху. Т.к. это ряд с неотрицательными членами, то ряд сходится.
Докажем, что  , где
, где  – суммы рядов (*), (1) и
– суммы рядов (*), (1) и  соответственно. Заметим, что все члены ряда (*) содержатся в следующей таблице:
соответственно. Заметим, что все члены ряда (*) содержатся в следующей таблице:
 1
1
| 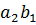 2
2
|  5
5
| … |
 4
4
| 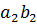 3
3
| 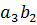 6
6
| … 11 |
 9
9
|  8
8
|  7
7
| … 12 |
| … | … 15 | … 14 | … 13 |
Пронумеруем элементы этой таблицы «методом квадратов».
Рассмотрим ряд  образованный из всевозможных произведений
образованный из всевозможных произведений 
По доказанному,  вида (*), в частности последний ряд, абсолютно сходится, а его сумма не зависит от порядка расположения его членов. Поэтому последний ряд сходится и его сумма =
вида (*), в частности последний ряд, абсолютно сходится, а его сумма не зависит от порядка расположения его членов. Поэтому последний ряд сходится и его сумма = 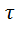
Пусть  – частичные суммы рядов (1),
– частичные суммы рядов (1),  и последнего ряда. Тогда
и последнего ряда. Тогда  . Т.к. s w:val="28"/></w:rPr><m:t>n</m:t></m:r></m:sub></m:sSub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в†’S</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
. Т.к. s w:val="28"/></w:rPr><m:t>n</m:t></m:r></m:sub></m:sSub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>в†’S</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  ,
,  при
при  , то
, то  при
при  .
.
C другой стороны, 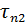 – подпоследовательность последовательности
– подпоследовательность последовательности  , поэтому,
, поэтому,  . Значит
. Значит  .
.
Знакочередующиеся ряды
 , где s w:val="28"/></w:rPr><m:t>n</m:t></m:r></m:sub></m:sSub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>>0</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
, где s w:val="28"/></w:rPr><m:t>n</m:t></m:r></m:sub></m:sSub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>>0</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
 ϵ N наз. знакочередующимся. (3)
ϵ N наз. знакочередующимся. (3)
Теорема Лейбница
Если последовательность  монотонно стремится к нулю, т.е
монотонно стремится к нулю, т.е 
 ϵ N и
ϵ N и  , то знакочередующийся ряд (3) сходится.
, то знакочередующийся ряд (3) сходится.
 Пусть
Пусть  , тогда
, тогда 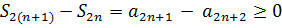 , т.е.
, т.е.  – возрастающая последовательность. Кроме того,
– возрастающая последовательность. Кроме того,  =
=  (т.к.
(т.к.  и
и 
 ϵ N), т.е.
ϵ N), т.е. 
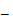 ограничена сверху. Значит
ограничена сверху. Значит 
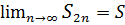 , т.е. ряд расходится.
, т.е. ряд расходится.
Следствие. Для знакочередующегося ряда (3)  ϵ N справедливы неравенства:
ϵ N справедливы неравенства:  ;
;  .
.
 Заметим, что
Заметим, что  . Т.к.
. Т.к.  , то
, то 
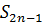 . Значит,
. Значит, 
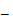 убывающая последовательность. Итак,
убывающая последовательность. Итак,  предел возрастающей последовательности
предел возрастающей последовательности  и убывающей последовательности
и убывающей последовательности  . Значит,
. Значит,  . Перепишем это в виде:
. Перепишем это в виде:
 . Отсюда
. Отсюда  ,
,  , т.е.
, т.е.  ϵ N выполняется
ϵ N выполняется 
Пример.  ,
,  сходится, т.к.
сходится, т.к. 
 монотонно убывает.
монотонно убывает.
Пример.  сходится при
сходится при  и расходится при
и расходится при  .
.
 Рассмотрим
Рассмотрим  .
. 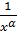 и
и  сходятся при
сходятся при  и расходятся при
и расходятся при  .
.
Признаки Абеля и Дирихле сходимости рядов.
Теорема 1. (признак Дирихле).
Ряд  (4) сходится, если:
(4) сходится, если:
1) Последовательность частичных сумм ряда  ограничена, т.е.
ограничена, т.е.  :
:  ϵ N
ϵ N 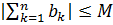
2)Последовательность  монотонна, стремится у нулю. (без доказательства).
монотонна, стремится у нулю. (без доказательства).
Теорема 2. (признак Абеля)
Ряд (4) сходится, ели ряд  сходится, а последовательность
сходится, а последовательность  монотонна и ограничена.
монотонна и ограничена.
Т.к. последовательность  монотонна и ограничена, то
монотонна и ограничена, то 
Тогда  монотонна и стремится к нулю. Т.к.
монотонна и стремится к нулю. Т.к.  сходится, то последовательность его частичных сумм ограничена. Поэтому
сходится, то последовательность его частичных сумм ограничена. Поэтому  сходится по признаку Дирихле. Т.к.
сходится по признаку Дирихле. Т.к. 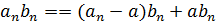 и ряд
и ряд  сходится, то
сходится, то  сходится.
сходится.
Условно сходящиеся ряды
Ряд  называется условно сходящимся, если он сходится, а ряд
называется условно сходящимся, если он сходится, а ряд  расходится.
расходится.
Пример. 
Теорема Римана. Если ряд  сходится условно, то
сходится условно, то  числа
числа  (или
(или  ) можно так представить члены этого ряда, что последовательность частичных сумм получившегося ряда будет иметь
) можно так представить члены этого ряда, что последовательность частичных сумм получившегося ряда будет иметь  своим пределом, при
своим пределом, при  . (без доказательства)
. (без доказательства)