Введение. Основная теорема векторного анализа

Теория электромагнитного поля

Спецкурс для студентов специальности «Прикладная математика», 32 часа

Литература

1. Тамм И.Е. Основы теории электричества. 2003.
2. Нейман Л.Ф., Демирчян К.С. Теоретические основы электротехники Т.2. 2003.
3. Фейнман Ф., Лейтон Ф., Сэндс М. Фейнмановские лекции по физике Т.5. Электричество и магнетизм Т.6. Электродинамика. 1977.
4. Шимони К. Теоретическая электротехника. 1964.
5. Калашников С. Г. Электричество. 1985.
6. Пановский В., Филипс М. Классическая электродинамика. 1963.
7. Татур Т. А. Основы теории электромагнитного поля. Справочное пособие. 1989.

Введение. Основная теорема векторного анализа

1. Векторные поля и их источники. Термин поле имеет разный смысл в физике и математике. Для физика поле – это вид материи, состояние которого в пространстве и времени описывается одной или несколькими физическими величинами. Для математика поле – это скалярная или векторная функция пространственных координат x,y,z и времени t, например φ (x,y,z,t) или А (x,y,z,t). Поля, которые не изменяются с течением времени, как например, φ (x,y,z) или А (x,y,z) называются постоянными или стационарными. В дальнейшем речь идет, как правило, о математических векторных полях, точнее, о непрерывных и дифференцируемых векторных функциях. Непрерывность и дифференцируемость функций могут нарушаться только в отдельных точках, на некоторых линиях или поверхностях в пространстве или в отдельные моменты времени.

Векторные поля имеют два вида источников. Из мест расположения источников первого вида расходятся силовые линии поля, или в эти места сходятся силовые линии. Например, силовые линии потока жидкости начинаются на поверхности тающей глыбы льда, а силовые линии электрического поля исходят от положительных электрических зарядов. Вокруг источников второго вида замыкаются силовые линии поля. Например, линии потока жидкости замыкаются вокруг верхушки опущенной в воду, а силовые линии магнитного поля замыкаются вокруг проводов, по которым течет электрический ток.

Источники первого вида векторного поля

A (x,y,z) = A_x(x,y,z) i + A_y(x,y,z) j + A_x(x,y,z) k

обнаруживаются с помощью операции дивергенции, которая в декартовых координатах записывается в виде

Источники второго вида обнаруживаются с помощью операции ротора

.

Если известны источники векторного поля, то решение дифференциальных уравнений с частными производными, которым это поле подчиняется, сводится к вычислению интегралов.

Если , то поле А называется потенциальным. Оно создается источниками первого вида, у него нет источников второго вида.

Если , то поле А называется соленоидальным. Оно создается источниками второго вида, но не имеет источников первого вида.

2. Основная теорема векторного анализа. Любое непрерывно дифференцируемое векторное поле A (x,y,z), заданное в неограниченном трехмерном пространстве и исчезающее на бесконечности со своими дивергенцией и ротором, может быть единственным образом (с точностью до векторной постоянной) представлено в виде суммы потенциального Р (x,y,z) и соленоидального S (x,y,z) полей, т.е.

,

где и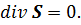

Замечания к формулировке теоремы:

1. Формулировка теоремы несколько упрощена, чтобы упростить доказательство и сосредоточить внимание на главном, на возможности разделить векторное поле на потенциальную и соленоидальную составляющие. В точках на линиях и поверхностях, где нарушается непрерывность поля А или непрерывность его производных, находятся источники поля, которые определяются не с помощью операций и , а другими способами. Влияние этих источников на поле А пришлось бы учитывать, усложняя доказательство.
2. Условие, согласно которому, поле А, его дивергенция и ротор принимают на бесконечности нулевые значения, равносильно требованию, чтобы источники поля А находились в ограниченной части пространства. Чем дальше от источников, тем слабее поле А, поэтому на бесконечности . В случае двумерных полей, когда источники находятся, например, внутри бесконечно длинного цилиндра, доказательство теоремы и формулы для составляющих поля изменяются.
3. Поле А задается однозначно, но неоднозначно (с точностью до векторной постоянной) разделяется на потенциальную Р и соленоидальную S составляющие. Другими словами, если , то возможно, что , где C – векторная постоянная. Функции и можно рассматривать как потенциальную и соленоидальную составляющие наряду с функциями Р и S.
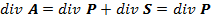4. Так как и , то источники первого вида поля А совпадают с источниками поля Р, а источники второго вида поля А такие же, как источники поля S.
5. Доказательство теоремы представляет интерес потому, что в ходе его получаются важные представления для потенциальной и соленоидальной составляющих поля А.

Доказательство

1. Построение поля Р. Это поле удовлетворяет уравнениям

,

Так как при любой скалярной функции φ, то поле Р обладает скалярным потенциалом φ, таким, что

,

где – постоянный вектор. Подставив последнее выражение для Р во второе уравнение, получаем, что

, или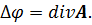

Здесь s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> – оператор Лапласа (лапласиан), примененный к функции φ. В декартовых координатах

и соответственно

В неограниченном пространстве скалярный потенциал φ определяется посредством интегрирования источников:

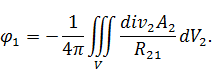
В математической физике эта формула известна как фундаментальное решение уравнения Пуассона . Интегрирование выполняется по неограниченному объему V, но на практике приходится брать интеграл по объему области, в которой отлична от нуля. В выражении для потенциала использованы следующие обозначения: индексом 1 отмечена точка поля (наблюдения), индексом 2 – точка интегрирования (источника), соответственно φ₁=φ (x₁,y₁,z₁), A₂ = A (x₂,y₂,z₂); индекс 2 при означает, что дифференцирование выполняется по координатам точки 2; интегрирование также выполняется по координатам точки 2 т.е. dV₂=dx₂dy₂dz₂; расстояние между точками 1 и 2

Эти обозначения иллюстрирует рис. 1. Здесь символом О помечено начало координат, R₁ и R₂ – радиус-векторы точек 1 и 2, вектор R₂₁ направлен из точки 2 в точку 1

Рис. 1. Два вектора расстояния между точками 1 и 2, и ;

Хотя , различие между этими величинами сказывается во многих формулах векторного анализа и математической физики,

t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/></w:rPr><m:t>.</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">

Окончательно, представляя искомое поле Р как градиент скалярного потенциала φ, получаем

2. Построение поля S. Это поле определяется системой уравнений

,

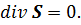
Так как при любой векторной функции f, то решение этих уравнений можно представить в виде:

Векторный потенциал f подчиним дополнительному условию . Это ограничение не является принципиально важным, его можно изменить, но в принятом здесь виде оно позволяет упростить решение. Подставим выражение для S в первое уравнение системы:

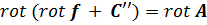, или

С учетом соленоидальности поля f по известной формуле векторного анализа находим, что

Здесь оператор Лапласа от векторной функции f представляет собой векторную сумму трех скалярных функций (лапласианов от проекций вектора f):

Соответственно уравнение представляет собой систему трех

скалярных уравнений

Объединив фундаментальные решения каждого из этих уравнений в одну векторную сумму, получаем интегральное представление векторного потенциала f в неограниченном пространстве через его источники второго вида:

Следовательно,

3. Однозначность разложения поля А. На основании формул (1) и (2) векторное поле А можно представить как сумму потенциальной и соленоидальной составляющих в следующем виде

Сумма векторных постоянных и равна нулю, так как по условию поле А исчезает на бесконечности.

Если допустить возможность другого разложения поля А на потенциальную и соленоидальную составляющие, т.е. , то разности и удовлетворяют однородным уравнениям:

и , .

В неограниченном пространстве , , где С – векторная постоянная; следовательно, .

Постоянная С сводится к нулю благодаря требованию теоремы о том, что поле , его ротор и дивергенция принимают нулевые значения на бесконечности. Таким образом, однозначность разложения доказана.

3. Следствие из теоремы. Формула (3) позволяет восстановить векторное поле А в неограниченном пространстве по его источникам (ротору и дивергенции). Для практического применения более удобно другое представление, в котором по сравнению с формулой (3) изменен порядок операций интегрирования и дифференцирования. Изменение порядка операций возможно, если несобственные интегралы в формуле (3) сходятся.

Наличие бесконечных пределов интегрирования несущественно, потому что источники поля ( или ) заданы в ограниченной части пространства и конечные размеры этой части пространства обеспечивают конечные пределы интегрирования. Наличие особой точки у подынтегральной функции требует дополнительного исследования (, когда точка поля 1 попадает в область расположения источников, которая одновременно является областью интегрирования)

Допустим сначала, что точка поля 1 находится вне области интегрирования и, следовательно, подынтегральная функция в формуле (3) непрерывна и дифференцируема; поэтому

Преобразуем подынтегральные выражения. Во – первых,

>

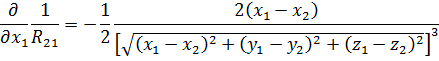
и соответственно

где – единичный вектор, указывающий направление от точки 2 к точке 1.

Заметим, что

Поэтому , а также В зависимости от того, как выбрано направление между двумя точками в пространстве, производная от расстояния между ними меняет знак.

Во – вторых, согласно формуле векторного анализа

находим

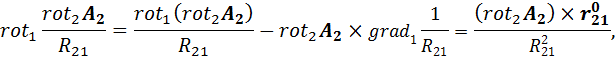
где , так как не зависит от координат точки 1.

Теперь формула (3) принимает вид

Это и есть окончательный результат, который можно рассматривать как следствие из основной теоремы векторного анализа.

Остается показать, что формула (4) справедлива, когда точка 1 попадает в область расположения источников поля А.

Разделим объем интегрирования на две части: – объем шара малого радиуса ɛ с центром в точке наблюдения 1 и – остальная часть объема . В области 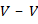подынтегральные функции в формуле (3) непрерывны и дифференцируемы, в этой области порядок интегрирования и дифференцирования не имеет значения. Перейдем к пределу при , когда шар стягивается в точку 1. Градиент объемного потенциала (первое слагаемое в формуле(3)) равен

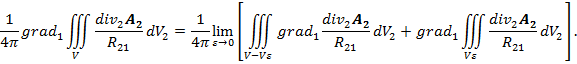
Приближенная оценка показывает, что величина объема пропорциональна а подынтегральная функция пропорциональна , значит этот интеграл в пределе стремится к нулю как . Градиент интеграла может оказаться не равным нулю, но уже можно поменять порядок дифференцирования и интегрирования. Как показано при выводе формулы (4),

Величина последнего интеграла пропорциональна ɛ, так как объем убывает как а подынтегральная функция возрастает как . Итак, интеграл по объему стремится к нулю, а

есть сходящийся несобственный интеграл, который вошел в формулу (4) в качестве первого слагаемого.

Оценка ротора объемного векторного потенциала (второго слагаемого в формуле (3)) сводится к исследованию его трех скалярных составляющих, которые аналогичны объемному скалярному потенциалу. Особенности вторых слагаемых в формулах (3) и (4) оказываются интегрируемы и обе эти формулы равносильны.

Вывод: первое слагаемое в формуле (4)

представляет собой градиент объемного потенциала и является потенциальным полем; второе слагаемое

является ротором объемного векторного потенциала и представляет собой соленоидальное поле; произвольное векторное поле допускает разложение на потенциальную и соленоидальную составляющие .

Приложение. Краткое содержание вводной лекции

Векторное поле A (x,y,z) допускает разложение на потенциальную и соленоидальную соответствующие:

, ,

Потенциальное поле Р может быть описано скалярным потенциалом, таким, что , а соленоидальное поле S – векторным потенциалом, таким, что

.

Скалярный потенциал удовлетворяет уравнению Пуассона

решение которого в неограниченном пространстве записывается в виде объемного потенциала

Векторный потенциал удовлетворяет векторному уравнению Пуассона

,

решение которого в неограниченном пространстве записывается в виде объемного векторного потенциала

Векторное поле А можно определить, интегрируя его источники: