В односкатных и двускатных балках наиболее опасное нормальное сечение (с максимальными напряжениями от изгиба) не совпадает с сечением, в котором возникает максимальный изгибающий момент, и находится на расстоянии х М от опоры с меньшей высотой (рис. 3).
а б
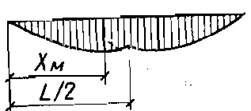
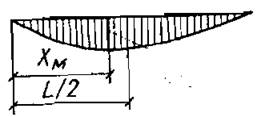
Рис. 3 Положение наиболее опасного нормального сечения в балках
в двускатной (а) и односкатной (б) при равномерно распределенной нагрузке
При равномерно распределенной нагрузке по всему пролету расстояние от опоры до этого наиболее опасного сечения находится по формулам:
А) для балок прямоугольного сечения
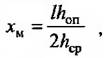
где l - расчетный пролет балки;
h оп - высота балки на опоре с меньшей высотой;
h ср - высота балки в середине пролета;
Б) для балок двутаврового и коробчатого сечения
,
здесь:
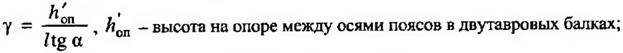
α - угол наклона верхнего пояса балки к горизонту.
Нормальное напряжение в расчетном сечении балки определяют по формуле:
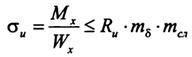
где Rи = R и А m дл.
В односкатных и двускатных балках переменного сечения следует учитывать влияние ската на напряжения изгиба параллельно поверхности. В том случае, когда волокна древесины параллельны одной из поверхностей балки и угол ската 10° (рис. 4), напряжения изгиба в крайних волокнах, параллельных поверхности, следует рассчитывать по формуле
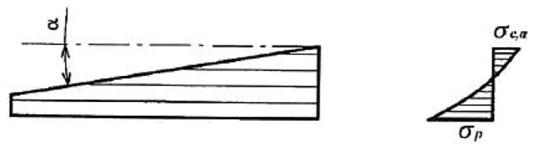
Рис. 4 Напряжения в односкатной балке
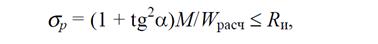
а на скатной поверхности – по формуле
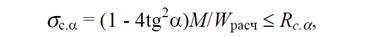
где R c,α - расчетное сопротивление древесины сжатию под углом α к направлению волокон, определяемое по формуле
Двускатные гнутоклееные балки рекомендуются к применению при уклонах не более 20%.
Криволинейные (гнутые) участки (рис. 5) клееных деревянных конструкций, изгибаемые моментом М, уменьшающим их кривизну, следует рассчитывать по формулам кривых брусьев:
|
|
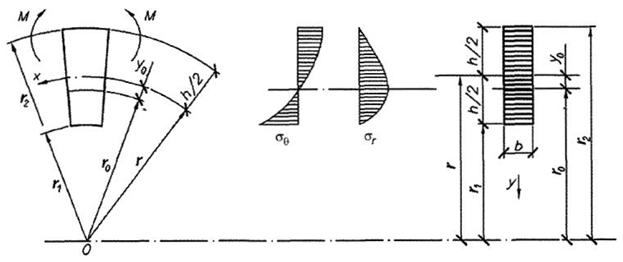
Рис. 5 - Расчетная схема кривого бруса при чистом изгибе
а) по тангенциальным нормальным напряжениям на внутренней и внешней кромках бруса:
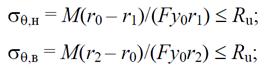
где σθ,н и σθ,в соответственно тангенциальные нормальные напряжения на внутренней и внешней кромках бруса (индексы «н» и «в» означают по рисунку «нижняя» и «верхняя» кромки);
М - расчетный изгибающий момент;
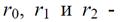соответственно радиусы кривизны нейтрального слоя, нижней (ближней к центру кривизны) и верхней кромок бруса;
F – площадь поперечного сечения кривого бруса;
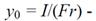смещение нейтрального слоя от геометрической оси криволинейного участка;
I – момент инерции поперечного сечения кривого бруса;
R u - расчетное сопротивление древесины изгибу;
Б) по максимальным радиальным нормальным напряжениям
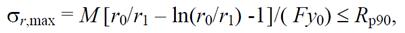
где R p90 - расчетное сопротивление клееной древесины растяжению поперек волокон.
При невыполнении этого условия по формуле допускается выполнять усиление постановкой вклеенных или ввинченных стержней, рассчитанных на восприятие растягивающего усилия, определяемого по формуле
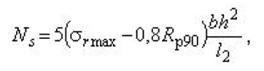
где l 2 - длина хорды криволинейного участка, на котором не выполняется условие прочности.
2 Устойчивость плоской формы деформирования балок проверяют по формуле:
,
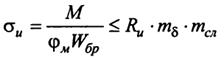где
.
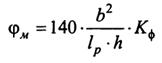где φ – коэффициент продольного изгиба сжатого пояса из плоскости изгиба балки.
Расчет на скалывание
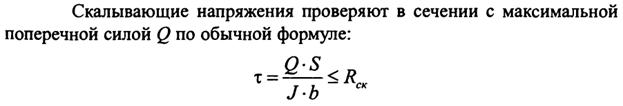
Для балок прямоугольного сечения это условие упрощается до вида
τ = 1,5 Q /(bh оп).
Проверка жесткости
f 0 – прогиб фиктивной балки постоянного сечения с наибольшими размерами рассчитываемой;
|
|
к - коэффициент, учитывающий влияние переменности высоты сечения, принимаемый за единицу для балок постоянного сечения;
с - коэффициент, учитывающий влияние деформаций сдвига от поперечной силы.
Значения коэффициентов к и с для основных расчетных схем балок приведены в таблице Е.4 приложения «Е» к СП 64.13330.2017.
В практических расчетах при проектировании балок переменного сечения удобно действовать в такой последовательности:
1 – после определения нагрузки на балку определить наибольшую поперечную силу в ней – опорную реакцию Q = ql /2;
2 – вычислить минимально допустимую высоту прямоугольного поперечного сечения балки на опоре из условия скалывания по клеевому шву, задавшись предварительно шириной поперечного сечения b и расчетным сопротивлением клееной древесины скалыванию R ск= R скА m дл П m i
h оп ≥ 1,5 Q/b R ск
3 – вычислить максимальную высоту сечения балки с учетом уклона ее верхней грани i и фактической длины L для двускатной
h max = h оп + i L /2
или h max = h оп + i L для односкатной;
4 – найти положение наиболее напряженного нормального сечения
x M = l h оп/2 h max;
5 – вычислить высоту этого сечения h = h оп + i x M и его момент сопротивления W = bh 2/6;
6 – вычислить изгибающий момент в этом сечении
M x = (q x M /2)(l - x M)
7 – произвести проверку прочности этого наиболее опасного нормального сечения
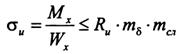
где Rи = Rи А m дл П m i.
Если это условие прочности не выполняется, необходимо увеличить на одинаковый размер высоту опорного и наибольшего сечений, добавив в зависимости от уклона ориентировочно 3-5 толщин слоев (ламелей) и произвести вторую итерацию, начиная с п. 4.
|
|
8 – рассчитать максимально допустимую длину участка между точками раскрепления сжатой кромки балки из условия φM ≥ 1, что дает формулу
l p ≤ b 2/ hm б
и учесть этот результат при конструировании связевой системы в покрытии (шаг узлов скатной связевой фермы);
9 – проверить жесткость балки с окончательно принятыми ее размерами.