Антенны в виде открытого конца волновода

Лекция 7 – 8.

Апертурные антенны

Учебные вопросы:

Рупорные антенны.

Зеркальные параболические антенны.

Двухзеркальные антенны.

Облучатели зеркальных антенн.

Антенна параболический цилиндр и уголковая антенна.

Рупорные антенны

 

Антенны в виде открытого конца волновода

В качестве слабонаправленных антенн УКВ широко используются антенны в виде открытого конца волноводов прямоугольного или круглого сечений. Электромагнитная волна, распространяющаяся по волноводу, дойдя до его открытого конца, частично излучается, а частично отражается (рис. 1, а). Физическими источниками излучения являются электрические токи, возбуждаемые главным образом на внутренних стенках волновода. Расчет излучения методом, использующим распределение тока вблизи раскрыва волновода, очень сложен, поэтому используется метод, основанный на применении принципа эквивалентности. Для этого волновод окружают замкнутой поверхностью. Эта поверхность проводится так, чтобы она совпадала с поверхностью открытого конца волновода и далее стелилась по наружным поверхностям стенок волновода. Тангенциальные составляющие поля на наружных поверхностях стенок волновода (поверхностные токи) принимаются равными нулю.

Рисунок 1. Распространение электромагнитной волны по волноводу

 

В инженерном решении приближенно полагают, что структура электромагнитного поля в плоскости открытого конца волновода такая же, как в поперечном сечении бесконечно длинного волновода, т.е. пренебрегают волнами высших типов, излучением токов, затекающих на наружные поверхности стенок волноводов, и не учитывают волны, отраженные от открытого конца волновода. В случае волновода прямоугольного сечения, возбуждаемого основной волной Н₁₀ на открытом конце существуют взаимно перпендикулярные тангенциальные составляющие поля 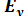и зависимость которых от координат известна (рис. 1, б).

Таким образом, характеристику направленности открытого конца волновода прямоугольного сечения в плоскости Е, параллельной размеру b поперечного сечения, можно представить в виде произведения множителя системы плоского раскрыва на характеристику направленности элемента Гюйгенса в этой плоскости. 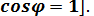В плоскости H характеристика направленности открытого конца волновода прямоугольного сечения представляет собой произведение множителя системы синфазного раскрыва с косинусоидальным распределением амплитуды возбуждающего поля на характеристику направленности элемента Гюйгенса в плоскости Н, в которой следует принять и, следовательно, Поскольку поперечные размеры прямоугольного волновода а и b невелики и соизмеримы с длиной волны (обычно для стандартных волноводов 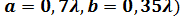то ДН антенны в виде открытого конца волновода имеет один широкий лепесток, т.е. антенна является слабонаправленной.

Следует отметить, что точность расчетов по вышеприведенным так называемым апертурным формулам является удовлетворительной только в переднем полупространстве. В задних квадрантах результаты расчета по этим формулам не обеспечивают удовлетворительного совпадения с экспериментальными данными. Это объясняется тем, что излучение в задних квадрантах как в плоскости Е,так и в плоскости H в основном определяется дифракцией на широких стенках волновода.

Характеристики направленности открытого конца волновода круглого сечения радиусом а в плоскостях Е и H можно рассчитать по приближенным формулам, полученным при тех же допущениях, что и для прямоугольного волновода. При этом множитель системы выражается цилиндрическими функциями.

Антенны в виде открытого конца волновода применяются в сантиметровом диапазоне волн в тех случаях, когда требуется широкая ДН. Их часто используют в качестве облучателей зеркальных антенн. Антенна в виде открытого конца волновода оказывается плохо согласованной со свободным пространством из-за резкого изменения условий распространения при переходе от волновода к свободному пространству. Коэффициент отражения от открытого конца прямоугольного волновода достигает значения 0,25...0,3, коэффициент отражения от открытого конца круглого волновода несколько меньше и составляет 0,1...0,25. Применяя подстроечные элементы, можно значительно снизить коэффициент отражения от открытого конца волновода.

 

1.2. Принцип действия, основные свойства рупорных антенн

Концентрация излучения в пределах более узкого телесного угла достигается увеличением размеров синфазно возбужденной поверхности. Если размеры сечения волновода выбираются таким образом, чтобы обеспечить формирование необходимой структуры поля, то, плавно увеличивая сечение волновода, эту структуру можно сохранить, а размеры излучаемой поверхности увеличить (рис. 2). В месте перехода от волновода к рупору (сечение ) возникают высшие типы волн, но при достаточно плавном расширении волновода (малый угол раствора рупора) интенсивность этих волн невелика.

Рисунок 2. Общий вид рупорных антенн

 

Существуют различные типы рупоров. Рупор, образованный увеличением размера b волновода, параллельного вектору , называется cекториальным Е- плоскостным (см рис. 2, а).Рупор, образованный увеличением размера а волновода, параллельного вектору , называется cекториальным H- плоскостным (см рис. 2, б). Рупор, образованный одновременным увеличением размеров а и b поперечного сечения волновода, называется пирамидальным (см рис. 2, в, г), а увеличением поперечного сечения круглого волновода – коническим (см рис. 2, е). При плавном переходе от волновода к рупору структура поля в последнем напоминает структуру поля в волноводе.

Векторы электромагнитного поля при переходе из волновода в рупор несколько изменяют свою форму, чтобы обеспечить выполнение граничных условий на стенках рупора (рис. 3).

Рис. 3. Векторы электромагнитного поля при переходе из волновода в рупор

Направленные свойства рупорной антенны приближенно можно анализировать, как и в случае открытого конца волновода, пользуясь принципом эквивалентности. На излучающей поверхности рупора действуют две взаимно перпендикулярные тангенциальные составляющие поля (прямоугольный раскрыв), амплитуды которых не зависят от координаты у, а вдоль координаты х они изменяются по закону косинуса.

Однако в отличие от поверхности открытого конца волновода плоская излучающая поверхность рупора не может быть синфазной, так как в раскрыве рупора имеются фазовые искажения. Найдем фазу возбуждающего поля в произвольной точке М излучающего раскрыва H-плоскостного рупора (рис. 4). Дуга NОР окружности с центром в точке 0₁ есть линия равных фаз.

Рисунок 4. Излучающий раскрыв H-плоскостного рупора

 

Предполагая для простоты, что в рупоре получаем

где - длина H-плоскостного рупора. Обычно 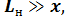поэтому можно ограничиться первым членом разложения. Тогда . Следовательно, в раскрыве рупорной антенны имеется примерно квадратичное фазовое распределение. Максимальный сдвиг фаз на краях раскрыва , тогда

(1)

При достаточно больших значениях ДН рупорной антенны заметно отличается от ДН синфазной излучающей поверхности. При этом симметрия ДН относительно нормали к возбужденной поверхности сохраняется.

Максимальный сдвиг фаз на краю раскрыва конического рупора (радиус раскрыва , длина рупора L)

(2)

Поскольку в рупорной антенне практически невозможно добиться полной синфазности излучающей поверхности, то обычно, задаваясь некоторым допустимым сдвигом фаз, выбирают размеры раскрыва рупора и его длину. Этот сдвиг должен быть таким, чтобы ДН рупорной антенны мало отличалась от ДН синфазной излучающей поверхности, размеры которой равны размерам раскрыва рупора.

Допустимый максимальный сдвиг фаз определяется условием получения максимального КНД при заданной относительной длине рупора. С увеличением относительных размеров раскрыва рупора 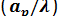или при неизменной длине его ДН сначала становится уже и КНД растет, так как увеличиваются размеры излучающей поверхности, которая практически остается синфазной. При дальнейшем увеличении размеров заметно растут фазовые искажения, вследствие чего ДН начинает расширяться и КНД уменьшается. На рис.5 по оси ординат отложено произведение КНД E–плоскостного рупора на отношение .

 

Рисунок 5. Зависимость произведения КНД E–плоскостного рупора на отношение

 

Аналогичные кривые существуют и для H-плоскостных рупоров. При заданном отношении имеется определенное оптимальное значение или 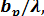при котором КНД антенны - максимально возможный. Оптимальному значению или 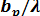соответствует допустимый сдвиг фаз. Рупор, размеры которого подобраны так, чтобы при заданной длине получить максимальный КНД, называется оптимальным.

Из (1) видно, что для того, чтобы при увеличении размеров раскрыва рупора максимальный сдвиг фаз не изменялся, оставаясь равным допустимому, т.е. КНД возрастал, относительная длина рупора должна увеличиваться пропорционально квадрату относительных размеров раскрыва рупора. Анализ кривых, приведенных на рис.5, показывает, что в случае E-плоскостного рупора максимальный КНД получается при выполнении равенства

. (3)

Увеличение допустимого сдвига фаз в случае H-плоскостного рупора по сравнению с E-плоскостным объясняется спаданием амплитуды возбуждающего поля к краям этого рупора в плоскости H. Коэффициент направленного действия оптимального E- или H-плоскостного рупора с учетом несинфазности и неравномерности возбуждения составляет 0,64.

В настоящее время находят применение рупоры, у которых сдвиги фаз поля в раскрыве значительно превосходят максимально допустимые. При больших по сравнению с λ раскрывах и и больших углах растворов рупора 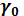ДН становится по форме близкой к столообразной. Такие расфазированные рупоры обладают более широким рабочим диапазоном, чем синфазные рупоры. Их ДН при сравнительно мало зависят от частоты.