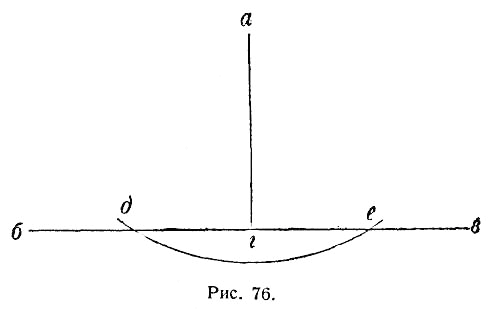
Модульная сетка
Модульная сетка позволяет добиться пропорциональности элементов дизайна участка между собой, по отношению к дому и участку в целом, так как она основана на архитектурных размерах здания, в конкретном случае - жилого дома. Таким образом, жилой дом служит отправной точкой проектирования, и заложенные в нем архитектурные пропорции переносятся на прилегающие к нему ландшафтные объекты, т.е. модульная сетка как бы продолжает проектировочное решение жилого пространства дома и служит связующим звеном между ним и садом.
Как определить размер модульной сетки?
1. Определить расстояние между центрами оконных простенков. Если этот размер повторяется хотя бы дважды, этого достаточно для построения модульной сетки.
2. Бывает, что модульная сетка "обнаруживается" в размерах эркеров, башенок, выступах зданий.
3. Как правило, архитектурные параметры жилых пространств непосредственно связаны с размерами человеческой фигуры. Наиболее часто встречающие размеры модульной сетки варьируются в пределах 2,5-4м. Эти размеры, с некоторыми оговорками, уместны и в ландшафтном проектировании.
Итак, определив размеры модуля сетки, начинают её вычерчивание. Для этого удобно сделать ксерокопию масштабного плана участка или наложить на масштабный план лист кальки, закрепив его по углам.
Удобно начинать вычерчивание сетки от фасада дома, причем линии сетки должны быть строго перпендикулярны дому и распространяться до границ участка. Не страшно, если забор или дополнительные постройки на участке располагаются под углом к дому и, как следствие, к линии сетки на масштабном плане.
По готовой модульной сетки можно продолжить процесс проектирования. Для этого необходимо сделать несколько копий масштабного плана участка с модульной сеткой (или масштабного плана с закрепленным поверх него листом кальки с сеткой). Теперь можно выполнить три (а возможно, и больше) варианта предварительного рисунка дизайна участка.
Для этого нужно обратиться к плану зонирования участка и даже подложить его под лист кальки с модульной сеткой вместо масштабного плана. На плане зонирования видны площади, отведенные под то или иное использование, и указано, сколько квадратов модульной сетки они занимают.
Первый пробный вариант удобно выполнить в так называемой прямоугольной теме, используя в качестве основы рисунка геометрические фигуры – прямоугольники и квадраты. Геометрические фигуры, легко вписываются в линии модульной сетки, помогут впоследствии легко придать ландшафтный рисунок, вычертив полуокружности вместо прямых углов и волнистые линии – вместо прямых. Важно, что при этом сохранятся не только принципиальная планировка, но и пропорции плоских фигур плана.
Также можно выполнить пробный вариант в круговой теме или диагональной. Для последней можно перечертить сетку, ориентировав её линии и квадраты под углом 45 гр. к дому.
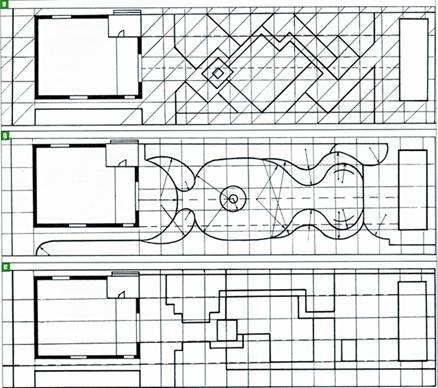
Зато наиболее выигрышно смотрятся так называемые "полные" геометрические и абстрактные фигуры: окружность, овал, квадрат, прямоугольник и абстрактные фигуры, схожие по форме с прямоугольником или с окружностью.
В практике садового строительства получили распространение несколько плоских фигур, к которым можно свести практически любой проект. Как правило, они интерпретируются как " формы газона", т.е. фигуры плоского плана, обозначающие границы газона в саду. Однако они могут быть использованы и как фигуры мощения, водоемов, цветников.
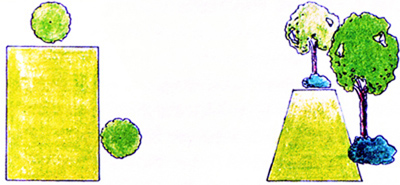
"Прямоугольник" Классическая форма газона, наиболее распространена в регулярных садах.
Получение прямого угла (рис. 75). На прямой линии АБ из среднего пункта В в стороны к точкам А и Б отмеряют по равной части, получая точки Д u E. Затем из точек Д и Е описывают две перекрещивающиеся между собой дуги, причем в месте перекрещивания дуг получается точка Г. Тогда точку Г соединяют прямой линией с точкой В и получают прямой угол.
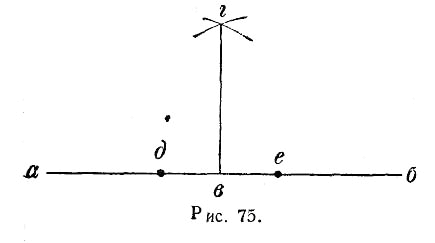
Другой способ получения прямого угла состоит в том, что проводят основную прямую линию БВ (рис. 76) и из точки А описывают дугу, причем в местах пересечения дуги с прямой линией БВ получаются точки Д и Е. Тогда линию эту делят пополам, получают срединную точку Г и соединяют ее с точкой А. Получается прямой угол, или перпендикуляр к прямой БВ.