Магические квадраты…От этого словосочетания сразу веет волшебством и таинственностью. Еще с в древности ученые увидели, что числа имеют свою самостоятельную жизнь, свои тайны.
Магический квадрат - это квадратная таблица, заполненная различными числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Среди несложных магических квадратов по математике выделяют разновидности чётного и нечётного порядка.
Первые подобные таблицы использовались ещё в Древней Греции и Китае. Это подтверждено археологическими находками. Арабы называли квадраты магическими, так как верили, что они обладают волшебными свойствами и могут защитить от многих напастей.
В середине XVI века вопросом о том, как работает магический квадрат, заинтересовались математики в Европе. Они начали активно исследовать загадочные сочетания цифр. Учёные стремились вывести общие принципы построения квадратов и найти всё множество возможных вариантов. В 19 и 20 веках интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры и операционного исчисления.
С давних пор математики стремились решить две основные задачи, связанные с магическими квадратами: найти общий метод их построения и описать все возможные магические квадраты. Для каждого вида квадрата были найдены свои способы решения задачи. Пока не известен общий, пригодный для квадратов любого порядка, метод их построения. Вторая задача также до сих пор не решена. Отчасти это связано с тем, что с увеличением порядка квадрата число магических квадратов стремительно растет.
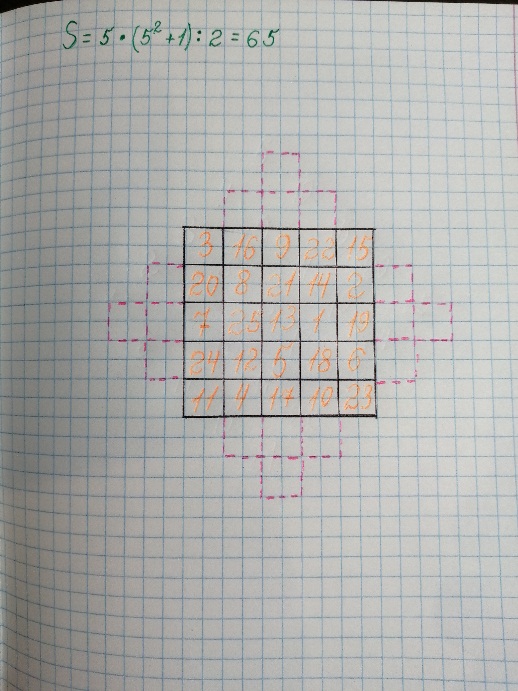
Каждый элемент магического квадрата называется клеткой. Квадрат, сторона которого состоит из n клеток, содержит n2 клеток и называется квадратом n-го порядка. Сумма S чисел, стоящих в каждой строке, каждом столбце и на любой диагонали, называется магической постоянной квадрата и равна S = n*(n2 + 1)/2.
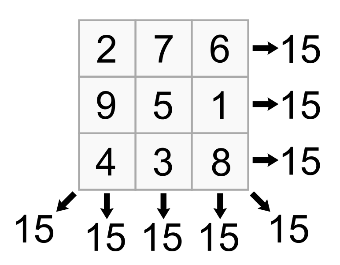
Рассмотрим первый пример. Доказано, что из всех существующих комбинаций квадратов нечетного порядка 3х3, только одна комбинация является магической. Как же ее найти?
1. Найдем магическую постоянную квадрата S=3*(32+1)/2=15
2. Число 15 представим в виде суммы троек натуральных чисел от 1 до 9. Таких комбинаций 8.
1 + 5 + 9 2 + 6 + 7 2+ 4+ 9 3 + 5 + 7
2 + 5 + 8 4 + 5 + 6 1 + 6 + 8 3 + 4 + 8
3. Замечаем, что число 5 входит сразу в четыре суммы. Значит, содержащая его клетка должна находиться на пересечении четырех прямых рядов. В квадрате размером 3x3 этому условию удовлетворяет только одна клетка – центральная.
4. Любые два числа, попавшие в одну тройку с числом 5, должны размещаться симметрично относительно центра квадрата. Каждое четное число встречается сразу в трех суммах, поэтому четные числа должны попасть в клетки, лежащие на пересечении трех рядов, то есть в углах таблицы. Наконец, каждое из оставшихся нечетных чисел входит в суммы дважды, их место - в средних клетках по краям квадрата. Следуя найденным принципам, легко распределить все девять чисел.
 Рассмотрим второй пример.
Рассмотрим второй пример.
Для быстрого составления магических квадратов нечетного порядка существует метод террас.
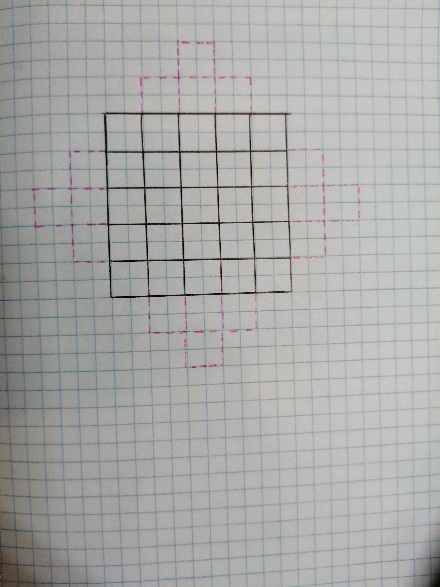
1. Начертим таблицу, например 5х5.
2. К таблице с каждой стороны достроим пирамидки (террасы), как показано на рисунке
3. Начинаем заполнять квадрат с левой вершины пирамидки, двигаемся вверх по диагонали. Квадрат заполняем числами с 1 до 25 (n2). Получаем заполненную фигуру, как показано на рисунке
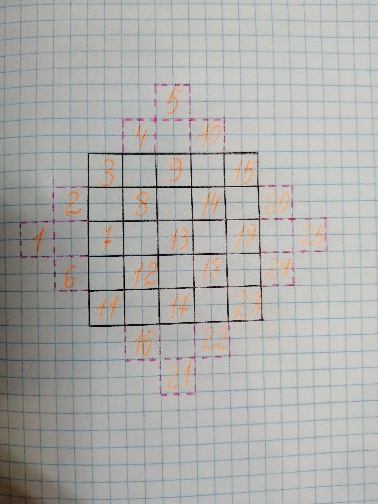
4. Далее заполняем пустые клетки квадрата таким образом: каждое число, расположенное в пирамидках, «двигаем» в сторону квадрата на число клеток, которое равно порядку квадрата (в нашем примере это число 5)
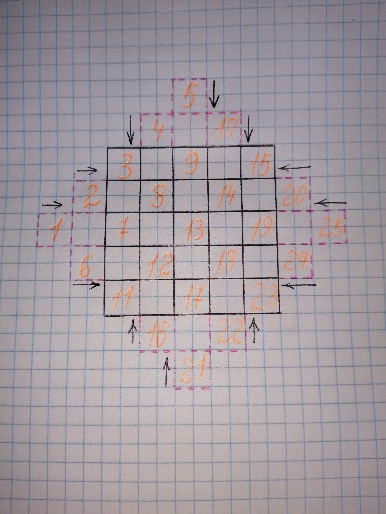
5. Получаем заполненный магический квадрат. Проверяем правильность составления квадрата через формулу магической постоянной. Наш квадрат составлен верно. Данным способом можно составить любой квадрат нечетного порядка.