НАДЕЖНОСТЬ СИСТЕМ ЭЛЕКТРОСнАБЖЕНИЯ
Учебно-методическое пособие для студентов заочников отделения по специальности
140211 «Электроснабжение»
Нижнекамск
Составитель В.М. Булатова
Надежность систем электроснабжения: методические указания для выполнения контрольных работ / В.М. Булатова – 50 с.
Методические указания соответствуют требованиям государственного образовательного стандарта высшего профессионального образования.
Предназначены для студентов заочного отделения, обучающихся по специальности 140211 «Электроснабжение»
Печатаются по решению редакционно-издательского совета Нижнекамского химико-технологического института.
Рецензенты;
Гл. энергетик ОАО «НКНХ» А.М. Вдовин
Д.п.н., профессор С.С. Амирова
© Нижнекамский химико-технологический институт, 2008
Глава 1. Количественные характеристики основных показателей надежности
Свойства надежности
Надежность систем электроснабжения (СЭС) – свойство СЭС выполнять заданные функции в заданном объеме при определенных условиях функционирования.
Безотказность – свойство объекта непрерывно сохранять работоспособность в течение некоторого времени.
Долговечность – свойство объекта сохранять работоспособность длительно, с возможными перерывами на ремонт, вплоть до разрушения или другого предельного состояния (например, по условиям безопасности).
Ремонтопригодность – свойство объекта, заключающееся в его приспособленности к предупреждению и обнаружению причин возникновения отказов, повреждений и устранению их последствий.
Функция реакции – свойство СЭС или потребления реагировать на изменение напряжения в зависимости от их величины и продолжительности.
Количественные характеристики основных показателей надежности
Рассматриваемые здесь показатели применяются для оценки надежности как невосстанавливаемых (одноразового использования), так и подлежащих ремонту, т.е. восстанавливаемых объектов до появления первого отказа.
Вероятность безотказной работы Р(t) – вероятность того, что в заданном интервале времени (0;t) в системе или элементе не произойдет отказ.
Статистически Р(t) определяется как отношение числа элементов N(t), безотказно проработавших до момента t, к первоначальному числу наблюдаемых элементов N(0):
P(t) = N(t) / N(0). (1.1)
Число работоспособных в течение времени (0, t) элементов будет:
N(t) = N(0) – n(0,t) (1.2)
где n(0,t) – число отказавших за время (0,t) элементов.
Очевидно, что
0 ≤ Р(t) ≤ 1, P(0) =1, P(∞) = 0.
Вероятность появления отказа Q(t) – вероятность того, что в заданном интервале времени (0, t) произойдет отказ.
Статистическая оценка Q(t):
Q(t) = n(0,t) / N(0) (1.3)
Таким образом, всегда имеет место соотношение
Р(t) + Q(t) = 1. (1.4)
Частота отказов а(t) – производная от вероятности появления отказа, означающая вероятность того, что отказ элемента произойдет за единицу времени (t, t + ∆t).
(1.5)
Для определения величины a(t) можно использовать статистическую оценку:
, (1.6)
где n(t,∆t) – число элементов, отказавших в интервале времени от t до t + ∆t.
Точность статистической оценки (1.6) возрастает с увеличением первоначального числа наблюдаемых элементов и уменьшением временного интервала ∆t.
Частота отказов, вероятность безотказной работы и вероятность появления отказа связаны следующими зависимостями:
, (1.7)
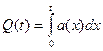. (1.8)
Интенсивность отказов λ(t) – условная вероятность отказа после момента t за единицу времени ∆t при условии, что до момента t отказа элемента не было.
Интенсивность отказов связана с частотой отказов и вероятностью безотказной работы:
(1.9)
Так как P(t) ≤ 1, то всегда выполняется соотношение λ(t) ≥ a(t).
Статистически интенсивность отказов определяется таким образом:
. (1.10)
Различие между частотой и интенсивностью отказов в том, что первый показатель характеризует вероятность отказа за интервал (t, t + ∆t) элемента, взятого из группы элементов произвольным образом, причем неизвестно, в каком состоянии (работоспособном или неработоспособном) находится выбранный элемент. Второй показатель характеризует вероятность отказа за тот же интервал времени элемента, взятого из группы оставшихся работоспособными к моменту t элементов.
Отметим важную особенность, вытекающую из формулы (1.9) для высоконадежных элементов и систем: если P(t) ≥ 0,99, то a(t) ≈ λ(t). Поэтому в практических расчетах возможна при указанном условии взаимная замена a(t) и λ(t).
Интегрируя выражение (1.9), получаем формулу для определения вероятности безотказной работы в зависимости от интенсивности отказов и времени:
. (1.11)