О. А. ЗАБЛОЦКАЯ, Л. С. ПЕТРОВА, А. М. СОКОЛЬНИКОВА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИЗУЧЕНИЮ РАЗДЕЛА
«КРАТНЫЕ ИНТЕГРАЛЫ. ТЕОРИЯ ПОЛЯ»
Омск 2008
Министерство путей сообщения Российской Федерации
Федеральное агентство железнодорожного транспорта
Омский государственный университет путей сообщения
_________________
О. А. Заблоцкая, Л. С. Петрова, А. М. Сокольникова
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИЗУЧЕНИЮ РАЗДЕЛА «Кратные интегралы. теория поля»
Утверждено редакционно-издательским советом университета
Омск 2008
УДК 517.37(075.8)
ББК 22.161.12я73
З−12
Методические указания к изучению раздела «Кратные интегралы. Теория поля»:Методические указания по высшей математике / О. А. Заблоцкая, Л. С. Петрова, А. М. Сокольникова; Омский гос. ун-т путей сообщения. Омск, 2008. 45 с.
Методические указания предназначены для изучения данного раздела курса математики и закрепления навыков решения задач студентами. В первой главе указаний приводятся подробные решения задач, встречающихся в типовом расчете. Вторая глава содержит 30 вариантов заданий. Каждый вариант состоит из 11 задач, содержание которых охватывает практически все основные вопросы программы втуза, связанные с темой «Кратные интегралы. Теория поля».
Предназначены для студентов второго курса технических специальностей очной формы обучения.
Библиогр.: 5 назв., рис. 10.
Рецензенты: доктор физ.-мат. наук И.И.Гончар,
канд. пед. наук Е. И. Федорова.
_______________________________
ÓОмский гос. университет
путей сообщения, 2008
СОДЕРЖАНИЕ
1. Введение............................................................................................ 5
2. Методические указания по решению типовых заданий.................. 6
3. Варианты типовых заданий для самостоятельной работы............. 16
Библиографический список................................................................... 44
ВВЕДЕНИЕ
Математическую основу раздела учебного курса математики «Кратные интегралы. Теория поля» составляет интегрирование скалярных и векторных функций векторного аргумента. Настоящие методические указания имеют целью помощь студентам при освоении техники интегрирования и иллюстрацию физических приложений указанной темы. Они содержат варианты индивидуальных заданий для студентов очной формы обучения.
В первой части приводятся подробные решения типовых задач по рассматриваемой теме. Однако объем методических указаний не позволяет поместить в них разбор всех видов каждого типа задач. Поэтому авторы рекомендуют при выполнении индивидуальных заданий обратить внимание на библиографический список и воспользоваться, в частности, источниками [1, 3, 5].
1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РЕШЕНИЮ ТИПОВЫХ ЗАДАНИЙ
Задача 1. Изменить порядок интегрирования в повторном интеграле  .
.
Решение. Область интегрирования D ограничена линиями, имеющими уравнения  ,
,  ,
,  ,
,  и изображенными на рис.1.
и изображенными на рис.1.

|

|
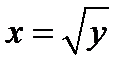
|

|

|

|
| Рис. 1 |
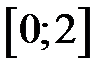 . Заметим, что для
. Заметим, что для  и
и  точки выхода из области D лежат на линиях, которые задаются различными уравнениями: для
точки выхода из области D лежат на линиях, которые задаются различными уравнениями: для  линией выхода является парабола
линией выхода является парабола  , а для
, а для  − прямая
− прямая  . Следовательно, область D надо разбить на две области
. Следовательно, область D надо разбить на две области  и
и 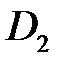 прямой
прямой  , параллельной оси Ох (рис.1).
, параллельной оси Ох (рис.1).
Используя свойства интеграла по области, получим

Задача 2. Вычислить повторный интеграл  .
.
Решение. Сначала вычисляем внутренний интеграл, где х является переменной величиной, а у − постоянной. Затем полученный результат интегрируем по переменной у:


Задача 3. Найти массу пластины, ограниченной линиями у =2, у =4, х =0, х=у, если в каждой ее точке поверхностная плотность  .
.
Решение. Масса пластины вычисляется по формуле

|

|
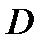
|

|

|
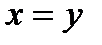
|
| Рис. 2 |

где D − область, которую занимает пластина (рис.2). Для вычисления двойного интеграла перейдем к интегралу повторному, при этом предпочтительным является следующий порядок интегрирования: внутреннее интегрирование по переменной х, внешнее − по у (иначе для определения массы пришлось бы вычислять два повторных интеграла вместо одного).

Задача 4. Найти площадь области, ограниченной линиями  ,
,  .
.
| -4 |
| -4 |

|

|

|

|

|
| Рис. 3 |
 .
.
Чертеж области D изображен на рис.3. Чтобы не разбивать область на две и не вычислять два повторных интеграла вместо одного, выбираем следующий порядок интегрирования: внутреннее интегрирование по переменной х, внешнее − по у. Находим пределы интегрирования и вычисляем площадь:

Задача 5. Перейдя к полярной системе координат, вычислить интеграл  , если D − область, ограниченная линиями
, если D − область, ограниченная линиями 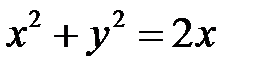 ,
, 
 .
.

|

|

|

|

|
| Рис. 4 |
 ,
,  , перепишем уравнение линии
, перепишем уравнение линии 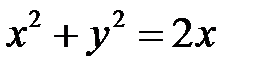 в виде
в виде  . Это окружность радиуса
. Это окружность радиуса  с центром в точке (1; 0) (рис.4). Переходя к полярной системе, получим
с центром в точке (1; 0) (рис.4). Переходя к полярной системе, получим  ,
,  .
.

Задача 6. Вычислить объем тела, ограниченного поверхностями  ,
,  ,
, 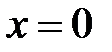 ,
,  ,
,  .
.

|

|

|
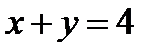
|

|
| Рис. 5 |

|

|

|

|
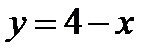
|
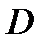
|
| Рис. 6 |
 − параболоидом вращения. Объем такого тела вычисляется по формуле
− параболоидом вращения. Объем такого тела вычисляется по формуле 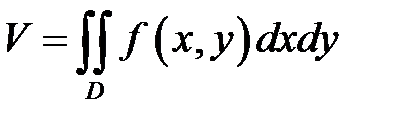 . Найдем значение объема данного тела.
. Найдем значение объема данного тела.

Задача 7. Найти массу тела Т, ограниченного поверхностями  ,
, 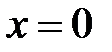 ,
,  ,
,  , если плотность меняется по закону
, если плотность меняется по закону 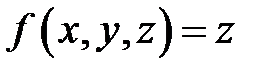 .
.
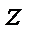
|

|

|

|

|
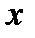
|

|

|

|
| Рис. 7 |

|

|

|

|

|
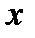
|

|

|
| Рис. 8 |
Решение. Масса тела вычисляется по формуле
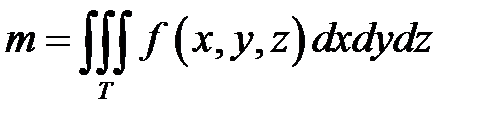 , где плотность
, где плотность 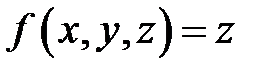 . Тело Т изображено на рис.7, а плоская область интегрирования
. Тело Т изображено на рис.7, а плоская область интегрирования 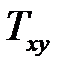 − на рис.8.
− на рис.8.

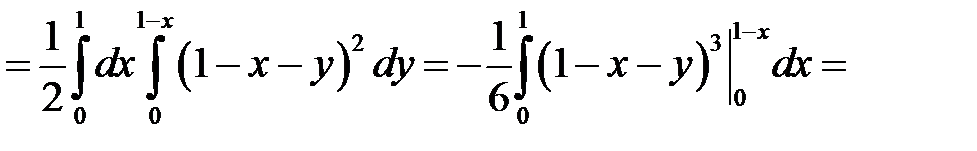

Задача 8. Вычислить 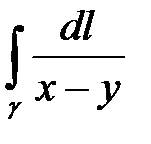 , где
, где  − отрезок прямой, соединяющий точки
− отрезок прямой, соединяющий точки  и
и  .
.
Решение. Пользуясь уравнением прямой, проходящей через две точки  , получим уравнение линии интегрирования – прямой
, получим уравнение линии интегрирования – прямой  :
:  .Так как
.Так как  , то
, то 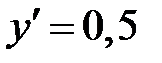 ,
,  . Тогда
. Тогда  . Вычислим криволинейный интеграл:
. Вычислим криволинейный интеграл:

Задача 9. Вычислить работу силового поля  вдоль дуги параболы
вдоль дуги параболы 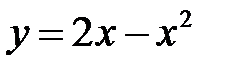 от точки
от точки  до точки
до точки  .
.
Решение. Работа силового поля  вдоль дуги MN вычисляется с помощью криволинейного интеграла второго рода по формуле
вдоль дуги MN вычисляется с помощью криволинейного интеграла второго рода по формуле 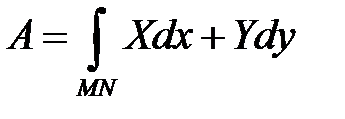 , где
, где  ,
,  . Найдем пределы интегрирования: началу дуги MN соответствует
. Найдем пределы интегрирования: началу дуги MN соответствует 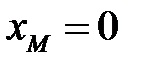 , концу
, концу  . Учитывая, что
. Учитывая, что  и
и  , получаем интеграл
, получаем интеграл

Задача 10. Найти циркуляцию вектора  вдоль контура АВСА, получаемого при пересечении параболоида
вдоль контура АВСА, получаемого при пересечении параболоида 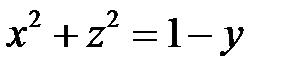 с координатными плоскостями (рис.9). Решить задачу с помощью непосредственного вычисления циркуляции и с помощью формулы Стокса.
с координатными плоскостями (рис.9). Решить задачу с помощью непосредственного вычисления циркуляции и с помощью формулы Стокса.

|

|

|

|
|
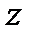
|

|

|

|

|
| Рис. 9 |
 .
.  ,
,  . Циркуляция вектора вычисляется по формуле
. Циркуляция вектора вычисляется по формуле  Полученные криволинейные интегралы вычислим последовательно.
Полученные криволинейные интегралы вычислим последовательно.
а) На АВ  и
и  , следовательно,
, следовательно, 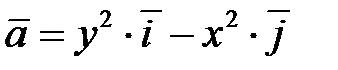 . Парабола АВ имеет уравнение
. Парабола АВ имеет уравнение  . Отсюда
. Отсюда  ,
, 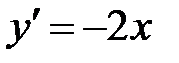 . При перемещении по дуге АВ от точки А до точки В значение х убывает от 1 до 0. Таким образом,
. При перемещении по дуге АВ от точки А до точки В значение х убывает от 1 до 0. Таким образом,
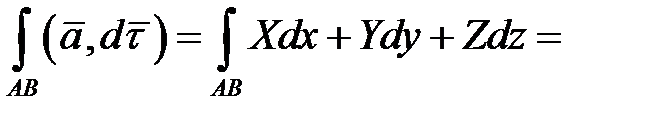

б) На ВС  ,
, 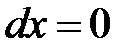 ,
, 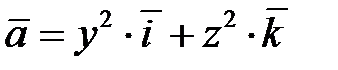 . Парабола ВС имеет уравнение
. Парабола ВС имеет уравнение  . При перемещении по дуге ВС от точки В до точки С переменная z возрастает от 0 до 1. Следовательно,
. При перемещении по дуге ВС от точки В до точки С переменная z возрастает от 0 до 1. Следовательно,

в) На СА  ,
,  ,
,  . СА − дуга окружности
. СА − дуга окружности  , причем при перемещении от точки С в точку А переменная z убывает от 1 до 0. Следовательно,
, причем при перемещении от точки С в точку А переменная z убывает от 1 до 0. Следовательно,

Таким образом, 
2) Вычислим циркуляцию с помощью формулы Стокса в координатной форме 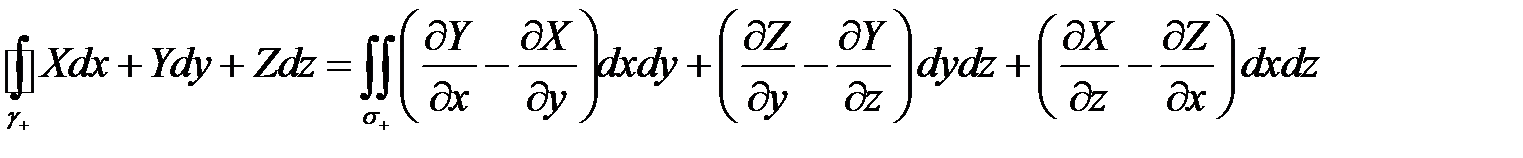 . В качестве поверхности
. В качестве поверхности  можно взять, например, часть поверхности параболоида, ограниченную контуром АВСА. При этом берется верхняя её сторона, т.к. с конца нормали к этой стороне обход контура виден совершающимся против часовой стрелки. Учитывая, что
можно взять, например, часть поверхности параболоида, ограниченную контуром АВСА. При этом берется верхняя её сторона, т.к. с конца нормали к этой стороне обход контура виден совершающимся против часовой стрелки. Учитывая, что  ,
,  ,
,  ,
,  ,
,  ,
,  получаем интеграл
получаем интеграл
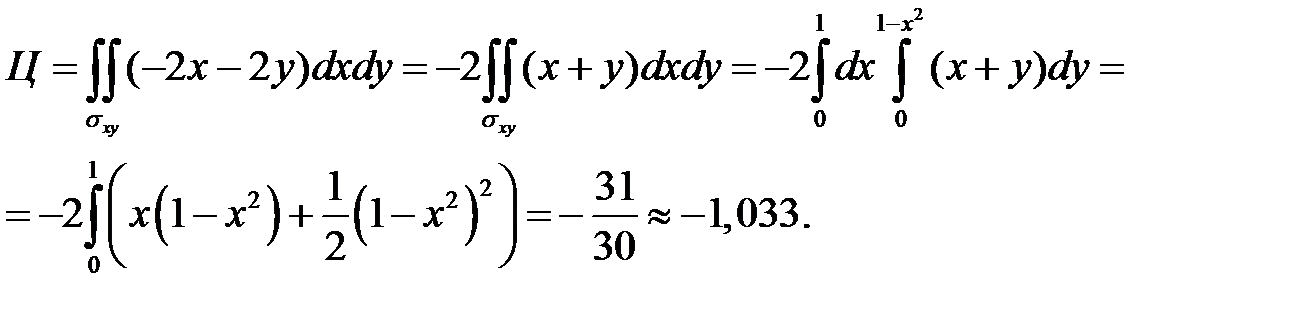

|

|

|

|
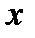
|
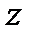
|

|
| Рис. 10 |
Задача 11. Вычислить поток векторного поля  через внешнюю сторону поверхности пирамиды, ограниченной
через внешнюю сторону поверхности пирамиды, ограниченной
плоскостью 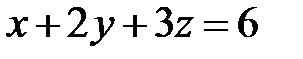 и координатными
и координатными
плоскостями (рис.10): 1) непосредственно; 2) с помощью теоремы Остроградского− Гаусса.
Решение. 1) Поверхность пирамиды ОАВС
состоит из треугольников АОВ, АОС, ВОС и АВС. Следовательно, искомый поток есть сумма потоков через поверхности этих треугольников, причем берется та их сторона, которая является внешней для пирамиды.
а) Вычислим поток через поверхность треугольника АВС:
 .
.
Для интеграла  независимыми переменными являются у и z. Проекцией
независимыми переменными являются у и z. Проекцией  поверхности
поверхности  на координатную плоскость
на координатную плоскость  будет треугольник ВОС. Преобразуем подынтегральную функцию, выразив х через у и z из уравнения поверхности
будет треугольник ВОС. Преобразуем подынтегральную функцию, выразив х через у и z из уравнения поверхности  :
:  . Вектор нормали
. Вектор нормали  к выбранной стороне поверхности образует с осью Ох острый угол, поэтому при переходе от поверхностного интеграла второго рода к двойному берем знак «+». Получаем:
к выбранной стороне поверхности образует с осью Ох острый угол, поэтому при переходе от поверхностного интеграла второго рода к двойному берем знак «+». Получаем:

Для интеграла  независимыми переменными являются х и z. Проекцией
независимыми переменными являются х и z. Проекцией  поверхности
поверхности  на координатную плоскость
на координатную плоскость  будет треугольник АОС. Подынтегральная функция не содержит зависимой переменной у, поэтому преобразовываться не будет. Вектор нормали
будет треугольник АОС. Подынтегральная функция не содержит зависимой переменной у, поэтому преобразовываться не будет. Вектор нормали  к выбранной стороне поверхности образует с осью Оу острый угол, поэтому при переходе от поверхностного интеграла второго рода к двойному берем знак «+».
к выбранной стороне поверхности образует с осью Оу острый угол, поэтому при переходе от поверхностного интеграла второго рода к двойному берем знак «+».
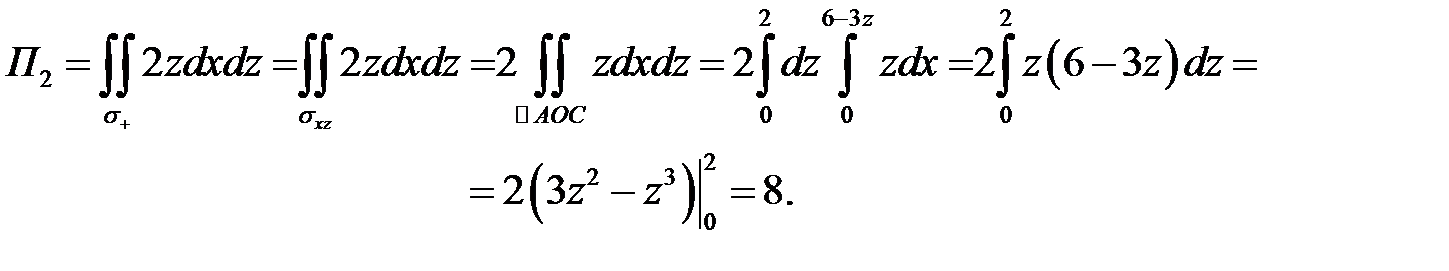
Для интеграла 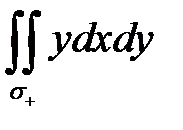 независимыми переменными являются х и у. Проекцией
независимыми переменными являются х и у. Проекцией  поверхности
поверхности  на координатную плоскость
на координатную плоскость 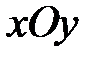 будет треугольник АОВ. Подынтегральная функция не содержит зависимой переменной z. Вектор нормали
будет треугольник АОВ. Подынтегральная функция не содержит зависимой переменной z. Вектор нормали  образует с осью Оz острый угол. Следовательно,
образует с осью Оz острый угол. Следовательно,
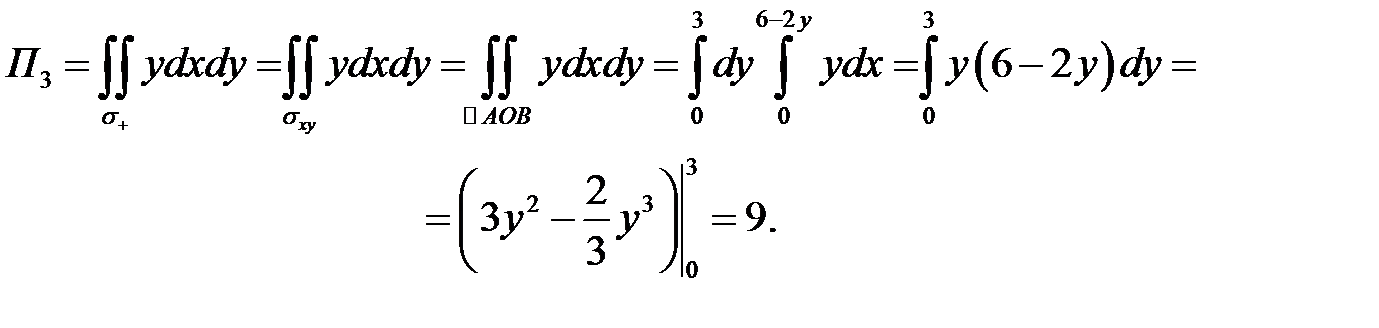
Таким образом, 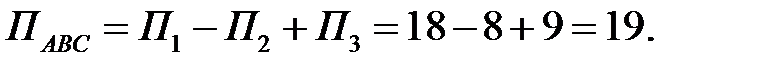
б) Вычислим поток через поверхности треугольников АОВ, АОС, ВОС.
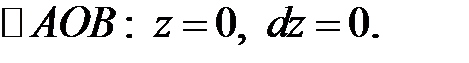 Поэтому:
Поэтому:


 Следовательно,
Следовательно,

 Тогда:
Тогда:

Суммируя все вычисленные потоки, получаем:

2) Формула Остроградского− Гаусса имеет следующий вид:
 , где
, где  , Т − тело, ограниченное поверхностью
, Т − тело, ограниченное поверхностью 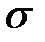 .
.
Чтобы воспользоваться этой формулой, возьмем в качестве тела Т область, ограниченную поверхностью пирамиды АОВС.

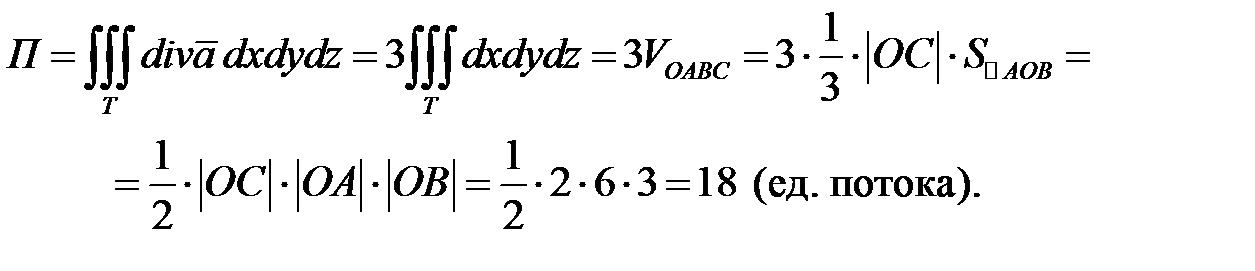
2. Варианты типовых заданий для самостоятельной работы
Задача 1. Изменить порядок интегрирования. Область интегрирования изобразить на чертеже.
1. а) 
| б) 
|
2. а) 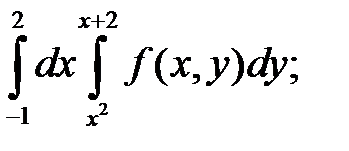
| б) 
|
3. а) 
| б) 
|
4. а) 
| б) 
|
5. а) 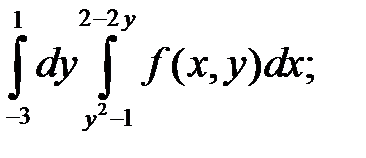
| б) 
|
6. а) 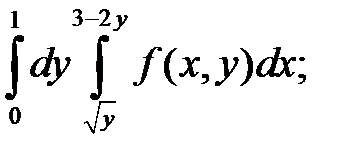
| б) 
|
7. а) 
| б) 
|
8. а) 
| б) 
|
9. а) 
| б) 
|
10. а) 
| б) 
|
11. а) 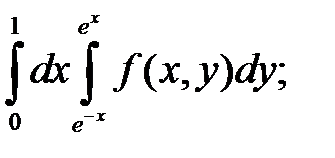
| б) 
|
12. а) 
| б) 
|
13. а) 
| б) 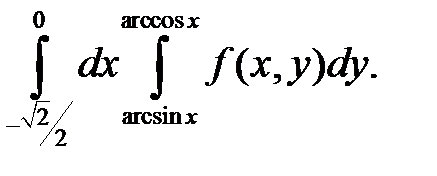
|
14. а) 
| б) 
|
15. а) 
| б) 
|
16. а) 
| б) 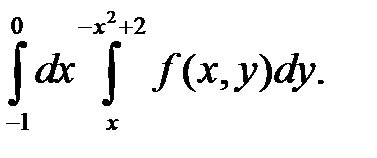
|
17. а) 
| б) 
|
18. а) 
| б) 
|
19. а) 
| б) 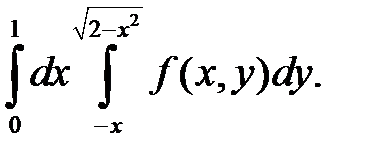
|
20. а) 
| б) 
|
21. а) 
| б) 
|
22. а) 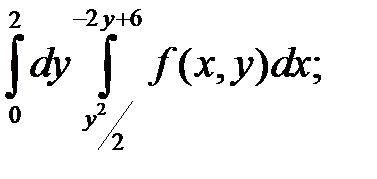
| б) 
|
23. а) 
| б) 
|
24. а) 
| б) 
|
25. а) 
| б) 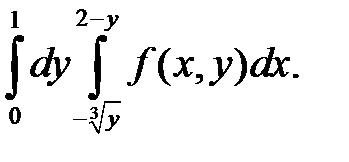
|
26. а) 
| б) 
|
27. а) 
| б) 
|
28. а) 
| б) 
|
29. а) 
| б) 
|
30. а) 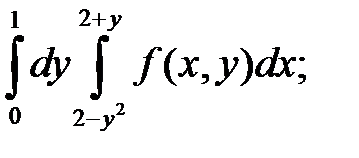
| б) 
|
Задача 2. Вычислить: а) повторный интеграл; б) двойной интеграл по области D, ограниченной данными линиями.
1. а) 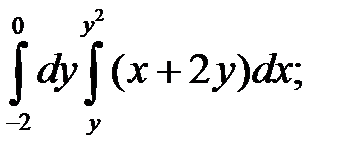 б)
б)  D:
D: 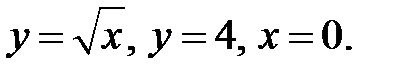
2. а)  б)
б)  D:
D: 
3. а)  б)
б) 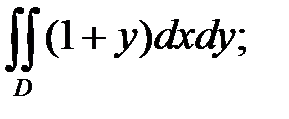 D:
D: 

4. а)  б)
б)  D:
D: 
5. а)  б)
б)  D:
D: 
6. а)  б)
б) 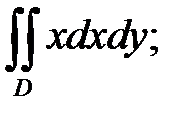 D:
D: 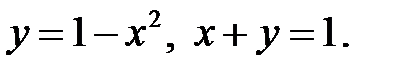
7. а)  б)
б)  D:
D: 
8. а)  б)
б)  D:
D: 
9. а)  б)
б)  D:
D: 
10. а)  б)
б)  D:
D: 
11. а)  б)
б) 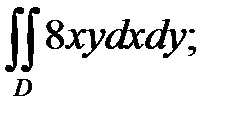 D:
D: 
12. а)  б)
б)  D:
D: 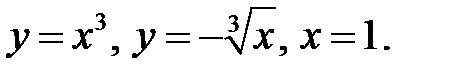
13. а)  б)
б)  D:
D: 
14. а)  б)
б) 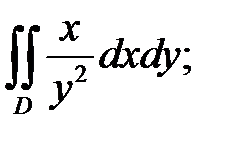 D:
D: 
15. а)  б)
б)  D:
D: 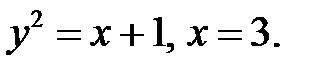
16. а)  б)
б)  D:
D: 
17. а)  б)
б) 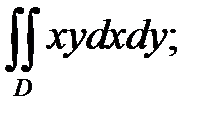 D:
D: 
18. а)  б)
б) 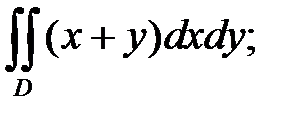 D:
D: 
19. а)  б)
б)  D:
D: 
20. а)  б)
б)  D:
D: 
21. а)  б)
б)  D:
D: 
22. а)  б)
б) 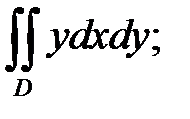 D:
D: 
23. а) 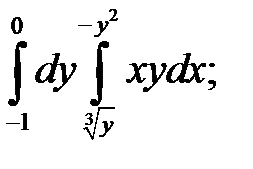 б)
б)  D:
D: 
24. а)  б)
б)  D:
D: 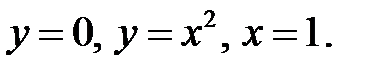
25. а)  б)
б) 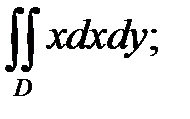 D:
D: 
26. а) 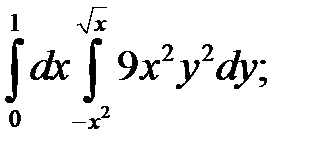 б)
б)  D:
D: 
27. а)  б)
б)  D:
D: 
28. а) 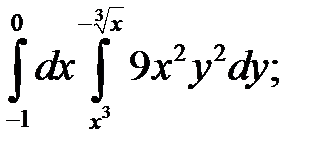 б)
б)  D:
D: 
29. а)  б)
б)  D:
D: 
30. а)  б)
б)  D:
D: 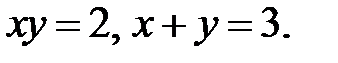
Задача 3. Найти массу пластины D, ограниченной данными линиями и имеющей поверхностную плотность 
1. D:  а)
а)  б)
б) 
2. D:  а)
а) 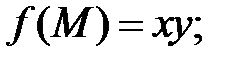 б)
б) 
3. D:  а)
а)  б)
б) 
4. D:  а)
а)  б)
б) 
5. D:  а)
а) 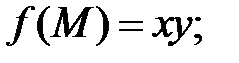 б)
б) 
6. D:  а)
а)  б)
б) 
7. D: 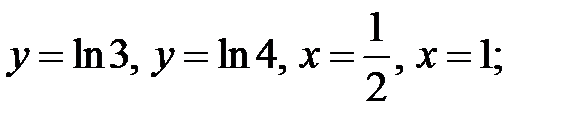 а)
а)  б)
б) 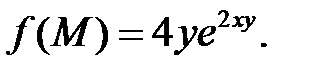
8. D:  а)
а)  б)
б) 
9. D:  а)
а)  б)
б) 
10. D:  а)
а)  б)
б) 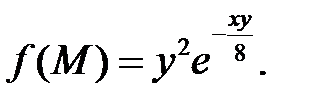
11. D:  а)
а)  б)
б) 
12. D:  а)
а) 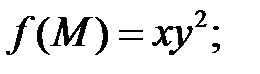 б)
б) 
13. D:  а)
а)  б)
б) 
14. D:  а)
а)  б)
б) 
15. D:  а)
а)  б)
б) 
16. D: