Образцы задач к билетам по линейной алгебре (ФББ, 2017-18)

1. В ортонормированном базисе даны векторы . Найти вектор такой, что .
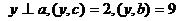2. Найти площадь параллелограмма, построенного на векторах , если .
3. Даны вершины треугольника A(–5,3), B(7,8), C(–2,–1). Составить уравнения медианы, биссектрисы и высоты треугольника, проведенных из вершины А. (Система координат ортонормированная)

(Ответ: медиана , биссектриса , высота )

1. Даны точки . Найти: (а) объем пирамиды EFGH; (б) длину высоты, проведенной из вершины H, в) расстояние между прямыми (EF) и (GH).
2. Точки A(1,-2,3), B(3,2,1), C(6,4,4) – вершины параллелограмма. Определите координаты его четвертой вершины (найдите все решения).(D₁(4,0,6), D₂(8,9,2), D₃(–5,–4,0)).
3. Составьте уравнение плоскости, проходящей через точку M(1,0,3) и перпендикулярной к плоскостям .
4. Докажите, что прямые пересекаются, и составьте уравнение содержащей их плоскости.
5. Точка А лежит на прямой и удалена от плоскости 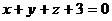на расстояние . Найдите координаты точки А.
6. а) Найдите угол между плоскостью и прямой ; б) составьте уравнения ортогональной проекции данной прямой на данную плоскость.
7. Составьте параметрические и канонические уравнения прямой, по которой пересекаются плоскости .
8. Даны прямые и . а) найдите угол между a и b; б) вычислите расстояние между a и b.

12. Найдите матрицу X, удовлетворяющую уравнению 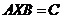, где .

1. Найти ранг матрицы, указать базисные столбцы и выразить через них остальные столбцы.
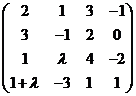2. Найдите ранг матрицы в зависимости от параметра .
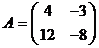3. Найдите собственные значения и собственные векторы линейного оператора, заданного матрицей а) , б) , в) (при всевозможных значениях параметра). Если возможно, приведите ее к диагональному виду (нужно указать диагональный вид и базис, в котором матрица имеет такой вид).
4. Найдите собственные значения и собственные векторы линейного оператора, заданного матрицей . Можно ли из них выбрать базис? Если да, указать такой базис и записать в нем матрицу оператора.
5. Решите неравенство .
6. Обратите матрицу .
7. Найти общее решение данной системы уравнений, представить его в виде суммы частного решения и линейной комбинации фундаментальной системы решений соответствующей однородной системы уравнений: .
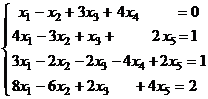8. а) Найти размерность и базис линейной оболочки векторов в .

б) Составить систему однородных линейных уравнений, задающую это подпространство.

1. В базисе 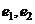линейный оператор f имеет матрицу . Найти матрицу этого оператора в базисе .
2. Найти матрицу линейного отображения, переводящего векторы соответственно в векторы . Определить размерности и базисы ядра и образа этого отображения.
3. Вычислить матрицу перехода от базиса к базису 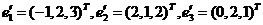в линейном пространстве R³ и определить координаты вектора в базисе .
4. Линейный оператор на двумерной плоскости векторов (приложенных в начале координат) переводит любой вектор в его ортогональную проекцию на прямую . Запишите его матрицу в данном ортонормированном базисе, найдите собственные значения и собственные векторы.
5. Привести квадратичную форму: а) ;

б) к каноническому (нормальному) виду методом Лагранжа, определить ее ранг и индексы инерции.

1. Исследовать квадратичную форму на положительную и отрицательную определенность в зависимости от параметра α: .
2. Построить при помощи процесса ортогонализации ортонормированный базис линейной оболочки векторов (стандартный базис ортонормированный).
3. Найти ортонормированный базис из собственных векторов линейного оператора, заданного в ортонормированном базисе матрицей: а) , б) ; привести матрицу к диагональному виду;
4. Привести квадратичную форму

к главным осям (диагональному виду) посредством ортогональной замены координат.

1. Доказать, что пространство R⁴ является прямой суммой подпространств , и разложить вектор в сумму проекций на эти подпространства, где .