1.1 Определение пропускной способности трубопровода.
Запишем уравнение Бернулли для начального I-I и конечного II-II сечений трубопровода.
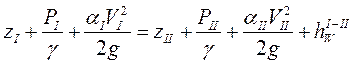
Для нашего случая примем значение коэффициента Кориолиса равным единице. aI = aII = 1. Геометрический напор ZI = Н1+h. ZII = H2.
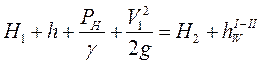
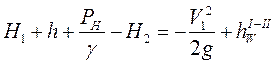
где 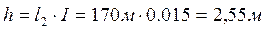 ,
,

Пусть Н0 равно:
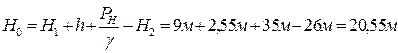
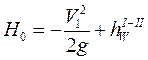 (1)
(1)
Составим сумму всех потерь.
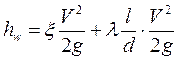
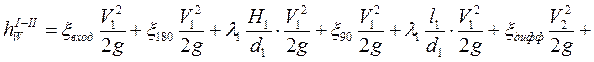
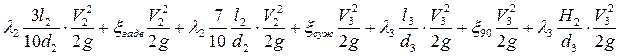
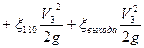
Выразим все скорости через V1:
 ;
; 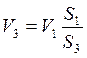 где
где
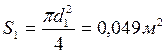 ;
; 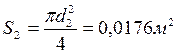 ;
; 
Учитывая это выражение (1) примет вид
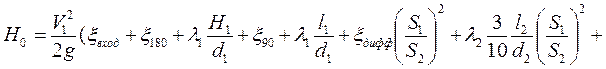
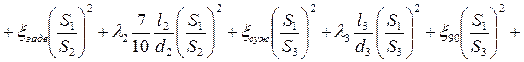
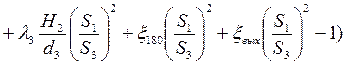 (2)
(2)
Отсюда:

Найдём коэффициенты местных потерь.
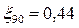

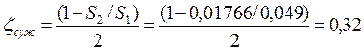
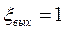
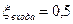
Рассчитаем коэффициент местных потерь конфузора:
По формуле 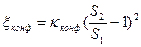 , где кдиф зависит от угла θ.
, где кдиф зависит от угла θ.
Вычислим кконф:
Длина промежутка расширения равна 0.5 м.
Вычислим тангенс угла θ/2
tg θ/2 = (d2-d1)/0.5
Вычислим арктангенс угла θ=5,49о
При этом значении угла θ выбираем значение кконф=0,13
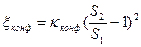 =0,413
=0,413
а) Задвижка открыта.
ξзадв = 4
Предполагаем во всех трубах IV зону сопротивления. При этом
 , kэк – абсолютная величина так называемой эквивалентной равномерно-зернистой шероховатости.
, kэк – абсолютная величина так называемой эквивалентной равномерно-зернистой шероховатости.
Так как трубы чугунные, неновые, то kэк=1мм.
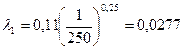
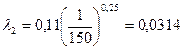
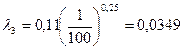
По формуле (2) рассчитываем скорость жидкости в первой трубе.
V1 = 0,401331 м/с
V2 = V1(S1/S2) =1,117343 м/с
V3 = V1(S1/S3) =2,505125 м/с
Определим расход жидкости по формуле Q = V1*ω1 = 0,019665 м3/с.
Выполним проверку правильности предположения о наличии четвертой области сопротивления на всех трех участках трубопровода. Для этого необходимо вычислить для каждого из участков числа Рейнольдса по уравнению
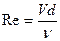
и сравнить полученные значения Re с граничным числом Рейнольдса, вычисленному по уравнению

для каждого из участков трубопровода.
ν = 0,01 см2/с = 0,01/10000 =0,000001 м2/с.
Re1 = 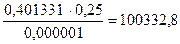
Re2 = 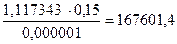
Re3 = 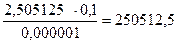
Reгр1 = 500 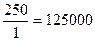
Reгр2 = 500 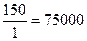
Reгр3 = 500 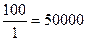
Полученные значения чисел Рейнольдса Re больше значений Reгр в последних двух случаях, это говорит о правильности предположения о наличии четвертой области сопротивления, расход жидкости определен верно.
Полученные значения чисел Рейнольдса Re меньше значений Reгр для первого случая, это говорит о неправильности предположения о наличии четвертой области сопротивления.
Для определения λ пер в этой области можно воспользоваться формулой А.Д. Альтшуля.
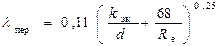
здесь 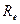 - число Рейнольдса, вычисленное по скорости, полученной по первому приближению для четвертой области сопротивления на соответствующем участке трубопровода.
- число Рейнольдса, вычисленное по скорости, полученной по первому приближению для четвертой области сопротивления на соответствующем участке трубопровода.
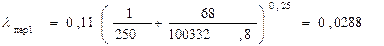
По формуле (2) рассчитываем скорость жидкости в трубах.
V1 = 0,40099 м/с
V2 = V1(S1/S2) =1,116392 м/с
V3 = V1(S1/S3) =2,502993 м/с
Определим расход жидкости по формуле Q = V1*S1 = 0,019648 м3/с.
б) Задвижка частично закрыта.
ξзадв = 400
Предполагаем во всех трубах IV зону сопротивления. При этом
 , kэк – абсолютная величина так называемой эквивалентной равномерно-зернистой шероховатости.
, kэк – абсолютная величина так называемой эквивалентной равномерно-зернистой шероховатости.
Так как трубы стальные, неновые, то kэк=1мм.

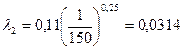
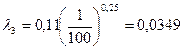
По формуле (2) рассчитываем скорость жидкости в первой трубе.
V1 = 0,268981 м/с.
V2 = V1(S1/S2) = 0,748868 м/с.
V3 = V1(S1/S3) =1,678991 м/с.
Определим расход жидкости по формуле Q = V1*S1 = 0,01318м3/с.
Выполним проверку правильности предположения о наличии четвертой области сопротивления на всех трех участках трубопровода. Для этого необходимо вычислить для каждого из участков числа Рейнольдса по уравнению
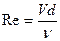
и сравнить полученные значения Re с граничным числом Рейнольдса, вычисленному по уравнению

для каждого из участков трубопровода.
ν = 0,01 см2/с = 0,01/10000 =0,000001 м2/с.
Re1 = 
Re2 = 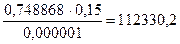
Re3 = 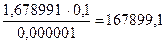
Reгр1 = 500 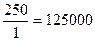
Reгр2 = 500 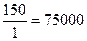
Reгр3 = 500 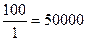
Полученные значения чисел Рейнольдса Re больше значений Reгр в последних двух случаях, это говорит о правильности предположения о наличии четвертой области сопротивления, расход жидкости определен верно.
Полученные значения чисел Рейнольдса Re меньше значений Reгр для первого случая, это говорит о неправильности предположения о наличии четвертой области сопротивления.
Для определения λ пер в этой области можно воспользоваться формулой А.Д. Альтшуля.
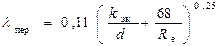
здесь 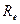 - число Рейнольдса, вычисленное по скорости, полученной по первому приближению для четвертой области сопротивления на соответствующем участке трубопровода.
- число Рейнольдса, вычисленное по скорости, полученной по первому приближению для четвертой области сопротивления на соответствующем участке трубопровода.
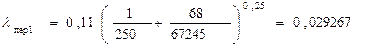
По формуле (2) рассчитываем скорость жидкости в трубах.
V1 = 0,268835 м/с
V2 = V1(S1/S2) =0,748462 м/с
V3 = V1(S1/S3) =1,678081 м/с
Определим расход жидкости по формуле Q = V1*S1 = 0,013173 м3/с.
| Величины | Значения величин | |
| При открытой задвижке | При прикрытой задвижке | |
| λ1 | 0,0288 | 0,02926 |
| λ2 | 0,0314 | 0,0314 |
| λ3 | 0,0349 | 0,0349 |
| ξзад | ||
| Q, м3/с | 0,019648 | 0,013173 |
| V1 м/с | 0,40099 | 0,268835 |
| V2 м/с | 1,116392 | 0,748462 |
| V3 м/с | 2,502993 | 1,678081 |
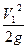 м м
| 0,008195 | 0,003684 |
 м м
| 0,063523 | 0,028552 |
 м м
| 0,319316 | 0,143525 |