Множества и операции над ними.
Понятие множества
Понятие множества является исходным строго не определяемым понятием. В математике понятие множество используется для описания совокупности объектов, отличающихся друг от друга и от объектов, не входящих в эту совокупность.
Примеры множеств: множество вершин данного многоугольника, множество натуральных чисел, множество студентов некоторой группы.
Множества обозначаются прописными буквами латинского алфавита:  ,
,  ,
,  , …, а входящие в них элементы – строчными:
, …, а входящие в них элементы – строчными:  ,
, 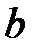 ,
,  , ….
, ….
Если элемент  принадлежит множеству
принадлежит множеству  , это обозначается
, это обозначается  , если не принадлежит -
, если не принадлежит -  .
.
Множество 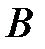 является подмножеством множества
является подмножеством множества  , если каждый элемент множества
, если каждый элемент множества  является элементом множества
является элементом множества  , обозначается:
, обозначается:  .
.
Символом  обозначается пустое множество, не содержащее ни одного элемента. Пустое множество является подмножеством любого множества.
обозначается пустое множество, не содержащее ни одного элемента. Пустое множество является подмножеством любого множества.
Множества называются равными, если они состоят из одних и тех же элементов, обозначается:  .
.
Обычно множества задаются одним из двух способов:
1. перечислением входящих в него элементов. Например: 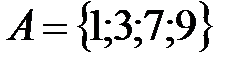 .
.
2. указанием характеристического свойства элементов множества, т.е. свойства, которым обладают все элементы множества и только они. Например:  - множество всех равнобедренных треугольников плоскости.
- множество всех равнобедренных треугольников плоскости.
Логические операции (связки)
Для сокращения записи высказываний, задающих множества, используют логическую символику.
Под высказыванием понимают языковое выражение, о котором можно судить истинно оно или ложно. Высказывания обозначаются прописными латинскими буквами:  ,
, 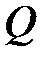 ,
,  , …. Каждому высказыванию можно приписать значение И (истина) или Л (ложь). Вместо этих символов будем применять числа 1 и 0 соответственно.
, …. Каждому высказыванию можно приписать значение И (истина) или Л (ложь). Вместо этих символов будем применять числа 1 и 0 соответственно.
Определим логические операции и проиллюстрируем их с помощью таблиц истинности:
· Дизъюнкция  (логическая сумма).
(логическая сумма).
Высказывание 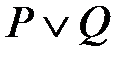 (читается: «
(читается: « или
или 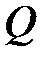 ») истинно тогда и только тогда, когда хотя бы одно из высказываний
») истинно тогда и только тогда, когда хотя бы одно из высказываний  или
или 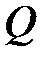 истинно.
истинно.
· Конъюнкция  (логическое умножение).
(логическое умножение).
Высказывание  (читается: «
(читается: « и
и 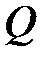 ») истинно тогда и только тогда, когда оба высказывания
») истинно тогда и только тогда, когда оба высказывания  и
и 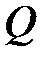 истинны.
истинны.
· Отрицание  (или
(или  ).
).
Высказывание  (читается: «не
(читается: «не  », «неверно, что
», «неверно, что  ») истинно тогда и только тогда, когда высказывание
») истинно тогда и только тогда, когда высказывание  ложно.
ложно.
· Импликация 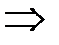 .
.
Высказывание 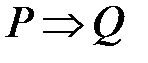 (читается: «из
(читается: «из  следует
следует 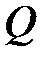 », «если
», «если  , то
, то 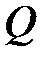 ») ложно тогда и только тогда, когда высказывание
») ложно тогда и только тогда, когда высказывание  истинно, а высказывание
истинно, а высказывание 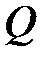 ложно.Во всех остальных случаях высказывание принимает истинное значение.
ложно.Во всех остальных случаях высказывание принимает истинное значение.
· Эквиваленция  .
.
Высказывание 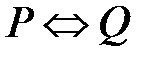 (читается: «
(читается: « тогда и только тогда, когда
тогда и только тогда, когда 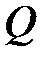 », «
», « эквивалентно
эквивалентно 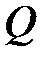 ») истинно тогда и только тогда, когда высказывания
») истинно тогда и только тогда, когда высказывания  и
и 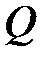 принимают одновременно одинаковые значения.
принимают одновременно одинаковые значения.
Таблицы истинности применяются для определения истинности или ложности высказывания.
Высказывания, не состоящие из каких-либо других высказываний, называются атомарными высказываниями. Атомарные высказывания также могут принимать одно из двух истинностных значений: истина или ложь. Символы, с помощью которых обозначают атомарные высказывания, называют атомами. Например, высказывание 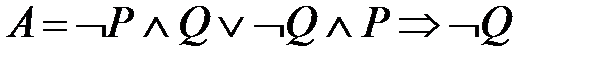 состоит из атомов
состоит из атомов 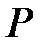 и
и  .
.
Очередность выполнения всех логических операций определяется расстановкой скобок. Например, высказывание  можно переписать в виде
можно переписать в виде 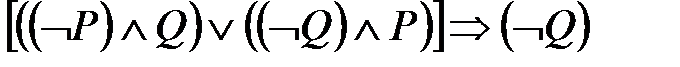 .
.
Порядок выполнения логических операций:
Пример: Составить таблицу истинности для высказывания 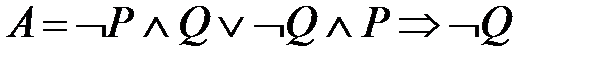 .
.
Решение:
Пример: При каких значениях атомов высказывание  принимает ложное значение?
принимает ложное значение?
Решение:
Рассмотрим множество всех высказываний. Введем на этом множестве операции сложения, умножения, дополнения, результаты которых также являются высказываниями. Тогда множество высказываний будет алгеброй, которую называют алгеброй высказываний или булевой алгеброй в честь английского математика Джорджа Буля.
Пример: Записать высказывания в виде формул, употребляя атомы для обозначения атомарных высказываний:
а) Если мистер Джонс счастлив, то миссис Джонс несчастлив, и если мистер Джонс несчастлив, то миссис Джонс счастлива.
Решение:
б) Или Сэм пойдет на встречу и Макс не пойдет, или Сэм не пойдет на встречу и Макс отлично проведет там время.
Решение: