Основные подходы к поиску оптимальных (рациональных) решений при Исследовании операций
Как уже говорилось ранее все задачи ИО можно условно разбить на две категории: прямые и обратные.
При решении прямых задач необходимо ответить на вопрос - “что будет, если в заданных условиях будет принято какое-то конкретное решение x*ÎX. То есть – чему будет равен выбранный показатель эффективности операции W(a,x*) (или ряд показателей при векторном критерии эффективности).
В общем случае решение таких задач достаточно просто. Для этого необходимо построить математическую модель операции, позволяющую определить один или несколько показателей эффективности W через заданные условия а и элементы решения x.
При решении обратных задач требуется ответить на вопрос – «какое необходимо выбрать решение xоптÎX (оптимальное или рациональное) для того, чтобы обеспечить при этом наилучшее значение показателя (ряда показателей) эффективности W(a,xопт).
В случае векторного критерия эффективности при решении обратной задачи под наилучшим (рациональным) обычно понимается решение, обеспечивающее:
- либо максимальное (минимальное) значение некоторого обобщенного (скалярного) показателя U, который представляет собой результат формализованной (неформализованной) свертки векторного критерия
мax U = U(W).
При этом основная проблема заключается в построении обобщенного показателя, отвечающего цели операции и учитывающего различный вклад частных показателей.
- либо решения (одно из решений), отвечающее условию, что нельзя найти другое решение, позволяющее улучшить любой из показателей Wi (i = 1,к), не ухудшая при этом значения других показателей Wx (x¹i) (хотя бы одного из них). Такие решения называются эффективными или Паретовскими (x п ÎX п ).
Если множество всех возможных решений конечно, топоиск эффективных (Паретовских) решений xпÎXп может быть осуществлен путем прямого перебора всех возможных решений xÎX со сравнением соответствующих значений компонент векторного критерия W(x).
Следует подчеркнуть, что выбор наилучшего решения среди множества найденных Паретовских xÎXп производится ЛПР.
В общем случае, задача поиска рационального решения даже при векторном критерии эффективности также сводится к необходимости решения задачи (или совокупности задач) математического программирования.
Остановимся несколько подробнее на их постановке и методах решения.
Под задачами математического программирования (планирования) понимается задачи поиска (планирования) наилучших управлений, возникающие в связи с необходимостью повышения эффективности функционирования некоторой системы (промышленной, транспортной, военной) за счет поиска наилучшего управления работой системы.
Задача мат. программирования в общем случае сводится к следующей. Найти значения переменных x1,…xn, доставляющие максимум (минимум) заданной скалярной функции
f(x1,…xn; a)
При условиях
gi (x1,…xn) ≤ (≥, =) bi, где i=1,…,m.
Здесь a и bi – константы, определяемые из физических условий задачи.
Условия gi(x1,…xn) ограничивают возможность выбора значений переменных x1,…xn из множества всех возможных значений. Множество точек Х= { x1,…xn }, удовлетворяющих системе ограничений gi (i=1,…,m) есть область определения X в поставленной задаче.
Функция f(x1,…xn; a) называется целевой функцией, которая может достигать экстремальных значений в одной или нескольких точках области X, которые предстоит найти (в конкретных задачах ИО в качестве целевой функции используют критерий эффективности, вычисляемый на основе модели операции).
Обычно вид функций f и g известен, константы ͞ a и bi, вытекающие из параметров исследуемой системы и целей, стоящие перед ней – заданы, число переменных n и ограничений m – определено. Кроме того, при необходимости, специально оговариваются ограничения на не отрицательность и целочисленность переменных xi (i=1,…,n) исходя из их физической природы, которые также входят в систему ограничений на переменные.
Исходя из вышесказанного формальная запись задачи математического программирования имеет вид:
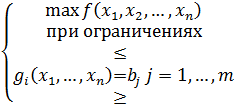
Параметр a входит в вид самой целевой функции и в дальнейшем может быть опущен.
В зависимости от вида целевой функции и ограничений можно выделить следующие классы задач:
1. Задачи линейного программирования. В них целевая функция и ограничения линейны относительно переменных xi (наиболее изученный класс задач).
2. Задачи нелинейного программирования. Сюда относятся задачи, в которых целевая функция или ограничена, либо и то и другое вместе – нелинейные функции. Среди них задачи с целевой функцией, представленной в виде суммы произвольных функций отдельных переменных xi (сепарабельной, аддитивной), с целевой функцией в виде полинома второй степени относительно xi (квадратической целевой функции) и т.д.
Особо выделяются задачи выпуклого программирования. Это такие задачи, когда целевая функция f и множество возможных решений X – выпуклые. Поиск оптимального решения в этом случае существенно упрощается.
Множество X называется выпуклым, если для любых двух точек x1,x2 Î X оно содержит в себе весь отрезок, их соединяющий:

Функция f(x) называется выпуклой (выпуклой вниз) на интервале [x1,x2], если для любой точки  (
(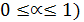 внутри этого интервала выполняется условие f(
внутри этого интервала выполняется условие f( ) ≤
) ≤  .
.
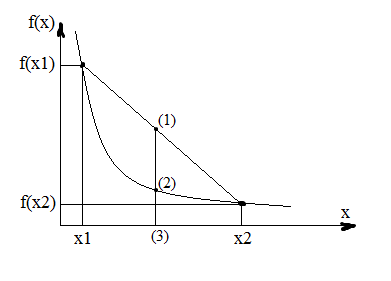
Здесь
 - точка (1);
- точка (1);
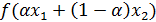 - точка (2);
- точка (2);
 - точка (3).
- точка (3).
То есть в любой промежуточной точке (3) значение функции (2) не превосходит значение показателя на прямой, соединяющей границы области (1).
Если f(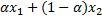 ) ≥
) ≥  , то функция называется вогнутой или выпуклой вверх.
, то функция называется вогнутой или выпуклой вверх.
Выпуклость целевой функции и ограничений позволяют формулировать и использовать условия существования оптимальных решений (экстремума) вне зависимости от их конкретного вида и формы задания.
К случае, если выпуклость целей функции области X нарушается, возможно существование множества точек xÎX, в которых достигается экстремум целевой функции, что значительно усложняет задачу поиска оптимального решения (задачи невыпуклого программирования).
По ограничениям, накладываемым на переменные xi можно выделить задачи с непрерывными и дискретными переменными. Дискретность переменных нарушает выпуклость множества X и приводит, как правило, к необходимости либо полного, либо направленного перебора всех возможных решений xÎX, что значительно увеличивает трудоемкость решения задачи.
Следует отметить, что приведенная классификация задач математического программирования достаточно условна и конкретные задачи могут содержать в себе сразу ряд признаков. Например, задача нелинейного, выпуклого программирования и т.п.
Рассмотрим более подробно ряд традиционных задач математического программирования и методов их решения.
Задачи линейного программирования (ЗЛП)
ЗЛП – задача математического программирования с линейной целевой функцией и линейными ограничениями. Является наиболее изученной задачей мат. программирования. Обычно на практике возникает при решении задач, связанных с распределением ресурсов, планированием производства, организацией работы транспорта и т.п., так как в этих случаях “расходы” и “доходы”,как правило линейно (или близко к линейным) связаны с количеством затраченных средств. (Например стоимость партии товаров линейно зависит от их количества, оплата перевозок пропорциональна весу перевезенных грузов (или расстоянию и весу) и т.п.
В общей постановке ЗЛП состоит в отыскании значений n переменных  ,
, 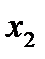 ,…,
,…, 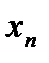 , доставляющих экстремум целевой функции вида
, доставляющих экстремум целевой функции вида
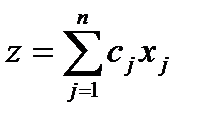
при ограничениях

и 

Система ограничений задает область допустимых решений X. В общем случае она представляет собой выпуклый многогранник в n -мерном пространстве. Вершины его являются крайними точками и их число конечно.
В математике доказано, что решение ЗЛП, если оно существует, всегда достигается хотя бы в одной крайней точке указанного многогранника.
На этом свойстве ЗЛП построены все методы её решения. Суть их заключается в организации перебора крайних точек таким образом, чтобы значение целевой функции при движении от точки к точке не уменьшалось.
Это обеспечивает поиск решения за ограниченное число шагов, исключая полный перебор всех крайних точек. Например Симплекс-метод.
Существуют стандартные программы, реализующие методы решения ЗЛП.
(Лит-ра: Вагнер Г.,Основы исследования операций,М.Мир,1972, т.1;
Таха Х., Введение в исследование операций, М.Мир,1985,т.1).
Пример:
Предприятие производит выпуск изделий двух наименований U  и U
и U  .
.
На изготовление изделий необходимо сырье 3-х видов - S  , S
, S 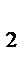 , S
, S  , причем на изготовление единицы продукции 1-го вида необходимо, соответственно, a
, причем на изготовление единицы продукции 1-го вида необходимо, соответственно, a  =1, a
=1, a  =2, a
=2, a 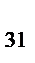 =2 единиц сырья, а на изготовление единицы продукции 2-го вида соответственно a
=2 единиц сырья, а на изготовление единицы продукции 2-го вида соответственно a  =1, a
=1, a  =5, a
=5, a 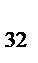 =2 единиц сырья.
=2 единиц сырья.
Реализация одного изделия 1-го вида приносит предприятию прибыль c  =3 ед., а 2-го вида - c
=3 ед., а 2-го вида - c 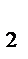 =4 ед.
=4 ед.
Необходимо так спланировать производство, т.е. определить объем выпуска изделий каждого вида, чтобы в рамках имеющихся ресурсов каждого вида b  =8 ед., b
=8 ед., b 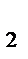 =30 ед., b
=30 ед., b  =14 ед., обеспечить максимальную прибыль (доход).
=14 ед., обеспечить максимальную прибыль (доход).
Обозначим  и
и 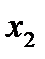 - объем выпускаемой продукции вида U
- объем выпускаемой продукции вида U  и U
и U  . Тогда формально задачу можно записать следующим образом:
. Тогда формально задачу можно записать следующим образом:
 (
(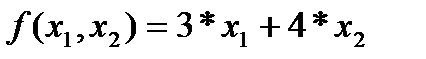 )
)
при ограничениях на ресурсы:
a 
 + a
+ a 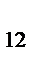
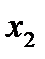
 b
b  (
( +
+ 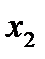
 8)
8)
a 
 + a
+ a 
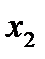
 b
b  (2
(2  +5
+5 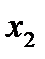
 30)
30)
a 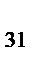
 + a
+ a 
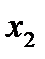
 b
b  (2
(2  +
+ 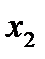
 14)
14)
и на переменные 
 0,
0, 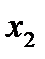
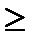 0;
0;
Как видим в нашем случае целевая функция и ограничения линейны, т.е. мы получим ЗЛП.
Для случаев 2-х переменных ЗЛП удобно решать графически. Так для рассмотренного выше примера при заданных значениях параметров получим:
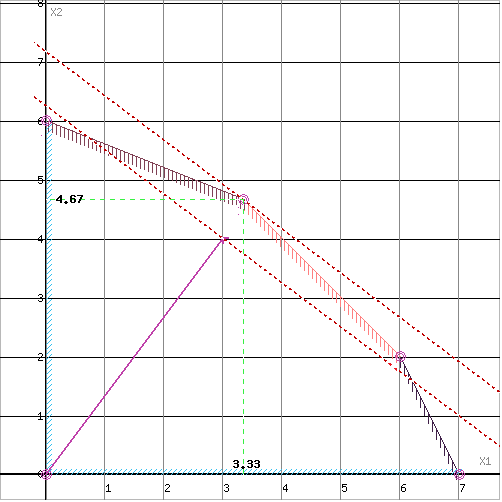
Выделим допустимую область решения и построим градиент целевой функции 
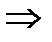 max.
max.

При ограничениях:
 +
+ 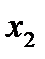
 8 (1)
8 (1)
2  +5
+5 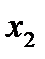
 30 (2)
30 (2)
2  +
+ 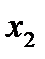
 14 (3)
14 (3)
 ,
, 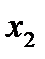
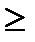 0
0
Оптимальное решение достигается в точке:
 =
= 
 =
= 
Значение целевой функции (полученная прибыль) 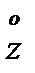 =
= 
Найденное оптимальное решение в общем случае может быть нецелочисленным. Однако в ряде задач это может быть неприемлемо из-за физической его не реализуемости.
В этом случае наряду с ограничениями не отрицательности переменных вводятся требования по их целочисленности, что значительно повышает сложность решения задачи, т.к. простое округление полученного решения до ближайших целых, как правило, не позволяет получить оптимального решения и, кроме того, может вывести его из области допустимых. Округление допустимо лишь в тех случаях, когда это не выводит из области допустимых решений и изменение целевой функции при отклонении решения от строго оптимального – не значительно.