Основные теоретические положения. ИССЛЕДОВАНИЕ ЧАСТОТНО УПРАВЛЯЕМОГО ЭЛЕКТРОПРИВОДА С АВТОНОМНЫМ ИНВЕРТОРОМ

Лабораторная работа №2

 

ИССЛЕДОВАНИЕ ЧАСТОТНО УПРАВЛЯЕМОГО ЭЛЕКТРОПРИВОДА С АВТОНОМНЫМ ИНВЕРТОРОМ

 

Цели работы:

1. Экспериментальное снятие механических характеристик при изменении частоты и напряжения статора одновременно.

2. Определение момента инерции привода с асинхронным двигателем методом свободного выбега.

 

 

Основные теоретические положения

 

Скорость вращения асинхронного двигателя (АД) может регулироваться изменением частоты питающего напряжения, что вытекает из формулы:

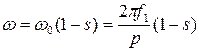, (1)

 

где ω₀ - синхронная скорость двигателя;

f ₁ - частота напряжения статора;

р - число пар полюсов двигателя;

s - скольжение двигателя.

Для получения регулируемой частоты в электроприводах применяются статические преобразователи частоты, построенные на базе тиристоров.

Критическое скольжение АД обратно пропорционально частоте:

 

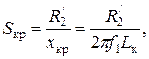(2)

 

L _к - индуктивность короткого замыкания.

Если при номинальной частоте f ₁ критическое скольжение равно S _КР, то при f ₁^/, отличной отноминальной:

 

. (3)

Так как ω₀ и х_к пропорциональны частоте, то критический момент АД обратно пропорционален квадрату частоты:

 

. (4)

При постоянном значении М₁ формулу (4) можно записать в виде:

 

, (5)

где 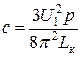- постоянная величина.

Если при номинальной частоте f₁ критический момент равен М_кр, то при частоте f₁^/:

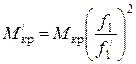. (6)

Поэтому при неизменном напряжении с увеличением частоты критический момент резко падает (рис. 1.а). Если учесть сопротивление обмотки статора, то критический момент будет изменяться не обратно пропорциональна квадрату частоты, а в несколько меньшей степени.

Из рис. 1, а видно, что при регулировании частоты тока статора АД и неизменной величине подводимого напряжения механические характеристики имеют неплохой вид, так как они отличаются высокой жесткостью. Однако при низких частотах, когда индуктивное сопротивление обмоток статора мало, происходит существенное возрастание тока и недопустимый перегрев двигателя. В связи с этим регулирование в широком диапазоне скорости АД изменением только частоты тока статора на практике не применяется.

Скорость вращения асинхронного двигателя в ограниченном диапазоне может регулироваться и изменением подводимого к нему напряжения при постоянной частоте тока статора. При этом момент, развиваемый двигателем, пропорционален квадрату приложенного напряжения:

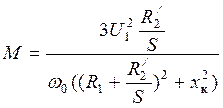, (7)

 

а ток двигателя – напряжению.

 

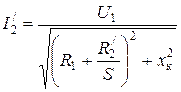, (8)

 

где .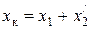

 

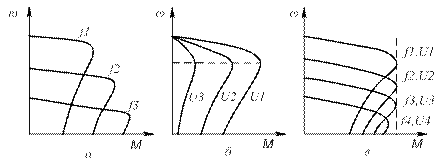
Рис.1. Механические характеристики асинхронного двигателя при регулировании скорости вращения: а – частотой (f1 > f2 >f3, U1=const); б -напряжением (U₁ > U₂ > U₃, f₁=const); в - частотой и напряжением при U/f=const.

 

Эти выражения дают возможности построить характеристики двигателя при напряжении статора, отличном от номинального (pис.1,б). Из семейства характеристик видно, что критическое скольжение для всех характеристик остается неизменным. Оно не зависит от приложенного напряжения. Крутизна характеристик возрастает при пониженном напряжении. Устойчивая работа АД при постоянном статическом моменте возможна только в интервале отсинхронной скорости до S_к.

Критический момент АД при снижении напряжения статора U1 уменьшается в соответствии с выражением (4).

Из рис.1.бвидно, что при уменьшении напряжения на АД необходимо одновременно снизить величину нагрузки на валу двигателя. В противном случае при неизменной нагрузке токв обмотке ротора возрастает, что приводит к перегреву этой обмотки, сопровождающемуся повышенным износом ее изоляции. При частых перегрузках возможен перегрев стержней обмотки ротора и даже их выплавление.

Таким образом, оба вышеуказанных варианта регулирования скорости АД имеют существенные недостатки, от которых избавиться можно только в случае поддержания критического момента двигателя постоянным. Для этого необходимо согласно выражению (4) одновременно изменять напряжение ичастоту тока статора.

Для асинхронного двигателя можно приближенно принять, что 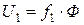. Поэтому для сохранения постоянства магнитного потока необходимо производить регулирование с неизменным соотношением:

 

.

Механические характеристики АД при таком способе регулирования скорости имеют вид, показанный на рис1,в. Жесткость харак­теристик в рабочей зоне сохраняется достаточно высокой. Величина критического момента в зоне больших частот сравнительно мало из­меняется. Лишь при низких частотах вследствие относительного увеличения падения напряжения в статоре происходит заметное уменьшение магнитного потока, а следовательно, и уменьшение критического момента. Это подтверждается анализом формулы:

 

. (9)

Для больших частот величина R₁ значительно меньше х_к, поэтому ею можно пренебречь, а формула (9) примет вид (4).

Так как 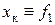и , то:

 

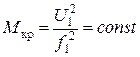. (10)

При значительном снижении частоты эти соотношения нарушаются, так как реактивное сопротивление рассеяния х_к = х₁ + х₁^/ста­новится сравнимым по величине с сопротивлением статора R₁илидаже меньше его. Влияние падения напряжения в статоре сказывается сильнее, и это приводит к уменьшению критического момента.

Для поддержания достаточной перегрузочной способности двигателя желательно, чтобы при малых частотах напряжение уменьшалось в меньшей степени, чем частота.

Учитывая вышеизложенное следует отметить, что в электроприводе переменного тока перспективным способом регулирования скорости вращения двигателей в широких пределах при частых пусках и торможениях является частотный способ с одновременным регулированием напряжения и частоты тока статора, так как он позволяет получить от простого и надежного асинхронного двигателя с короткозамкнутым ротором все необходимые для технологий производства механические характеристики, в том числе высокие частоты вращения при небольших потерях электроэнергии на тиристорном преобразователе.

Расчет механических характеристик АД при изменении параметров питающей сети, т.е. напряжения и частоты, может быть выполнен по выражению

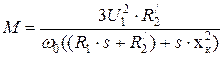, (11)

где ω₀ = 2πf₁ - синхронная скорость;

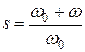- скольжение.

Момент инерции привода, его маховый момент и электромеханическая постоянная времени могут быть определены в результате проведения опыта свободного выбега привода.

Сущность свободного выбега или самоторможения заключается в следующем. Если отключить от сети асинхронный работающий вхолостую, то ротор двигателя и соединенная с ним рабочая машина, будут продолжать вращаться за счет запаса кинетической энергии, постепенно замедляясь из-за действия тормозящих сил, обусловленных потерями вращения (рис. 2).

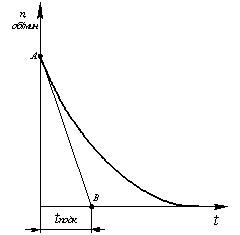Определение момента инерции асинхронного двигателя, соединенного с рабочей машиной (или без нее), производится при помощи касательной, проводимой в начальной точке А (см.рис.2) к кривой n = f(t). Этот метод является приближенным.

Основное уравнение движения электропривода имеет следующий вид:

 

, (12)

Рис. 2. Зависимость n=f(t), снимаемая в результате опыта свободного выбега.

 

где	МД	-	момент двигателя, Н·м;
МС	-	момент сопротивления, Н·м;
n	-	скорость, об/мин;
t	-	время, с;
J	-	Момент инерции.

 

 

В случае самоторможения М_Д = 0, а М_С является общим моментом сопротивления механизма и моментом потерь вращения привода, поэтому выражение (12) для J примет вид:

 

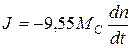. (13)

Если снята кривая выбега (см. рис.2), то проводя касательную к этой кривой в начальной точке выбега Адо пересечения с осью абсцисс, получают величину подкасательной t _подк. Изполученно­го треугольника ОАВвидно, что

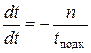. (14)

Тогда

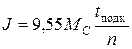. (15)

Величина момента сопротивления определяется но формуле

 

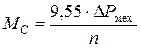. (16)

где ΔР _мех - механические потери вращения привода, соответствующие скорости n, Вт.

Механические потери вращения находятся из потерь холостого хода Р₀, которые в свою очередь состоят из потерь в стали статора, механических потерь вращения и потерь в меди статора. Потери в меди статора (Вт) определяются по формуле:

 

, (17)

 

где	I1	-	линейный ток статора, А;
	Rст	-	сопротивление фазы статора, Ом.

 

Суммарные потери в стали статора и механические потери вращения находят следующим образом:

 

. (18)

 

Для того, чтобы найти , необходимо отделить от Р _ст.мех потери встали статора. Это достигается построением зависимости 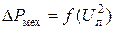(рис.3.) по нескольким точкам. Экстраполируя кривую до оси ординат, получают значение , так как при U_л=0 потери в стали статора равны нулю, и, следовательно, остаются одни механические потери вращения.

 

Рис.3. Зависимость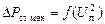

В теории электропривода часто оперируют не моментами инерции, а маховыми моментами, обозначаемыми (Нм²):

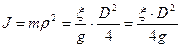, (19)

где	m	-	масса вращающихся частей, кг;
	ρ	-	радиус инерции, м;
	ξ	-	вес вращающихся частей, Н;
	g	-	ускорение свободного падения
	D	-	диаметр инерции, м.

 

Отсюда находим:

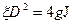. (20)

Зная момент инерции, можно также определить электромеханическую постоянную времени привода, под которой понимается время, в течение которого привод, обладающий моментом инерции J, разгоняется без нагрузки из неподвижного состояния до скорости идеального холостого хода ω₀ при неизменном моменте, равном момен­ту короткого замыкания М_К:

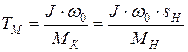, (21)

где s _н - номинальное скольжение, ;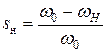

М_Н - номинальный момент двигателя, .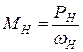

Величина электромеханической постоянной времени зависит от сопротивления цепи статора и не зависит от нагрузки привода.