Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«Российский экономический университет имени Г.В. Плеханова»
Волгоградский филиал
Кафедра социально-гуманитарных и математических дисциплин
Задания и методические рекомендации по выполнению контрольной работы
Часть 1
Наименование дисциплины Эконометрика
Рекомендуется для направления подготовки 080100 Экономика, 080200 Менеджмент
Профили: «Финансы и кредит», «Экономика предприятий и организаций»,
«Бухгалтерский учет, анализ и аудит», «Менеджмент организации торговли», «Экономика и управление организацией», «Менеджмент на предприятиях ресторанно-гостиничного бизнеса»
Квалификация (степень) выпускника: бакалавр
Форма обучения заочная
Разработчик:
доцент кафедры социально-гуманитарных и математических дисциплин
Шаркевич И.В.
Волгоград 2015
Методические рекомендации по выполнению контрольных работ
Вариант контрольной работы студент выбирает самостоятельно, в соответствии с последней цифрой зачетной книжки (если последняя цифра 0, необходимо выбрать вариант № 10). На титульном листе должен быть обязательно указан шифр зачетной книжки и номер варианта.
Контрольная работа, выполненная не по своему варианту, возвращается студенту без проверки.
Задание на выполнение контрольной состоит из 4 задач для каждого варианта по следующим темам:
Часть 1. Парная регрессия;
1) линейная парная регрессия;
2) нелинейная парная регрессия.
Часть 2. Множественная регрессия и моделирование временных рядов
3) множественная линейная парная регрессия;
4) моделирование временных рядов.
Выполненная контрольная работа должна быть зарегистрирована в деканате заочного обучения и дополнительного образования и сдана преподавателю на консультации перед экзаменом.
При выполнении контрольной работы надо соблюдать следующие правила:
1. указывать вариант контрольной работы;
2. расчеты производить с помощью компьютерных пакетов (Excel, Statistica, SPSS, и др. по выбору студента);
3. представлять решения задач подробно, со всеми формулами, расчетами и пояснениями.
4. проверять правильность примененных методов решения задач;
5. формулировать четкие, грамотные, обоснованные выводы;
6. в конце контрольной работы необходимо привести перечень использованной литературы и поставить свою личную подпись.
Контрольная работа, выполненная не по своему варианту, не зачитывается.
Страницы контрольной работы должны быть пронумерованы и иметь поля для замечаний преподавателя. В конце работы должен быть представлен список использованной литературы, ставится дата и подпись студента.
Выполненная контрольная работа представляется в университет для рецензирования. Правильно выполненная работа зачитывается. Если по зачтенной работе рецензентом будут сделаны замечания, необходимо разобраться в них, внести требуемые исправления и представить соответствующие доработки преподавателю.
Студенты, не получившие зачет по контрольной работе, к сдаче экзамена не допускаются. На экзамене студенты должны быть готовы ответить на вопросы преподавателя по решению задач контрольной работы.
Часть 1
Контрольные задания № 1
МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Пример 1. По территориям региона приводятся данные за 199X г.
(таб. 1.1).
Таблица 1.1
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., x | Среднедневная заработная плата, руб., y |
Задания:
1. Рассчитать линейный коэффициент парной корреляции, оценить его статистическую значимость и построить для него доверительный интервал с уровнем значимости a=0,05.
2. Построить линейное уравнение парной регрессии y на x и оценить статистическую значимость параметров регрессии. Сделать рисунок.
3. Оценить качество уравнения регрессии при помощи коэффициента детерминации. Проверить качество уравнения регрессии при помощи F -критерия Фишера.
4. Выполнить прогноз заработной платы y при прогнозном значении среднедушевого прожиточного минимума x, составляющем 107% от среднего уровня. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал для уровня значимости a=0,05.
Решение
1. Для определения степени тесноты связи обычно используют линейный коэффициент корреляции:
,
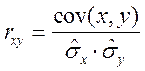где 
, 
– выборочные дисперсии переменных x и y, 
– ковариация признаков. Соответствующие средние определяются по формулам:
 ,
|  ,
|
 ,
|  .
|
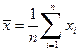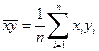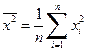Для расчета коэффициента корреляции (1.1) строим расчетную таблицу (табл. 1.2):
Таблица 1.2
| x | y | xy | x2 | y2 |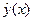 
| 
| e2 | |
| 148,77 | -15,77 | 248,70 | ||||||
| 152,45 | -4,45 | 19,82 | ||||||
| 157,05 | -23,05 | 531,48 | ||||||
| 149,69 | 4,31 | 18,57 | ||||||
| 158,89 | 3,11 | 9,64 | ||||||
| 174,54 | 20,46 | 418,52 | ||||||
| 138,65 | 0,35 | 0,13 | ||||||
| 157,97 | 0,03 | 0,00 | ||||||
| 144,17 | 7,83 | 61,34 | ||||||
| 157,05 | 4,95 | 24,46 | ||||||
| 146,93 | 12,07 | 145,70 | ||||||
| 182,83 | -9,83 | 96,55 | ||||||
| Итого | 1574,92 | |||||||
| Среднее значение | 85,58 | 155,75 | 13484,00 | 7492,25 | 24531,42 |
По данным таблицы находим:
, 
,
, 
,
, 
,
, 
,
,. 
.
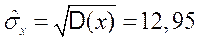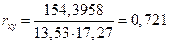Таким образом, между заработной платой (y) и среднедушевым прожиточным минимумом (x) существует прямая достаточно сильная корреляционная зависимость.
Для оценки статистической значимости коэффициента корреляции рассчитывают двухсторонний t-критерий Стьюдента:
,
который имеет распределение Стьюдента с k = n –2 и уровнем значимости a.
В нашем случае
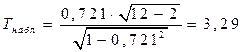и 
.
Поскольку 
, то коэффициент корреляции существенно отличается от нуля.
Для значимого коэффициента можно построить доверительный интервал, который с заданной вероятностью содержит неизвестный генеральный коэффициент корреляции. Для построения интервальной оценки (для малых выборок n <30), используют z-преобразование Фишера:
Распределение z уже при небольших n является приближенным нормальным распределением с математическим ожиданием 
и дисперсией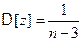 
. Поэтому вначале строят доверительный интервал для M[ z ], а затем делают обратное
z -преобразование.
Применяя z -преобразование для найденного коэффициента корреляции, получим
.
Доверительный интервал для M(z) будет иметь вид
,
где t g находится с помощью функции Лапласа F(t g)=g/2. Для g=0,95 имеем t g=1,96. Тогда
,
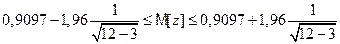или
.
Обратное z -преобразование осуществляется по формуле
В результате находим
.
В указанных границах на уровне значимости 0,05 (с надежностью 0,95) заключен генеральный коэффициент корреляции r.
2. Таким образом, между переменными x и y имеет существенная корреляционная зависимость. Будем считать, что эта зависимость является линейной. Модель парной линейной регрессии имеет вид
Пропускаем!!!!!!!
,
где y – зависимая переменная (результативный признак), x – независимая (объясняющая) переменная, e – случайные отклонения, b0 и b1 – параметры регрессии. По выборке ограниченного объема можно построить эмпирическое уравнение регрессии:
,
где b0 и b1 – эмпирические коэффициенты регрессии. Для оценки параметров регрессии обычно используют метод наименьших квадратов (МНК). В соответствие с МНК, сумма квадратов отклонений фактических значений зависимой переменной y от теоретических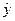 
была минимальной:
,
где 
– отклонения yi от оцененной линии регрессии. Необходимым условием существования минимума функции двух переменных (1.12) является равенство нулю ее частных производных по неизвестным параметрам b0 и b1. В результате получаем систему нормальных уравнений:
Решая систему (1.13), найдем
,
.
По данным таблицы (1.2) находим
;
.
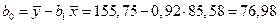Получено уравнение регрессии:
.
Параметр b 1 называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. В рассматриваемом случае, с увеличением среднедушевого минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
Рис. 1.1
Проверка адекватности моделей, построенных на основе уравнений регрессии, начинается с проверки статистической значимости каждого коэффициента регрессии. Для этого вычислим сначала стандартную ошибку регрессии
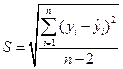. (1.17)
В нашем случае
.
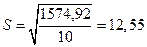Значимость коэффициентов регрессии осуществляется с помощью t-критерия Стьюдента:
, (1.18)
где 
– стандартная ошибка коэффициента регрессии.
Для коэффициента b 1 оценку дисперсии можно получить по формуле:
. (1.19)
В нашем случае
Следовательно,
.
Отметим, что для парной линейной регрессии t -критерий для коэффициента корреляции rxy и коэффициента регрессии b 1 совпадают.
Для коэффициента b 0 оценку дисперсии можно получить по формуле:
. (1.20)
Тогда
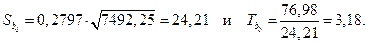
Критическое значение критерия было уже найдено 
. Поскольку 
и 
, то коэффициенты регрессии значимо отличаются от нуля. Следовательно, для них можно построить доверительные интервалы.
Определим предельные ошибки для каждого показателя:
, 
,
где 
. В нашем случае
, 
.
В результате, получаем следующие доверительные интервалы для коэффициентов регрессии:
и 
,
или
и 
.
Замечание. Задачи регрессионного анализа можно решать с использованием компьютеров. Например, можно использовать программу Excel. Для этого достаточно ввести свои данные и использовать пакет Анализ данных. Опишем кратко последовательность действий:
1) Проверьте доступ к пакету анализа. В главном меню последовательно выберите Сервис / Надстройки. Установите флажок Пакет анализа.
2) В главном меню выберите Данные / Анализ данных / Регрессия. Щелкните по кнопке ОК.
3) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон столбцов, содержащие значения факторов независимых признаков.
Результаты регрессионного анализа представлены в таблице 1.3.
Отметим, что в компьютерных программах вычисляется не критическое значение критерия, допустим Tкрит, а вероятность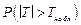 
. Если P <a, то нет оснований отклонять нулевую гипотезу, если P >a, то нулевая гипотеза отклоняется.
Таблица 1.3
| ВЫВОД ИТОГОВ | |||||||
| Регрессионная статистика | |||||||
| Множественный R | 0,721025214 | ||||||
| R-квадрат | 0,519877359 | ||||||
| Нормированный R-квадрат | 0,471865095 | ||||||
| Стандартная ошибка | 12,5495908 | ||||||
| Наблюдения | |||||||
| ДИСПЕРСИОННЫЙ АНАЛИЗ | |||||||
| df | SS | MS | F | Значимость F | |||
| Регрессия | 1705,327706 | 1705,327706 | 10,82801173 | 0,008141843 | |||
| Остаток | 1574,922294 | 157,4922294 | |||||
| Итого | 3280,25 | ||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | ||
| Y-пересечение | 76,9764852 | 24,21156138 | 3,179327594 | 0,0098300668 | 23,02975528 | 130,9232151 | |
| Переменная X 1 | 0,920430553 | 0,279715587 | 3,290594434 | 0,008141843 | 0,29718579 | 1,543675827 | |
3. Оценку качества построенной модели дает коэффициент детерминации.
Коэффициент детерминации для линейной модели равен квадрату коэффициента корреляции
Это означает, что 52% вариации заработной платы (y) объясняется вариацией фактора x – среднедушевого прожиточного минимума.
Значимость уравнения регрессии проверяется при помощи F -критерия Фишера, для линейной парной регрессии он будет иметь вид
, (1.21)
где F подчиняется распределению Фишера с уровнем значимости a и степенями свободы k 1=1 и k 2= n –2.
В нашем случае
.
Поскольку критическое значение критерия равно
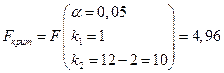
и 
, то признается статистическая значимость построенного уравнения регрессии. Отметим, что для линейной модели F - и t -критерии связаны равенством 
.
4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Прогнозное значение yp определяется путем подстановки в уравнение регрессии (1.16) соответствующего (прогнозного) значения xp. В нашем случае прогнозное значение прожиточного минимума составит: 
, тогда прогнозное значение прожиточного минимума составит:
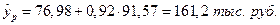
Средняя стандартная ошибка прогноза вычисляется по формуле:
. (1.22)
В нашем случае
Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:
.
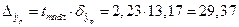Доверительный интервал прогноза
,
или
.
Выполненный прогноз среднемесячной заработной платы оказался надежным (g=0,95), но неточным, т.к. относительная точность прогноза составила 29,4/161,2×100%=18,2%.
МОДЕЛЬ ПАРНОЙ НЕЛИНЕЙНОЙ РЕГРЕССИИ
Пример 2. По имеющимся данным исследуется зависимость между темпом прироста заработной платы (x) и уровнем безработицы (y) (таб. 2.1).
Таблица 2.1
| Год | ||||||||||
| x | 1,61 | 1,66 | 1,80 | 1,95 | 2,05 | 2,12 | 2,25 | 2,45 | 2,55 | 2,67 |
| y | 1,0 | 1,38 | 1,15 | 1,50 | 1,55 | 1,20 | 1,10 | 1,0 | 1,35 | 1,8 |
| Год | ||||||||||
| x | 2,73 | 2,80 | 2,93 | 3,02 | 3,15 | 3,27 | 3,45 | 3,60 | 3,80 | |
| y | 1,90 | 1,45 | 1,85 | 1,20 | 1,50 | 1,25 | 1,40 | 1,30 | 1,60 |
Требуется:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи. Рассчитайте параметры уравнений степенной и обратной парной регрессии. Сделайте рисунки.
2. Дайте с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом. Оцените качество уравнения регрессии с помощью средней ошибки аппроксимации и коэффициента детерминации. Можно ли для оценки качества уравнения регрессии использовать критерий Фишера?
3. По значениям рассчитанных характеристик выберите лучшее уравнение регрессии. Дайте экономический смысл коэффициентов выбранного уравнения регрессии.
4. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости a=0,05.
Решение
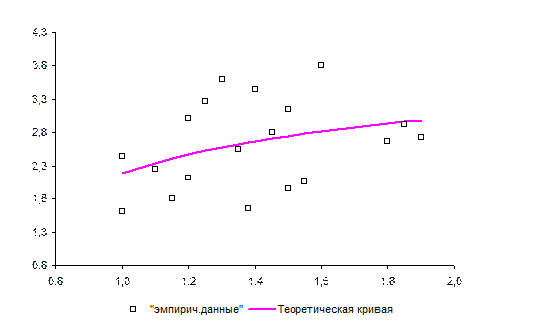
1. Построим поле корреляции (рис.2.1).
Рис. 2.1
По виду расположения точек можно предположить, что имеется слабая положительная корреляционная зависимость.
2а. Построению степенной модели
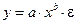
предшествует процедура линеаризации. В данном случае линеаризация производится путем логарифмирования обеих частей уравнения:
.
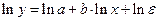По выборке ограниченного объема можно построить эмпирическое уравнение регрессии:
,
где 
Таким образом, степенная модель свелась к линейной модели с ее методами оценивания параметров и проверки гипотез (см. пример 1).
Для расчетов используем данные таблицы 2.2
Таблица 2.2
| u= ln x | v= ln y | uv | u2 | v2 | 
| 
| A | 
| 
| 
| |
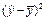
| 0,476 | 0,000 | 0,000 | 0,227 | 0,000 | 1,215 | -0,215 | 21,499 | 0,046 | 0,0319 | 0,155 | |
| 0,507 | 0,322 | 0,163 | 0,257 | 0,104 | 1,225 | 0,155 | 11,248 | 0,024 | 0,0285 | 0,000 | |
| 0,588 | 0,140 | 0,082 | 0,345 | 0,020 | 1,251 | -0,101 | 8,790 | 0,010 | 0,0203 | 0,059 | |
| 0,668 | 0,405 | 0,271 | 0,446 | 0,164 | 1,278 | 0,222 | 14,824 | 0,049 | 0,0135 | 0,011 | |
| 0,718 | 0,438 | 0,315 | 0,515 | 0,192 | 1,295 | 0,255 | 16,482 | 0,065 | 0,0098 | 0,024 | |
| 0,751 | 0,182 | 0,137 | 0,565 | 0,033 | 1,306 | -0,106 | 8,832 | 0,011 | 0,0077 | 0,038 | |
| 0,811 | 0,095 | 0,077 | 0,658 | 0,009 | 1,327 | -0,227 | 20,595 | 0,051 | 0,0045 | 0,086 | |
| 0,896 | 0,000 | 0,000 | 0,803 | 0,000 | 1,357 | -0,357 | 35,653 | 0,127 | 0,0014 | 0,155 | |
| 0,936 | 0,300 | 0,281 | 0,876 | 0,090 | 1,371 | -0,021 | 1,544 | 0,000 | 0,0005 | 0,002 | |
| 0,982 | 0,588 | 0,577 | 0,964 | 0,345 | 1,387 | 0,413 | 22,917 | 0,170 | 0,0000 | 0,165 | |
| 1,004 | 0,642 | 0,645 | 1,009 | 0,412 | 1,396 | 0,504 | 26,547 | 0,254 | 0,0000 | 0,256 | |
| 1,030 | 0,372 | 0,383 | 1,060 | 0,138 | 1,405 | 0,045 | 3,110 | 0,002 | 0,0001 | 0,003 | |
| 1,075 | 0,615 | 0,661 | 1,156 | 0,378 | 1,422 | 0,428 | 23,149 | 0,183 | 0,0008 | 0,208 | |
| 1,105 | 0,182 | 0,202 | 1,222 | 0,033 | 1,433 | -0,233 | 19,423 | 0,054 | 0,0016 | 0,038 | |
| 1,147 | 0,405 | 0,465 | 1,317 | 0,164 | 1,449 | 0,051 | 3,399 | 0,003 | 0,0031 | 0,011 | |
| 1,185 | 0,223 | 0,264 | 1,404 | 0,050 | 1,463 | -0,213 | 17,064 | 0,045 | 0,0048 | 0,021 | |
| 1,238 | 0,336 | 0,417 | 1,534 | 0,113 | 1,484 | -0,084 | 6,002 | 0,007 | 0,0082 | 0,000 | |
| 1,281 | 0,262 | 0,336 | 1,641 | 0,069 | 1,501 | -0,201 | 15,438 | 0,040 | 0,0115 | 0,009 | |
| 1,335 | 0,470 | 0,627 | 1,782 | 0,221 | 1,522 | 0,078 | 4,866 | 0,006 | 0,0165 | 0,043 | |
| Итого | 5,979 | 17,734 | 5,903 | 2,536 | 17,779 | 0,393 | 281,382 | 1,151 | 0,165 | 1,285 | |
| Среднее значение | 0,315 | 0,933 | 0,311 | 0,134 | 0,936 | 14,810 | 0,061 | 0,009 | 0,068 | ||
| s | 0,2541 | 0,0345 | |||||||||
| s 2 | 0,0646 | 0,2541 |
В соответствии с формулой (1.15) вычисляем
, 
.
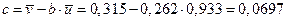В результате, получим линейное уравнение
.
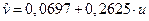Выполнив его потенцирование, находим искомое уравнение степенной:
.
Подставляя в данное уравнение фактические значения x, получаем теоретические значения
2б. Построению обратной модели
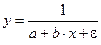
также предшествует процедура линеаризации путем преобразования 
. В результате получается линейное уравнение регрессии:
.
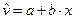Для расчетов используем данные таблицы 2.3
Таблица 2.3
| x | v= 1/ y | xv | x2 | v2 |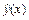 
| 
| A |
|
|
| |
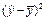
| 1,61 | 1,000 | 1,6100 | 2,592 | 0,048 | 1,220 | -0,220 | 21,956 | 0,048 | 0,030 | 0,155 | |
| 1,66 | 0,725 | 1,2029 | 2,756 | 0,024 | 1,225 | 0,155 | 11,213 | 0,024 | 0,028 | 0,000 | |
| 1,8 | 0,870 | 1,5652 | 3,240 | 0,008 | 1,242 | -0,092 | 7,957 | 0,008 | 0,023 | 0,059 | |
| 1,95 | 0,667 | 1,3000 | 3,803 | 0,058 | 1,259 | 0,241 | 16,041 | 0,058 | 0,018 | 0,011 | |
| 2,05 | 0,645 | 1,3226 | 4,203 | 0,078 | 1,272 | 0,278 | 17,961 | 0,078 | 0,015 | 0,024 | |
| 2,12 | 0,833 | 1,7667 | 4,494 | 0,006 | 1,280 | -0,080 | 6,691 | 0,006 | 0,013 | 0,038 | |
| 2,25 | 0,909 | 2,0455 | 5,063 | 0,039 | 1,297 | -0,197 | 17,886 | 0,039 | 0,009 | 0,086 | |
| 2,45 | 1,000 | 2,4500 | 6,003 | 0,104 | 1,323 | -0,323 | 32,292 | 0,104 | 0,005 | 0,155 | |
| 2,55 | 0,741 | 1,8889 | 6,503 | 0,000 | 1,336 | 0,014 | 1,007 | 0,000 | 0,003 | 0,002 | |
| 2,67 | 0,556 | 1,4833 | 7,129 | 0,200 | 1,353 | 0,447 | 24,836 | 0,200 | 0,002 | 0,165 | |
| 2,73 | 0,526 | 1,4368 | 7,453 | 0,290 | 1,361 | 0,539 | 28,349 | 0,290 | 0,001 | 0,256 | |
| 2,8 | 0,690 | 1,9310 | 7,840 | 0,006 | 1,371 | 0,079 | 5,425 | 0,006 | 0,000 | 0,003 | |
| 2,93 | 0,541 | 1,5838 | 8,585 | 0,211 | 1,390 | 0,460 | 24,852 | 0,211 | 0,000 | 0,208 | |
| 3,02 | 0,833 | 2,5167 | 9,120 | 0,041 | 1,404 | -0,204 | 16,970 | 0,041 | 0,000 | 0,038 | |
| 3,15 | 0,667 | 2,1000 | 9,923 | 0,006 | 1,423 | 0,077 | 5,104 | 0,006 | 0,001 | 0,011 | |
| 3,27 | 0,800 | 2,6160 | 10,693 | 0,037 | 1,442 | -0,192 | 15,378 | 0,037 | 0,002 | 0,021 | |
| 3,45 | 0,714 | 2,4643 | 11,903 | 0,005 | 1,471 | -0,071 | 5,097 | 0,005 | 0,006 | 0,000 | |
| 3,6 | 0,769 | 2,7692 | 12,960 | 0,039 | 1,497 | -0,197 | 15,119 | 0,039 | 0,011 | 0,009 | |
| 3,8 | 0,625 | 2,3750 | 14,440 | 0,005 | 1,532 | 0,068 | 4,281 | 0,005 | 0,019 | 0,043 | |
| Итого | 49,860 | 14,110 | 36,428 | 138,70 | 1,206 | 0,782 | 278,415 | 1,206 | 0,187 | 1,285 | |
| Среднее значение | 2,624 | 0,743 | 1,917 | 7,30 | 0,063 | 14,653 | 0,063 | 0,010 | 0,068 | ||
| s | 0,6430 | 0,1373 | |||||||||
| s 2 | 0,4135 | 0,0189 |
В соответствии с формулой (1.15) вычисляем
, 
.
В результате, получим уравнение обратной регрессии:
.
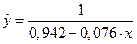Подставляя в данное уравнение фактические значения x, получаем теоретические значения результата 
.
2. Средний коэффициент эластичности
(2.7)
показывает, насколько процентов в среднем по совокупности изменится результат y от своей средней величины при изменении фактора x на 1% от своего среднего значения.
Для степенной функции 
. (2.8)
В нашем случае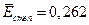 
.
Для обратной функции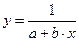 
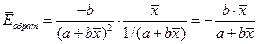. (2.9)
В нашем случае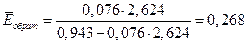 
.
Таким образом, при возрастании темпов роста заработной платы на 1% уровень безработицы возрастет на 0,27% (для обратной модели).
Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:
К/р зареги.
Конспект, на балл+
Вопрос 2 в билете.
Пятн-17-00
33-17-56.
. (2.10)
В нашем случае по данным таблиц 2.3 и 2.4 находим
.
| для степенной регрессии |  ,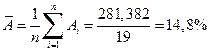
|
| для обратной регрессии |  .
|
Качество построенной модели оценивается как хорошее, если 
не превышает 8-10%. Поэтому рассмотренные модели "плохо" описывают имеющиеся статистические данные. Этот результат можно объяснить сравнительно небольшим числом наблюдений.
Коэффициент детерминации
(2.11)
характеризует долю дисперсии результативного признака, объясняемую регрессией, в общей дисперсии результативного признака. По данным таблиц 2.3 и 2.4 получаем
| для степенной регрессии |  ,
|
| для обратной регрессии |  .
|
Наибольшее значение коэффициент детерминации имеет для обратной модели (R 2=0,146). Однако он показывает, что уравнение регрессии только на 15% объясняет вариацию значений признака y.
Отметим, что в общем случае для нелинейных моделей критерий Фишера применять нельзя (почему?).
3. Из всех построенных уравнений регрессии наиболее оптимальными характеристиками обладает модель обратной регрессии:
. (2.13)
Оно имеет наименьшую ошибку аппроксимации (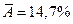
), и наибольший индекс детерминации (
), а также имеет наибольшую связь результативного признака с фактором (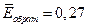
).
Для данного примера, кривая зависимости между темпом прироста заработной платы и уровнем безработицы называется кривой Филлипса. Если x =0, то получим естественный уровень безработицы
.
Таким образом, параметр 1/ a в обратной модели характеризует естественный уровень безра
4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Прогнозное значение yp определяется путем подстановки в уравнение регрессии (2.13) соответствующего (прогнозного) значения xp. В нашем случае прогнозное значение темпа прироста заработной платы равна x 0=4,0, тогда прогнозное значение уровня безработицы составит: