Форма поверхности Ферми определяет ряд свойств и важных характеристик металлов. Например, постоянная Холла в сильных полях в не скомпенсированных металлах в отсутствие открытых орбит при заданном направлении поля полностью определяется объемом k-пространства, заключенным внутри дырочной и электронной полостей поверхности Ферми. С формой поверхности Ферми тесно связаны кинетические коэффициенты металла, а также его равновесные и оптические свойства. Сопоставление с экспериментально определенной формой поверхности Ферми является критическим пунктом для оценки достоверности расчетов зонной структуры, базирующихся на тех или иных предположениях.
Основы некоторых из экспериментальных методов будут изложены в этой лекции. Основным методом исследования поверхности Ферми, с помощью которого получена большая часть информации, является метод, основанный на эффекте де Гааза - ван Альфена и на родственных ему эффектах.
 Рис.5.1. Осцилляции де Гааза- ван Альфена (dHvA) в серебре Рис.5.1. Осцилляции де Гааза- ван Альфена (dHvA) в серебре
|
28.Эффект де Гааза - ван Альфена(de Haas, van Alphen, 1930,1932 гг. Был предсказан Ландау(1930,1969). Заключается в осцилляциях магнитного момента, как функции напряженности магнитного поля. Эффект наблюдается в чистых образцах, при низких температурах и в сильных полях. Эффект заключается в осцилляциях намагниченности М как функции магнитного поля В. Примеры осцилляций dHvA приведены на рис. 5.1. Согласно теории Ландау, осцилляции могут быть объяснены как квантование замкнутых электронных орбит в магнитном поле. Для системы из N-электронов при абсолютном нуле уровни Ландау заполнены до магнитного квантового числа n = s, где s- целое число >0. Орбиты в следующем уровне n = s + 1 будут частично заполнены. Уровень Ферми будет располагаться на s+1, если он будет иметь хотя бы один электрон на нем. По мере увеличения магнитного поля В, электроны будут смещаться на более низкие уровни (поскольку вырождение (4.22) D =  B будет возрастать). При некотором критическом магнитном поле Вs нет ни одного частично заполненного уровня, уровень s+1 освобождается и уровень Ферми переходит на n=s, так что полное число электронов
B будет возрастать). При некотором критическом магнитном поле Вs нет ни одного частично заполненного уровня, уровень s+1 освобождается и уровень Ферми переходит на n=s, так что полное число электронов
sD = s  Bs = N Bs = N
| (5.1) |
Соответственно (4.24), полная энергия уровней, которые полностью заполнены
U1 =  sn=1D sn=1D  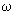 c (n-1/2) = 1/2 D c (n-1/2) = 1/2 D  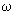 cs2 cs2
| (5.2) |
Полная энергия на электронов на частично занятом уровне s + 1 равна
U2 =  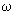 c (s+1/2)(N-sD) c (s+1/2)(N-sD)
| (5.3) |
Полная энергия
| U = U2 + U2 | (5.4) |
 Рис.5.2. Зависимость U(1/B) Рис.5.2. Зависимость U(1/B)
|
Зависимость U(1/B) схематично изображена на рис. 5.2. На этом рисунке нижняя кривая изображает энергию полностью заполненных уровней Ландау, U1, верхняя кривая - полную энергию, а затемненная часть отражает вклад частично заполненных состояний. Осцилляции энергии могут быть детектированы по осцилляциям магнитного момента
 = - = -  U/ U/  B B
| (5.5) |
Осцилляции μ(1/В) и есть эффект dHvA. Из (4.20) видно, что осцилляции проходят через равные интервалы в 1/В, так что инкремент составляет
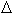 (1/B) = (2 (1/B) = (2  e/ e/  c) 1/Se, c) 1/Se,
| (5.6) |
где Se - согласно теории Онсагера, есть любая экстремальная замкнутая траектория, перпендикулярная В. Из измерений Δ(1/B) определяют соответствующую площадь Se, исходя из чего удается сконструировать форму и размеры поверхности Ферми.
 Рис.5.3. Дырочноподобные траектории электронов типа "собачьей кости" в благородных металлах Рис.5.3. Дырочноподобные траектории электронов типа "собачьей кости" в благородных металлах
|
Экстремальные орбиты. Реакция системы из N-электронов на магнитное поле исходит из вкладов всех сечений или всех орбит. Но в отклике будут доминировать те орбиты, которые являются равновесными, т.е. устойчивыми к малым отклонениям в k (мы имеем дело с пакетом Δ k). Такие орбиты называют экстремальными орбитами. Так при ориентации магнитного поля вдоль оси <111> кристаллов благородных металлов, например серебра как на рис. 5.2., выделяются два периода, один из которых соответствует движению по "пузу" поверхности Ферми (малое значение инкремента Δ(1/B)), другое - движению по "шейке" (большое Δ(1/B)). Эти траектории относятся к электронноподобному типу, поскольку охватывают заполненные состояния. Пример дырочноподобных электронных экстремальных орбит, типа "собачьей кости", приведен на рис.5.3. В этом случае траектория охватывает незаполненные состояния, соответственно, энергия состояний внутри контура выше, чем вне его. Этот пример показывает, что эффект dHvA выделяет достаточно сложные экстремальные орбиты.
Качественно выделение экстремальных орбит можно объяснить взаимным гашением фаз: вклады различных неэкстремальных орбит уничтожаются, однако, вблизи экстремумов фазы меняются медленно, фазы не гасятся полностью, и поэтому сигнал от этих орбит не исчезает.
Аналогичные (методу dHvA) методы. Среди других методов, аналогичных методу dHvA, следует, прежде всего отметить метод, базирующийся на эффекте Шубникова-де Гааза (1930), В этом методе наблюдаются осцилляции электрического сопротивления в магнитном поле.
Другие методы исследования поверхности Ферми. Дают менее однозначную геометрическую информацию по сравнению с эффектом dHvA, поэтому здесь приведено лишь очень краткая характеристика. Более полное изложение дано в АМ, Гл.14.
Магнитоакустический эффект. Исследуют затухание в металле звуковых волн, распространяющихся ^ -но приложенному постоянному магнитному полю В. Поскольку ионы, несущие акустическую волну, имеют заряд, то такая волна генерирует электрическое поле с теми же частотой, волновым вектором и поляризацией. Благодаря электромагнитной волне, электроны металла могут взаимодействовать со звуковой волной, усиливая или ослабляя ее. Если в промежутке между столкновениями электрон может совершать много оборотов в магнитном поле, т.е. 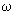 c
c  >>1, где
>>1, где  - среднее время между столкновениями, (сильное магнитное поле, низкие температуры, очень чистый монокристалл), то зависимость затухания звука от его длины от его длины волны имеет осцилляторный характер и может содержать информацию о поперечных (по отношению к В) сечениях поверхности Ферми. Осцилляции обусловлены условием резонанса в поглощении или усилении акустической волны, состоящим в кратности или полукратности отношения диаметра l c орбиты электрона вдоль распространения акустической волны (т.е.
- среднее время между столкновениями, (сильное магнитное поле, низкие температуры, очень чистый монокристалл), то зависимость затухания звука от его длины от его длины волны имеет осцилляторный характер и может содержать информацию о поперечных (по отношению к В) сечениях поверхности Ферми. Осцилляции обусловлены условием резонанса в поглощении или усилении акустической волны, состоящим в кратности или полукратности отношения диаметра l c орбиты электрона вдоль распространения акустической волны (т.е.  -но В) и длиной волны
-но В) и длиной волны  . Различают условие слабой связи (слабое поглощение/усиление) и сильной связи (сильное поглощение/усиление) электрона с волной:
. Различают условие слабой связи (слабое поглощение/усиление) и сильной связи (сильное поглощение/усиление) электрона с волной:
Слабая связь - l c = n 
| (5.7) |
Сильная связь - l c = (n+1/2) 
|
Нетрудно видеть, что в условиях слабой связи поглощение и усиление компенсируются в положительной и отрицательной полупериодах волны, чего не происходит в условиях сильной связи. Изменяя направление распространение звука и магнитного поля (с тем, чтобы могли проявиться различные экстремальные диаметры) иногда удается определить форму поверхности Ферми.
Аномальный скин-эффект.
Если металлический образец облучается микроволновым излучением с частотой 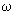 , не слишком высокой, то это излучение поглощается в слое толщиной
, не слишком высокой, то это излучение поглощается в слое толщиной  0, равной
0, равной
 0 = c/(2 0 = c/(2   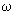 ), ),
| (5.8) |
где  - проводимость образца. Обычно
- проводимость образца. Обычно  0 >> l - длины свободного пробега при достаточно малой частоте
0 >> l - длины свободного пробега при достаточно малой частоте 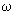 . Это т.н. "классическая" глубина скин-слоя. В случае
. Это т.н. "классическая" глубина скин-слоя. В случае  0 ~ l требуется более сложная теория, а режим
0 ~ l требуется более сложная теория, а режим  0 << l называют предельно аномальным. В предельно аномальном режиме неприменимо представление об экспоненциальном затухании поля с глубиной. Глубина проникновения и коэффициент отражения в этом случае определяются некоторыми характеристиками поверхности Ферми, которые зависят от ориентации этой поверхности относительно реальной поверхности кристалла.
0 << l называют предельно аномальным. В предельно аномальном режиме неприменимо представление об экспоненциальном затухании поля с глубиной. Глубина проникновения и коэффициент отражения в этом случае определяются некоторыми характеристиками поверхности Ферми, которые зависят от ориентации этой поверхности относительно реальной поверхности кристалла.