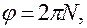Кинематика твердого тела

Плоское движение – это движение, при котором все точки твердого тела движутся в параллельных плоскостях.

Основными видами движения твердого тела являются: поступательное и вращательное. Остальные виды движения твердого тела можно свести к одному из основных движений либо к их совокупности.

Поступательное движение – это движение, при котором все точки твердого тела совершают за один и тот же промежуток времени одинаковые перемещения. При таком движении любая прямая, связанная с телом, все время остается параллельной самой себе.

Поскольку при поступательном движении все точки тела движутся одинаково, то задача описания движения твердого тела сводится к задаче кинематики материальной точки.

Простое вращательное движение (вращение вокруг неподвижной оси) – это движение, при котором все точки твердого тела движутся по концентрическим окружностям, центры которых лежат на оси вращения.

При простом вращательном движении угловые величины (перемещения, скорости, ускорения) всех точек тела одинаковы, а линейные – различны и зависят от расстояния точки до оси вращения.

Рассмотрим вращение твердого тела вокруг неподвижной оси.

Поскольку твердое тело – это совокупность материальных точек и при его вращении вокруг неподвижной оси каждая из них движется по окружности, рассмотрим движение одной материальной точки по окружности.

Вектор называется вектором углового перемещения,он численно равен углу поворота, направление его определяется по правилу правого винта. Единицей измерения углового перемещения в СИ является радиан (рад).

Кинематической характеристикой направления и быстроты вращения материальной точки служит угловая скорость, которая определяется как первая производная от углового перемещения по времени: Она всегда направлена так же, как и вектор углового перемещения. Единицей измерения угловой скорости в СИ является радиан в секунду (рад/с).

В том случае, если вектор меняется с течением времени, вводят понятие углового ускорения 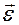, вектора характеризующего быстроту изменения угловой скорости:

Вектор углового ускорения 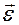совпадает по направлению с вектором угловой скорости , если движение материальной точки равноускоренное ( >0).

В случае равнозамедленного движения ( <0) вектор углового ускорения 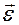направлен в сторону, противоположную вектору .

В СИ угловое ускорение измеряется в радианах на секунду в квадрате (рад/с²).

Если материальная точка движется по окружности радиуса 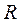, и за время перемещается из положения 1 в положение 2, то путь S, пройденный по дуге окружности, связан с углом поворота известным из курса математики соотношением . Тогда 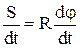или .

Продифференцировав это выражение по времени: получим выражение, связывающее угловое и тангенциальное ускорения: .

Рассмотрим полученную связь линейных и угловых величин в векторной форме. Остановимся для удобства на рассмотрении равноускоренного движения ().Применим правило правого винта. При вращении от к поступательное движение правого винта осуществляется вдоль , поэтому . Аналогично .

Нормальное ускорение противоположно по направлению радиус-вектору , следовательно:

При описании равномерного движения материальной точки по окружности и равномерного вращения тела часто используются такие величины как период (Т) и частота вращения (n или ).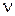

Период вращения - это время, за которое тело совершает один полный оборот. Период измеряется в СИ в секундах (с).

Частота вращения – это число оборотов, совершенное телом за единицу времени. В СИ частота вращения измеряется в с^-1 (1/с).

Если за некоторое время t тело совершило N полных оборотов, то и . Следовательно, и .

Поскольку период – это время одного полного оборота (), то . А, следовательно, .

Модули углового перемещения и угловой скорости связаны с числом полных оборотов N и частотой вращения n: