Лабораторная работа № 3-2
Измерение электрического сопротивления
проводников с помощью моста УИТСТОНА
Цель работы: изучение методики измерения электрического сопротивления проводника с помощью моста Уитстона и определение удельного сопротивления материала проводника
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Мостовой метод относится к числу наиболее совершенных и точных приемов электрических измерений, вместе с тем этот метод достаточно прост.
Области применения мостов весьма многочисленны. Например, для определения таких величин, как температура, давление, влажность измеряют электрическое сопротивление чувствительного элемента датчика,
которое зависит от этих величин (термистор, тензорезистор, датчик влажности).
Измерение электрических сопротивлений обычно проводится на
постоянном токе, в этом случае измерительный мост называется мостом Уитстона. В настоящей работе измерение электрического сопротивления проводников проводится с целью расчета их удельного электрического
сопротивления.
Немецкий физик Г. Ом экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику, пропорциональна напряжению U на концах проводника:
, (1)
где R - электрическое сопротивление проводника.
Величина электрического сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого изготовлен проводник. Для однородного цилиндрического проводника электрическое сопротивление прямо пропорционально его длине l и обратно пропорционально площади S его поперечного сечения
, (2)
где r - удельное сопротивление материала.
Удельное электрическое сопротивление – есть величина, равная электрическому сопротивлению цилиндрического проводника длиной один метр и площадью поперечного сечения один квадратный метр.
В системе СИ удельное сопротивление измеряется в Ом.м.
Мост Уитстона состоит из четырех сопротивлений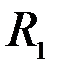 
, 
, 
, 
, соединенных между собой и образующих замкнутый четырехугольник (рис.1).
| G |
| Rx |
| R0 |
| B |
| D |
| R1 |
| R2 |
| I1 |
| I2 |
| I3 |
| I4 |
| Ig |
| I |
| K |
| А |
| С |
Рис.1. Схема моста Уитстона
В диагональ ВD четырехугольника вводится нулевой гальванометр G, в диагональ АС - источник постоянного тока и ключ К.
Электрические сопротивления R1, R2, Rx, R0 называют плечами
моста.
Ток в гальванометре Ig равен нулю тогда, когда потенциалы точек В и D одинаковы.
Такое состояние четырехугольникасопротивлений - моста Уитстона называется равновесием моста.
Покажем, что условие равновесия моста Уитстона определяется
соотношением
. (3)
Согласно первому правилу Кирхгофа алгебраическая сумма токов, сходящихся в узле, равна нулю
. (4)
На основании первого правила Кирхгофа для узлов В и D
, (5)
. (6)
При равновесии моста 
.
Следовательно, формулы (5) и (6) для равновесного состояния моста могут быть записаны в виде
, (7)
.(8)
По второму правилу Кирхгофа в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма падений напряжений на всех участках этого контура численно равна алгебраической сумме ЭДС всех источников, включенных в контур
. (9)
Второе правило Кирхгофа при равновесии моста для контуров АВD и ВСD может быть записано в виде
, (10)
. (11)
После преобразований формул (10) и (11) получим
,(12)
. (13)
Разделим эти уравнения почленно
. (14)
Так как 
и 
, то, после сокращения в обеих частях
формулы (14) получим
. (15)
Из формулы (15) следует
. (16)