Перевод чисел из десятичной системы счисления в систему счисления с основанием q и обратно

Лекция 3. Перевод чисел из одной позиционной системы счисления в другую позиционную систему счисления.

Перевод чисел из десятичной системы счисления в систему счисления с основанием q и обратно

Для перевода чисел из системы счисления с основанием q в десятичную систему счисления необходимо число представить в многочленной форме, которая представляет собой сумму m + n + 1 слагаемых. Каждое слагаемое ставится в соответствие разряду исходного числа и представляет собой произведение двух сомножителей. Первый сомножитель - десятичное число, соответствующее по весу цифре разряда исходного числа. Второй сомножитель - это степень, основанием которого является основание системы счисления, а показателем степени - номер разряда.

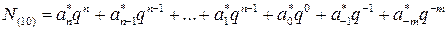
Для перевода целых чисел из десятичной в систему счисления с основанием q исходное число необходимо разделить на основание системы счисления q. При этом будет получено частное (целое число) и остаток от деления (целое число). На следующем шаге алгоритма необходимо полученное частное также разделить на основание системы счисления. Будет получено новое частное и остаток. Деление очередного частного производится до тех пор, пока очередное частное не окажется строго меньше основания системы счисления q. Цифре старшего разряда будет соответствовать частное последнего деления. Цифре следующего разряда - остаток последнего деления. Цифре следующего разряда - остаток предпоследнего деления и т. д., цифре младшего разряда будет соответствовать остаток первого деления.

Для перевода правильной десятичной дроби из десятичной системы счисления в систему счисления с основанием q правильную дробь необходимо умножить на основание системы счисления q. При этом будет получена целая и дробная часть произведения. На следующем шаге алгоритма необходимо дробную часть произведения умножить на основание системы счисления q. При этом будет получена также целая и дробная часть произведения. Дробные части произведений далее умножаются на основание системы счисления q.

Этот процесс завершается в трёх случаях:

1. Дробная часть произведения оказывается равной нулю. В этом случае перевод исходного десятичного числа в систему счисления с основанием q точный.

2. Дробная часть произведения оказывается равной одной из дробных частей произведений, найденных ранее. В этом случае искомое число представляет собой периодическую дробь (перевод приближенный).

3. Задана точность перевода, определяемая количеством разрядов в дробной части числа. В этом случае считается, что все разряды дробной части искомого числа определены, когда количество найденных произведений равно точности перевода.

Запишем исходное число. Цифре разряда с номером -1 соответствует целая часть первого произведения. Цифре разряда с номером -2 соответствует целая часть второго произведения, и т. д.

При вводе дробных чисел перевод в двоичную систему счисления может быть произведен приближенно, при обратном переводе из двоичной в десятичную систему счисления результат, если не производить округления, будет меньше исходного числа.

Упражнения и задачи

1. Выполнить перевод числа 101101₂ из двоичной системы счисления в десятичную систему счисления:

2. Выполнить перевод числа 2312₈ из восьмеричной системы счисления в десятичную систему счисления.

3. Выполнить перевод числа 1dc₁₆ из шестнадцатеричной системы счисления в десятичную систему счисления.

4. Выполнить перевод числа 891₁₀ из десятичной системы счисления в двоичную систему счисления:

5. Выполнить перевод числа 891 из десятичной системы счисления в восьмеричную систему счисления:

6. Выполнить перевод числа 891₁₀ из десятичной системы счисления в шестнадцатеричную систему счисления:

7. Перевести из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления и обратно из полученных представлений в десятичную систему счисления. Перевод производить с точностью: для шестнадцатеричной системы счисления до 2-х знаков, для восьмеричной системы счисления – до 3 знаков, для десятичной системы счисления – до 5 знаков. Сравнить результаты, полученные после перевода в десятичную систему счисления с исходным числом. Определить относительную ошибку перевода.

Решение задачи №1:

Выполнить перевод числа 101101₂ из двоичной системы счисления в десятичную систему счисления:

_{5 4 3 2 1 0}

101101₂ = 1´2⁵ + 0´2⁴ + 1´2³ +1´2² + 0´2¹ +1´2⁰ =

= 32 + 0 + 8 + 4 + 0 + 1 = 45_10.

Проверим результат перевода:

1.) 45:2 = 22 (1);

2.) 22:2 = 11 (0);

3.) 11:2 = 5 (1);

4.) 5:2 = 2 (1);

5.) 2:2 = 1 (0).

Запишем число в двоичной системе счисления: 45₁₀ = 101101_2. Проверка подтверждает правильность решения.

Ответ: 101101₂ = 45₁₀.

Решение задачи № 2

Выполнить перевод числа 2312₈ из восьмеричной системы счисления в десятичную систему счисления.

_{3 2 1 0}

2312₈ = 2 ´ 8³ +3 ´ 8² +1 ´ 8¹ +2 ´ 8⁰ = 1024+192+8+2=1226_10.

Проверим результат перевода:

1.) 1226:8 = 153 (2);

2.) 153:8 = 19 (1);

3.) 19:8 = 2 (3);

 

Запишем число в восьмеричной системе счисления: 1226₁₀= 2312_8. Проверка подтверждает правильность решения.

Ответ: 2312₈. = 1226_10.

Решение задачи № 3

Выполнить перевод числа 1dc₁₆ из шестнадцатеричной системы счисления в десятичную систему счисления.

_{2 1 0}

1dc₁₆ = 1 ´ 16² + 13 ´ 16¹ +12 ´ 16⁰ = 256+208+12 = 476_10.

Проверим результат перевода:

1.) 476:16 = 29 (12);

2.) 29:16 = 1 (13).

 

Запишем число в шестнадцатеричной системе счисления: 476₁₀= 1dc_16. Проверка подтверждает правильность решения.

Ответ: 1dc₁₆ = 476₁₀.

Решение задачи № 4

Выполнить перевод числа 891₁₀ из десятичной системы счисления в двоичную систему счисления:

1) 891:2 = 445 (1), 445 >= 2;

2) 445:2 = 111 (0), 111 >= 2;

3) 111:2 = 55 (1), 55 >= 2;

4) 55:2 = 27 (1), 27 >= 2;

5) 27:2 = 13 (1), 13 >= 2;

6) 13:2 = 6 (1), 6 >= 2;

7) 6:2 = 3 (0), 3 >= 2;

8) 3:2 = 1 (1), 1 < 2 – конец перевода.

Запишем результат перевода: 981₁₀ = 1101111011_2.

Проверим результат перевода:

_{9 8 7 6 5 4 3 2 1 0}

1101111011₂ =1´2⁹+1´2⁸+0´2⁷ +1´2⁶ +1´2⁵+1´2⁴+1´2³+0´2²+1´2¹+1´2⁰ =

= 512 + 256 + 0 + 64 + 32 + 16 + 8 + 0 + 2 + 1 = 981_10..

Проверка подтверждает правильность решения.

Ответ: 891₁₀ = 1101111011₂.

 

Решение задачи № 5

Выполнить перевод числа 891 из десятичной системы счисления в восьмеричную систему счисления:

1) 891:8 = 111 (3), 111 >= 8;

2) 111:8 = 13 (7), 13 >= 8;

3) 13:8 = 1 (5), 1 < 8 – конец перевода.

Запишем результат перевода: 891₁₀ = 5173₈

Проверим результат перевода:

_{3 2 1 0}

1573₈ = 1 ´ 8³ + 5 ´ 8² + 7 ´ 8¹ + 3 ´ 8⁰ = 512 +320 + 56 + 3 = 891_10.

Проверка подтверждает правильность решения.

Ответ: 891₁₀ = 1573_8.

Решение задачи № 6

Выполнить перевод числа 891₁₀ из десятичной системы счисления в шестнадцатеричную систему счисления:

1) 891:16 = 55 (11), 55 >= 16;

2) 55:16 = 3 (7), 3 < 16 – конец перевода.

Запишем результат перевода: 891₁₀ = 37b₁₆

Проверим результат перевода:

_{2 1 0}

37b₁₆ = 3 ´ 16² + 7 ´ 16¹ +11 ´ 16⁰ = 768 + 112 + 11 = 891_10.

Проверка подтверждает правильность решения.

Ответ: 891₁₀ = 37b_16.

Решение задачи № 7

Перевести из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления и обратно из полученных представлений в десятичную систему счисления. Перевод производить с точностью: для шестнадцатеричной системы счисления до 2-х знаков, для восьмеричной системы счисления – до 3 знаков, для десятичной системы счисления – до 5 знаков. Сравнить результаты, полученные после перевода в десятичную систему счисления с исходным числом. Определить относительную ошибку перевода.

1. Выполнить перевод числа 17.97 из десятичной системы счисления в двоичную систему счисления.

1.1. Переводим целую часть числа:

1) 17: 2 = 8 (1), 8 >= 2;

2) 8: 2 = 4 (0), 4 >= 2;

3) 4: 2 = 2 (0), 2 >= 2;

4) 2: 2 = 1 (0), 1< 2 – конец перевода.

Итак, 17₁₀ = 10001₂

1.2. Переводим дробную часть числа:

1) 0.97 ´ 2 = 1.94 (1);

2) 0.94 ´ 2 = 1.88 (1);

3) 0.88 ´ 2 = 1.76 (1);

4) 0.76 ´ 2 = 1.52 (1);

5) 0.52 ´ 2 = 1.04 (1).

Итак, 0.97₁₀ = 0.11111₂

Таким образом, 17.97₁₀ = 10001.11111₂

2. Выполним перевод числа 17.97 из десятичной системы счисления в восьмеричную систему счисления.

2.1. Переводим целую часть числа:

1) 17: 8 = 2 (1), 2 < 8 – конец перевода.

Итак, 17₁₀ = 21₈

2.2. Переводим дробную часть числа:

1) 0.97 ´ 8 = 7.76 (7);

2) 0.76 ´ 8 = 6.08 (6);

3) 0.08 ´ 8 = 0.64 (0);

Итак, 0.97₁₀ = 0.760₈

Таким образом, 17.97₁₀ = 21.760₈

3. Выполним перевод числа 17.97 из десятичной системы счисления в шестнадцатеричную систему счисления.

3.1. Переводим целую часть числа:

1) 17: 16 = 1 (1), 1 < 16 – конец перевода.

Итак, 17₁₀ = 11₁₆

3.2. Переводим целую часть числа:

1) 0.97 ´ 16 = 15.52 (15);

2) 0.52 ´ 16 = 8.32 (8);

Итак, 0.97₁₀ = f8₁₆

Таким образом, 17.97₁₀ = 11.f8₁₆

4. Выполним перевод числа 1001.11111 из двоичной системы счисления в десятичную систему счисления:

_{4 32 1 0 -1-2-3 –4 -5}

10001.11111 ₂ = 1 * 2⁴ + 0 * 2³ + 0 * 2² + 0 * 2¹ +1 * 2⁰ +1 * 2^-1 +1 * 2^-2 + 1 *2^-3 + 1 * 2^-4 + 1 * 2^-5 = 16+0+0+0+1+0.5+0.25+0.125+0.0625+0.03125 = 17.96875₁₀.

Запишем искомое число: 10001.11111₂ = 17.96875_10,

Имеем: 17,97 ≠ 17,96875

5. Вычислим относительную ошибку E:

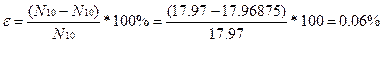
6. Выполним перевод числа 21.760 из восьмеричной системы счисления в десятичную систему счисления.

_{1 0 -1-2-3}

21.760₈ = 2 ´ 8¹ + 1´ 8⁰ + 6 ´ 8^-2 + 0.8^-3 = 16 + 1 + 0.875 + 0.09375 + 0 = 17.96875₁₀.

Запишем искомое число: 21.760₈ = 17.96875₁₀

Имеем: 17.97 ≠ 17.96875

7. Вычислим относительную ошибку E:

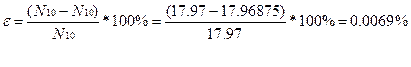
8. Выполним перевод числа 11.f8 из шестнадцатеричной системы счисления в десятичную систему счисления:

_{1 0 -1-2}

11.f8₁₆ = 1 ´ 16¹ + 1 ´ 16⁰ + 15 ´ 16 ^–1 + 8 ´16^-2 = 16 + 1 + 0.9375 + 0.03125 = 17.96875₁₀

Запишем искомое число: 11.f851e₁₆ = 17.96875₁₀

Имеем: 17.97 ≠ 17.96875

9. Вычислим относительную ошибку E:

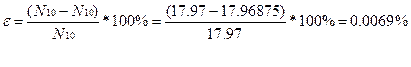
Перевод чисел из двоичной системы счисления в систему счисления с основанием 2ⁿ и обратно

Для перевода чисел из двоичной в восьмеричную и шестнадцатеричную систему счисления необходимо разбить исходное число на триады (тетрады). Триада (тетрада) представляет собой последовательность трех (четырех) соседних двоичных цифр взятых из записи исходного числа.

Разбиение исходного числа производится от разделительной точки. Целая часть числа разбивается при движении от разделительной точки влево. Дробная часть числа разбивается при движении от разделительной точки вправо. Крайняя левая группа, если она не укомплектована двоичными цифрами, дополняется нулями: слева. Крайняя правая группа, если она не укомплектована двоичными цифрами, дополняется нулями: справа. Далее необходимо каждой триаде (тетраде) поставить в соответствие цифру восьмеричной (шестнадцатеричной) системы счисления. Запишем число. Порядок цифр восьмеричных (шестнадцатеричных) цифр в записи искомого числа такой же, что и порядок соответствующих триад (тетрад) в записи исходного числа.

Для перевода из восьмеричной, шестнадцатеричной систем счисления в двоичную систему счисления необходимо каждой цифре исходного числа поставить в соответствие триаду (тетраду) двоичных цифр. Запишем искомое число. Искомое число будет состоять из последовательности триад (тетрад). Порядок триад такой же, как и порядок соответствующих цифр в записи исходного числа.

Упражнения и задачи

1. Выполнить перевод числа 101101₂ из двоичной системы счисления в восьмеричную систему счисления:
2. Выполнить перевод числа 101101₂ из двоичной системы счисления в шестнадцатеричную систему счисления:
3. Выполнить перевод числа 2312₈ из восьмеричной системы счисления в двоичную систему счисления:
4. Выполнить перевод числа 1dc₁₆ из шестнадцатеричной системы счисления в двоичную систему счисления:

Решение задачи №1

Разобьем исходную запись числа на триады двоичных разрядов:

101101 à 101 101.

Поставим в соответствие каждой триаде восьмеричную цифру:

101₂ à 5₈;

101₂ à 5_8.

Запишем число: 101101₂ = 55₈.

Проверим результат перевода:

Поставим в соответствие каждой восьмеричной цифре триаду:

5₈ à 101₂;

5₈ à 101₂;

Запишем число: 55₈ = 101101₂.

Проверка подтверждает правильность решения.

Ответ: 101101₂ = 55_8.

Решение задачи № 2

Разобьем исходную запись числа на тетрады двоичных разрядов:

101101 à 0010 1101

Поставим в соответствие каждой тетраде шестнадцатиричную цифру:

0010₂ à 2₁₆;

1101₂ à d₁₆

Запишем искомое число: 101101₂ = 2d₁₆.

Проверим результат перевода:

Поставим в соответствие каждой восьмеричной цифре триаду:

2₁₆ à 0010₂;

d₁₆ à 1101₂;

Запишем число: 2d₁₆ = ₂. 101101_2.

Проверка подтверждает правильность решения.

Ответ: 101101₂ = 2d_16.

Решение задачи № 3

Каждой цифре в записи числа поставим в соответствие триаду двоичных цифр:

2₈ à 010₂;

3₈ à 011₂;

1₈ à 001₂;

2₈ à 010₂.

Запишем искомое число: 2312₈ = 10011001010₂.

Проверим результат перевода. Разобьем исходную запись числа на триады двоичных цифр:

10011001010₂à 010 011 001 010₂

Поставим в соответствие каждой триаде восьмеричную цифру:

010₂ à 2₈;

011₂ à3₈;

001₂ à 1₈;

010₂ à 2₈.

Запишем число: 10011001010₂. = 2312₈. Проверка подтверждает правильность решения.

Ответ: 2312₈ =.10011001010₂._.

Решение задачи № 4

Каждой цифре в записи числа поставим в соответствие тетраду двоичных цифр:

1₁₆ à 0001₂;

d₁₆ à 1101₂;

c₁₆ à 1100₂.

Запишем искомое число: 1dc₁₆ = 111011100₂

Проверим результат перевода. Разобьем исходную запись числа на тетрады двоичных цифр: 111011100₂ à 0001 1101 1100₂

Поставим в соответствие каждой тетраде шестнадцатеричную цифру:

0001₂ à1₁₆;

1101₂ à d₁₆;

1100₂ à c₁₆.

Запишем число: 111011100₂ = 1dc₁₆

Проверка подтверждает правильность решения.

Ответ:_. 1dc₁₆ = 111011100₂