Раздел 1. Элементы линейной алгебры
Матрицей А размера m×n называется прямоугольная таблица из m строк и n столбцов, состоящая из чисел или иных математических выражений aij (называемых элементами матрицы):
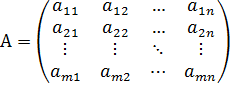 .
.
Квадратной матрицей n -го порядка называется матрица размера n×n, например, В= 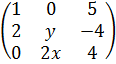 – квадратная размера 3×3.
– квадратная размера 3×3.
Диагональной называется квадратная матрица, у которой все элементы вне главной диагонали (т. е. с индексами i≠j) равны 0, например, 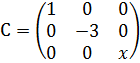 .
.
Единичной (обозначается Е) называется диагональная матрица с единицами на главной диагонали, например, 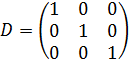 .
.
Нулевой называется матрица, все элементы которой равны 0, например, 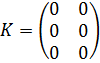 .
.
§1. Операции над матрицами.
Суммой матриц A=(aij) и B=(bij) одинакового размера называется матрица C=(cij) того же размера, причём cij= aij+ bij.
Произведением матрицы А=(aij) на число λ называется матрица B=(bij) того же размера, что и матрица А, причём bij=λ aij.
Произведением матриц А∙В (размеров m×n и n×r соответственно) называется матрица С размера m×r, такая, что cij= 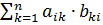 .
.
Произведение матриц А∙В существует, только если число столбцов матрицы A равно числу строк матрицы В.
Пример № 1. Найти произведение матриц А∙В и В∙А(если это возможно),если А= 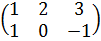 , В=
, В= 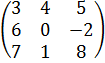 .
.
Решение. Число столбцов матрицы А равно числу строк матрицы В, поэтому произведение А∙В существует. Найдём это произведение:
А∙В= 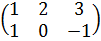 ∙
∙ 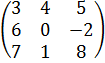 =
= 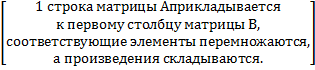 =
= 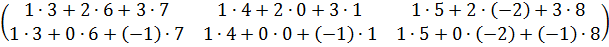 =
= 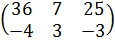 .
.
Произведение В∙А не существует, т. к. число столбцов матрицы В(3) не совпадает с числом строк матрицы А (2).
Коммутирующими (или перестановочными) называются матрицы А и В, для которых АВ=ВА.
Транспонированной к матрице А=  называется матрица
называется матрица 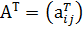 , такая, что
, такая, что 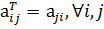 (т. е. все строки которой равны соответствующим столбцам матрицы А).
(т. е. все строки которой равны соответствующим столбцам матрицы А).
Пример № 2. Транспонировать матрицу 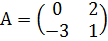 .
.
Решение. Записывая первую и вторую строки матрицы А как первый и, соответственно, второй столбец матрицы 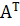 , получим матрицу
, получим матрицу 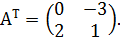
Задание № 1(пример). Найти значение матричного многочлена f(A), если 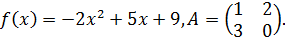
Решение. 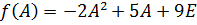 , где
, где  – единичная матрица.
– единичная матрица.
1) 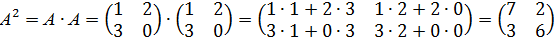 .
.
2) 
3) 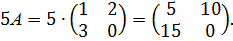
4) 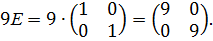
5) 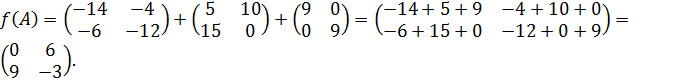
Ответ. 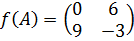 .
.
§2. Определители.
Любой квадратной матрице n -го порядка 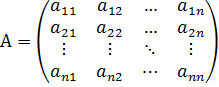 можно поставить в соответствие выражение, которое называется определителем (детерминантом) матрицы А, и обозначается так: А=
можно поставить в соответствие выражение, которое называется определителем (детерминантом) матрицы А, и обозначается так: А=  или |A| или det A.
или |A| или det A.
Вычисление определителей. Определитель матрицы A размера 2 x 2 (определитель 2-го порядка) – это число, которое можно найти по правилу:
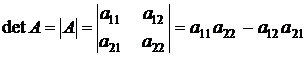
(произведение элементов, стоящих на главной диагонали матрицы, минус произведение элементов, стоящих на побочной диагонали).
Определитель матрицы A размера 3 x 3 (определитель 3-го порядка) – число, вычисляемое по правилу «раскрытие определителя по первой строке»:
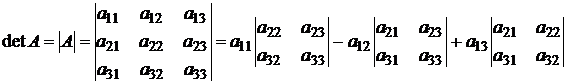
Задание №2 (пример). Вычислить определитель: 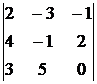
Решение. При нахождении определителя воспользуемся сначала формулой 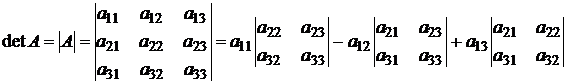 , а затем (для вычисления определителей 2-го порядка) формулой
, а затем (для вычисления определителей 2-го порядка) формулой 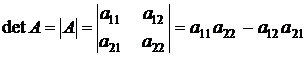 .
.
Запишем это так: det A= 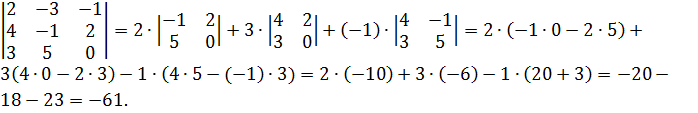
Ответ. Det A= ‒61.
Тема 1.2 Решение систем линейных уравнений по методу Крамера.
Пусть система из n линейных уравнений с n неизвестными задана в матричной форме: AX=B, где A=(aij) – матрица коэффициентов системы размера n×n, 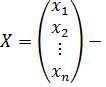 столбец неизвестных,
столбец неизвестных, 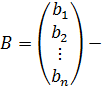 столбец свободных членов.
столбец свободных членов.
Если D – определитель матрицы А – не равен нулю, то система совместна и определена, её решение задаётся формулой: 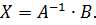
Другую форму записи этого утверждения дают формулы Крамера:
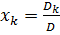 , k= 1, 2, …, n, где Dk – определитель, получающийся из D заменой k- го столбца на столбец свободных членов.
, k= 1, 2, …, n, где Dk – определитель, получающийся из D заменой k- го столбца на столбец свободных членов.
Задание №3 (пример). Решить систему уравнений по формулам Крамера и с помощью обратной матрицы: 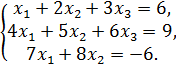
Решение.
а) Решим систему по формулам Крамера. Для этого найдём определитель матрицы системы: 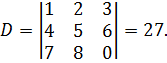 Так как D ≠0, то система совместна и определена. Найдём определители D1, D2, D3 подставляя столбец свободных членов
Так как D ≠0, то система совместна и определена. Найдём определители D1, D2, D3 подставляя столбец свободных членов 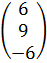 вместо первого, второго и третьего столбцов определителя D соответственно:
вместо первого, второго и третьего столбцов определителя D соответственно:
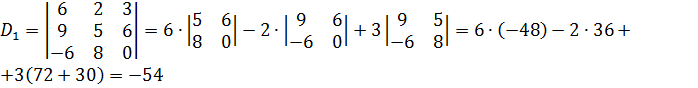 ,
,
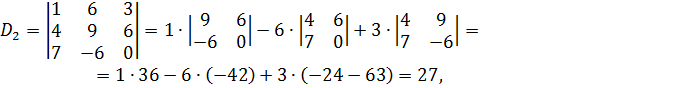
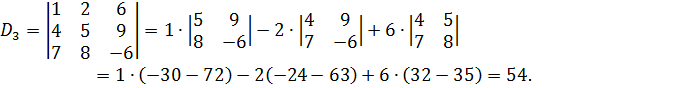
Отсюда получаем решение системы уравнений:
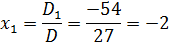
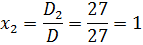
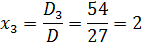
Ответ. (̶ 2; 1; 2).
Практические задания
1. Найти значение матричного многочлена: 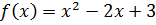 , A=
, A= 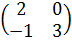 . Задание выполняем по действиям, как показано в примере.
. Задание выполняем по действиям, как показано в примере.
1. Вычислить определитель: 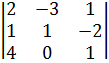
2. Решить систему уравнений по формулам Крамера:
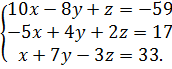
ПОМНИТЕ, ЦЕЛЬ ВЫПОЛНЕНИЯ ДАННЫХ ЗАДАНИЙ – ПОНЯТЬ ИНАУЧИТЬСЯ! ЭТО НЕ КОНТРОЛЬНАЯ РАБОТА! ЕСЛИ ЧТО-ТО НЕ ПОЛУЧАЕТСЯ, СПРОСИТЕ В ЛИЧНОМ СООБЩЕНИИ!