Прежде всего, изучите разделы 11.3 и 11.4 пособия “Математический анализ” (файл Мат.ан.2013.pdf) – с. 99 - 101.
Все определения, утверждения и примеры этих разделов приводятся для случая вещественной переменной, но они практически дословно переносятся на случай комплексной переменной, с учетом того, что на случай комплексной переменной естественным образом обобщаются понятия производной и первообразной (определения выглядят так же). При этом, конечно сохраняются формулы дифференцирования и интегрирования степенной функции.
Таким образом, получены следующие результаты
Если ряд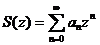 
сходится в круге 
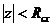, то эта аналитическая функция имеет в том же круге производную 
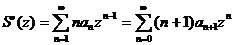(второе равенство получается заменой n на n+1) и первообразную 
.
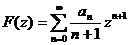Сохранение радиуса сходимости для производной нетрудно обосновать с помощью Предложения 11.1а из предыдущей лекции. Действительно, если для исходного ряда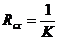 
, где 
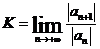, то для ряда 
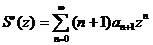радиус сходимости 
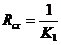где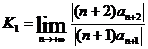 
= 
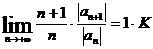. (Здесь используется замена n+1 на n.) Аналогичным образом это делается для первообразной.
Итак, операцию дифференцирования степенного ряда можно повторять внутри его области сходимости любое число раз. Таким образом, аналитическая функция в своей области определения имеет производные любого порядка.
Если аналитическая функция записана в виде степенного ряда, то коэффициенты этого ряда легко выражаются через производные этой функции (см. конец раздела 11.3 пособия). В результате получается представление аналитической функции в виде ряда Тейлора
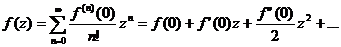
(В отличие от формулы, полученной в пособии, здесь считается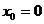 
, а вещественная переменная x заменяется на комплексную z.) (Если вспомнить материал прошлого семестра, то можно сказать, что представление функции в виде ряда Тейлора – это формула Тейлора порядка бесконечность.)
|
|
Если функция вещественной переменной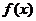 
имеет в точке 0 производные любого порядка, то, при определенных ограничениях на величину всех производных, она совпадает со своим рядом Тейлора на интервале сходимости этого ряда (см. Теорему 11.4 пособия). Если заменить вещественную переменную x на комплексную z, то получится аналитическое продолжение 
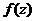функции 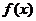на область сходимости ее ряда Тейлора на комплексной плоскости.
Итак, запись вещественной функции в виде ряда Тейлора (разложение в ряд Тейлора) с одной стороны само по себе используется в различных приложениях (о чем пойдет речь на следующей лекции), а с другой стороны позволяет расширять область определения известных функций с вещественной прямой на комплексную плоскость.
Известные соотношения между функциями вещественной переменной в виде тождеств (например, тригонометрические формулы) естественно переносятся на соответствующие степенные ряды и, тем самым, на комплексные значения переменных. Однако, этого нельзя сказать о неравенствах: расширение области определения на комплексные значения может привести к потере смысла или нарушению известных неравенств для функций вещественных переменных.
В заключение лекции приведу ряды Тейлора для некоторых элементарных функций с указанием области, где такое представление справедливо (области сходимости ряда), а также места в пособии, где можно найти вывод соответствующей формулы. Эти представления полезно запомнить, они часто используются для решения практических задач, а также будут использоваться на следующей лекции.
|
|
, 
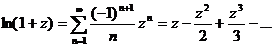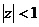(Пример11.2, с.99)
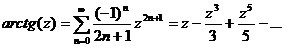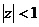, (Пример11.2, с.99)
, 
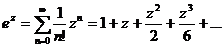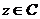(Предложение11.2, с.101)
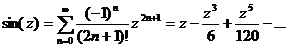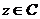, (Предложение11.2, с.101)
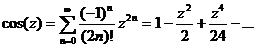
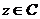(Предложение11.2, с.101)