Для практических занятий по курсу
Основы научных исследований в агрономии
Смоленск 2012
УДК 631/. 635(075.8)
ББК 41.4я73
В96
Рецензент: Юденков А.В., доктор физико-математических наук, заведующий кафедры информационных технологий и высшей математики ФГБОУ ВПО «Смоленская государственная сельскохозяйственная академия».
Вьюгин С.М.
В96 Рабочая тетрадь для практических занятий по курсу «Основы научных исследований в агрономии». Издание второе дополнительное и переработанное. / С.М. Вьюгин. – Смоленск: ФГБОУ ВПО «Смоленская ГСХП», 2012.
Рабочая тетрадь предназначена для студентов агрономических и технологических специальностей сельскохозяйственных вузов. В тетради изложены основные методы математической статистики для анализа экспериментальных данных в агрономических и смежных и ней отраслях науки. Представлены дополнительные и переработанные методики расчетов непараметрических критериев с использованием простейших средств счетной работы.
Печатается по решению методического совета ФГБОУ ВПО «Смоленская ГСХА» (протокол №7 от 30 апреля 2012 г.)
© Вьюгин С.М., 2012.
©Федеральное государственное
бюджетное образовательное учреждение
высшего профессионального образования
«Смоленская государственная
сельскохозяйственная академия»-
Вьюгин Сергей Михайлович
РАБОЧАЯ ТЕТРАДЬ
Для практических занятий по курсу
Основы научных исследований в агрономии
Издание второе дополненное и переработанное
Печатается по решению редакционно-издательского совета ФГБОУ ВПО «Смоленская государственная сельскохозяйственная академия» (протокол от №).
Предназначается для студентов инженерно-технологического факультета сельскохозяйственных вузов.
Рецензент: Юденков Алексей Витальевич, доктор физико-математических наук, заведующий кафедрой информационных технологий и высшей математики ФГБОУ ВПО «Смоленская государственная сельскохозяйственная академия».
Перечень символов, применяемых при математической обработке опытных данных.
μ – средняя генеральной совокупности;
σ2 – дисперсия генеральной совокупности;
σ- стандартное отклонение генеральной совокупности;
Х- значение варьирующего признака;
 - выборочная средняя;
- выборочная средняя;
S2 – выборочная дисперсия;
S – выборочное стандартное отклонение;
V – коэффициент вариации, изменчивости;
 - средняя ошибка выборочной средней;
- средняя ошибка выборочной средней;
 % - относительная ошибка выборочной средней;
% - относительная ошибка выборочной средней;
d – разность между выборочными средними;
l – число вариантов;
n- повторность, объем выборки;
N – общее число наблюдений в опыте;
ν – число степеней свободы;
t – критерий Стьюдента;
F - -критерий Фишера;
НСР – наименьшая существенная разность;
С – корректирующий фактор;
Су, Ср, Сv, Сz и т.д. – суммы квадратов отклонений для разных источников варьирования в дисперсионном анализе;
r – коэффициент линейной корреляции;
вху – коэффициент регрессии У по Х;
Ссоv – ковариация;
∑- сумма, знак суммирования;
÷ - доверительный интервал.
Содержание
| Работа 1. Статистические характеристики вариационных рядов и группировка данных при количественной изменчивости……… | |
| Работа 2. Оценка существенности средних двух зависимых (I) и независимых (II) выборок при количественной изменчивости….. | |
| Работа 3. Статистический анализ вариационных рядов при качественной изменчивости…………………………………………….. | |
| Работа 4. Непараметрические критерии для проверки нулевой гипотезы (по Усманову Р.Р. и др., 1985)………………………… | |
| Работа 5. Дисперсионный анализ данных вегетационного опыта с одинаковой и разной повторностью по вариантам……………… | |
| Работа 6.Дисперсионных анализ данных полевого опыта, с полным набором дат, проведенного методом рендомизированных повторений……………………………………………………… | |
| Работа 7.Дисперсионный анализ данных полевого опыта с выпавшими из учета датами, проведенного методом рендомизированных повторений………………………………………………… | |
| Работа 8.Дисперсионный анализ данных полевого опыта с повышенной повторностью варианта, проведенного методом рендомизированных повторений……………………………………… | |
| Работа 9. Дисперсионный анализ данных полевых опытов, проведенных методом латинского квадрата или латинского прямоугольника…………………………………………………………….. | |
| Работа 10. Дисперсионный анализ данных с неоднородными выборками (анализ данных, которые на подчиняются закону нормального распределения)……………………………………….. | |
| Работа 11.Дисперсионный анализ данных двухфакторного опыта проведенного методом рендомизированных повторений…….. | |
| Работа 12.Дисперсионный анализ данных двухфакторного опыта, проведенного методом расщепленных делянок………………. | |
| Работа 13. Корреляционный и регрессионный анализ (прямолинейная корреляция)…………………………………………………. | |
| Работа 14.Ковариационный анализ……………………………….. | |
| Работа 15.Оценка соответствия между эмпирическими и теоретическими распределениями по критерию Пирсона (χи- квадрат). | |
| Работа 16..Пробит-анализ | |
| Работа 17.Планирование полевого опыта | |
| Вопросы для самоподготовки | |
| Шифр задания |
Основная литература
1. Кирюшин Б.В. и др. Основы научных исследований в агрономии / Б.Д. Кирюшин, Р.Р. Усманов, И.П. Васильев. – М.: КолосС, 2009. – 398 с.
2. Доспехов Б.А. Методика полевого опыта (с основами статистической обработки результатов исследований): учебник / Б.А. Доспехов - М., Агропромиздат, 1985. – 416 с.
Дополнительная литература
1. Литл Т.Сельскохозяйственное опытное дело (Планирование и анализ): учебник / Литл Т., Хиллз Ф. – М:. Колос, 1981. – 385 с.
2. Перегудов В.Н. Планирование многофакторных полевых опытов с удобрениями и математическая обработка их результатов: учебник / В.Н. Перегудов. - М., Колос, 1968. -157 с.
3. Вьюгин С.М. и др. Непараметрические методы статистики в агрономии / С.М. Вьюгин, А.В. Юденков. – Смоленск, 2004. – 100 с.
Вьюгин С.М. и др. Статистическая обработка результатов научных исследований в агрономии / С.М. Вьюгин, А.В. Юденков, А.М. Володченков. – Смоленск, 2006. – 117 с.
Работа 1. Статистические характеристики вариационных рядов и группировка данных при количественной изменчивости
Литература. Доспехов Б.А. с. 179-192; с. 195-201; с. 204 – 217.
1. Нормальное распределение и его закономерности
2. Вариационный ряд. Понятие и виды количественной изменчивости.
3. Генеральная совокупность и выборка
4. Статистические характеристики количественной изменчивости (формулы и определения)
Цель работы. Освоить группировку данных, полученных в результате наблюдений, рассчитать статистические показатели, построить гистограмму и вычертить кривую распределения вариационного ряда.
Пример. Масса клубней картофеля, г.
Шифр задания ___________ Подпись преподавателя ____________
Порядок выполнения работы
Рабочая таблица
| Шифр задания | Значения признака, Х |
Число классов 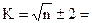
Классовый интервал 
Таблица для расчетов (А=).
| номер группы | группа | частота, f | среднее по группам, Х | х1= Х-А | f.x1 |  
| 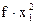
|
| Суммы | 
| - | 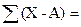
| 
| - | 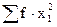
|
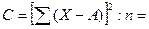
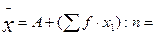
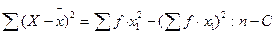


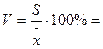
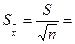


| Частота, f |
Значение признака Х
Гистограмма и кривая распределения
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
Дата сдачи работы ____________ Подпись преподавателя________________
Работа 2. Оценка существенности средних двух зависимых (I) и независимых (II) выборок при количественной изменчивости.
Литература. Доспехов Б.А. стр. 220-230; 250-252.
1. Точечная и интервальная оценка параметров распределения.
2. Понятие о нулевой гипотезе и статистические методы ее проверки.
3. Примеры зависимых и независимых выборок.
4. Оценки существенности разности средних зависимых и независимых выборок по критерию Стьюдента.
I) зависимые выборки
Цель работы. Согласно заданию вычислить статистические характеристики для двух зависимых выборок. Определить существенны ли разности между средними и сделать статистический и агрономический выводы.
Пример 1. Пораженность двух сортов ячменя корневыми гнилями. Сорта располагались по соседним делянкам.
| № пары | Зазерский 85, Х1 | Биос – 1, Х2 | Разность d=Х2-Х1 | Квадрат разности, d2 |
| 43,5 | 36,2 | |||
| 41,4 | 35,6 | |||
| 39,8 | 36,4 | |||
| 45,6 | 33,0 | |||
| 61,1 | 38,5 | |||
| 34,1 | 39,7 | |||
| 43,8 | 35,7 | |||
| 39,4 | 36,5 | |||
| 41,5 | 34,6 | |||
| 41,4 | 34,8 | |||
| 52,5 | 41,3 | |||
| 47,6 | 32,8 | |||
| 44,1 | 36,8 | |||
| 42,4 | 34,7 | |||
| 45,6 | 35,5 | |||
| Суммы | ∑Х1= | ∑Х2= | ∑d= | ∑d2 = |
| Средние | 
| 
| 
|
Порядок выполнения работы
1. По каждому вариационному ряду находим число наблюдений N1=
N2= /
2. Определяем суммы наблюдений и рассчитываем выборочные средние по сортам 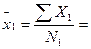

3. Определяем отклонения для каждой сопряженной пары наблюдений и вычисляем среднюю разность
 , где N - число пар наблюдений.
, где N - число пар наблюдений.
4. Для определения ошибки средней разности находим:
Корректирующий фактор
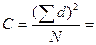
Сумму квадратов разностей
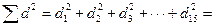
Ошибку средней разности
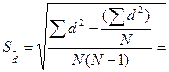
5. Проводим оценку существенности средней разности по фактическому критерию Стьюдента
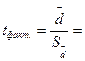
По таблице приложения 1 находим теоретические значения критерия Стьюдента при числе степеней свободы N-1= t05= и t01=
6. Проверяем правильность оценки существенности по величине наименьшей существенной разности 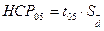 =
= 
Выводы
Дата сдачи работы__________ Подпись преподавателя_________
II) Независимые выборки.
Цель работы. Определить статистические характеристики для двух независимых выборок. Оценить существенность разности средних и сделать статистический и агрономический выводы.
Пример 2. Глубина заделки семян яровой пшеницы после вспашки на 20 см и дискования на 10-12 см. Дать оценку качества посева яровой пшеницы по обработкам.
| № | Вспашка на 20 см, Х1 | 
| Дискование на 10-12 см, Х2 | 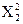
|
| 4,5 | 4,6 | |||
| 5,8 | 3,6 | |||
| 5,6 | 3,2 | |||
| 4,9 | 5,1 | |||
| 3,0 | 4,4 | |||
| 5,9 | 3,8 | |||
| 7,4 | 3,3 | |||
| 3,9 | 4,4 | |||
| 5,0 | 3,7 | |||
| 8,1 | 5,5 | |||
| 4,3 | 2,1 | |||
| 7,2 | 2,9 | |||
| 4,7 | 5,3 | |||
| 5,6 | 1,7 | |||
| 7,2 | 0,9 | |||
| Суммы |
Порядок выполнения работы
По каждой выборке находим:
| № | Статистические показатели | Вспашка на 20 см, Х1 | Дискование на 10-12 см, Х2 |
| Число наблюдений, N | |||
Средняя арифметическая
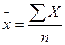
| |||
Корректирующий фактор

| |||
Сумма квадратов отклонений

| |||
Дисперсия 
| |||
Стандартное отклонение

| |||
Ошибка выборочной средней

| |||
Коэффициент вариации
 % %
| |||
Доверительный интервал для генеральной средней

| |||
Доверительный интервал для генеральной совокупности

|
Оценка существенности различий между средними.
1. Интервальным методом

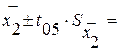
2. По критерию существенности Стьюдента
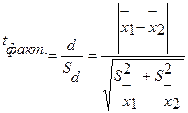
t05=
t01= при γ= N1+N2-2
3. По величине наименьшей существенности разности (НСР)

НСР05=t05.Sd
НСР01=t01.Sd
Выводы.
Дата сдачи работы. Подпись преподавателя.
Работа 3. Статистический анализ вариационных рядов при качественной изменчивости.
Литература. Доспехов Б.А.с. 192-195, с. 217-220, 230-231.
1. Качественная изменчивость. Определение и примеры.
2. Статистические характеристики качественной изменчивости. Формулы и определения.
3. Методы оценки существенной разности между выборочными долями.
Цель работы. Освоить расчеты при качественной изменчивости признака, оценить существенность разности между выборочными долями и сделать вывод.
Пример. В выборках объемом по 500 растений ячменя пораженных корневыми гнилями в севообороте и при бессменном возделывании было следующим:
| Варианты | |||||||||||||||||
| Севооборот | |||||||||||||||||
| Бессменно |
Шифр задания ____________ Подпись преподавателя__________
Порядок выполнения работы
| Севооборот | Бессменный посев |
| nб= | nб= |
| nзд.= | nзд=. |
| N1= nб+ nзд.= | N2= nб+ nзд.= |
| P1= nб: N1= | P2= nб: N2= |
| q1=1- P1 | q2=1- P2 |

| 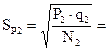
|

| 
|

| 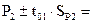
|
Оценка существенности разности между выборочными долями:
1) по критерию Стьюдента

t05=
t01= при γ= N1+N2-2
2) По величине наименьшей существенности разности (НСР)
НСР05=t05.Sd
НСР01=t01.Sd
3). Интервальным методом
Севооборот 

Бессменный посев 

Выводы:
Дата сдачи работы ___________Подпись преподавателя_____________
Работа 4. Непараметрические критерии для проверки нулевой гипотезы (по Усманову Р.Р. и др. 1985 г.)
Литература. Вольф В.Г., 1966; Лакин Г.Ф., 1980.
1. Сравнение независимых выборок по Х-критерию Ван-дер-вардена.
Пояснения к работе.
Пример. В лабораторных условиях проводилась оценка устойчивости двух сортов овса к стеблевой ржавчине. Растения опрыскивали из пульверизатора суспензией уредоспор.
На 14 день после инокуляции учитывали тип реакции в баллах по Стэкмэну и Левину.
Тип реакции в баллах
| Сорта | Номера проб (растений) | |||||||||
| Сорт А | ||||||||||
| Сорт В |
Порядок выполнения работы
1. Определяем число наблюдений по каждому вариационному ряду n1=; n2= и сумму всех наблюдений n= n1+ n2= /
2. Составляем вспомогательную таблицу, в которой ранжируем обе выборки и один вариационный ряд, каждому значению признака присваиваем порядковый номер (ранг) R.
Вспомогательная таблица для расчета Х-критерия.
| Пораженность в баллах | Ранг, R | Отношение

| Функция
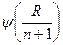
| |||||
| Сорт А | Сорт В | |||||||
| А | В | А | В | А | В | |||
| n1= | n2= | n=n1+ n2 | 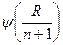 = =
|
3. Находим для всех значений признака из выборок отношение 
4. По таблице 2 определяем значения функции (ПСИ) 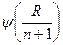
5. Суммируем с учетом знаков значения функции ∑ 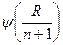
и эту сумму принимаем за фактический критерий – Х Ван-дер-Вардена.
∑ 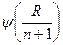 =Хф
=Хф
6. По таблице 3 находим теоретические значения Х-критерия при n=n1+ n2, с учетом разности n1- n2 и сравниваем Хф с Х05
Вывод: ______________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
Таблица 2. Значения функции 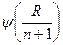

| ψ | 
| ψ | 
| ψ |
| 0,00 | 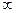
| 0,34 | -0,41 | 0,68 | 0,47 |
| 0,02 | -2,05 | 0,36 | 0,36 | 0,70 | 0,52 |
| 0,04 | -1,75 | 0,38 | -0,31 | 0,72 | 0,58 |
| 0,06 | -1,55 | 0,40 | -0,25 | 0,74 | 0,64 |
| 0,08 | -1,41 | 0,42 | -0,20 | 0,76 | 0,71 |
| 0,10 | -1,28 | 0,44 | -0,15 | 0,78 | 0,77 |
| 0,12 | -1,18 | 0,46 | -0,10 | 0,80 | 0,84 |
| 0,14 | -1,08 | 0,48 | -0,05 | 0,82 | 0,92 |
| 0,16 | -0,99 | 0,50 | 0,00 | 0,84 | 0,99 |
| 0,18 | -0,92 | 0,52 | 0,05 | 0,86 | 1,08 |
| 0,20 | -0,84 | 0,54 | 0,10 | 0,88 | 0,18 |
| 0,22 | -0,77 | 0,56 | 0,15 | 0,90 | 0,28 |
| 0,24 | -0,71 | 0,58 | 0,20 | 0,92 | 1,41 |
| 0,26 | -0,64 | 0,60 | 0,25 | 0,94 | 1,55 |
| 0,28 | -0,58 | 0,62 | 0,31 | 0,96 | 1,75 |
| 0,30 | -0,53 | 0,64 | 0,36 | 0,98 | 2,05 |
| 0,32 | -0,47 | 0,66 | 0,41 | 0,99 | 2,33 |
Таблица 3. Теоретические значения Х-критерия Ван-дер-Вардена на 5 и 1% уровне значимости.
| n=n1+ n2 | n1- n2=0 или 1 | n1- n2=2 или 3 | ||
| 0,05 | 0,01 | 0,05 | 0,01 | |
| 2,40 | - | 2,30 | - | |
| 2,48 | - | 2,40 | - | |
| 2,60 | 3,20 | 2,49 | 3,10 | |
| 2,72 | 3,40 | 2,58 | 3,40 | |
| 2,86 | 3,60 | 2,79 | 3,58 | |
| 2,96 | 3,71 | 2,91 | 3,64 | |
| 3,11 | 3,94 | 3,06 | 3,88 | |
| 3,24 | 4,07 | 3,19 | 4,05 | |
| 3,39 | 4,26 | 3,36 | 4,25 | |
| 3,49 | 4,44 | 3,44 | 4,37 | |
| 3,63 | 4,60 | 3,60 | 4,58 | |
| 3,73 | 4,77 | 3,69 | 4,71 | |
| 3,86 | 4,94 | 3,84 | 4,92 | |
| 4,39 | 5,68 | 4,36 | 5,65 | |
| 4,88 | 6,35 | 4,87 | 6,34 | |
| 5,33 | 6,95 | 5,31 | 6,92 | |
| 5,75 | 7,50 | 5,74 | 7,49 | |
| 6,14 | 8,02 | 6,12 | 8,01 | |
| 6,50 | 8,51 | 6,51 | 8,50 |
2. Сравнение независимых выборок по Т-критерию Уайта (Манна-Уитни).
Пояснения к работе
Пример 1. Проведен учет степени пораженности двух сортов озимой пшеницы бурой ржавчиной.
| Сорта | Повторность | |||||||||
| Сорт А | ||||||||||
| Сорт В | - | - |
Порядок выполнения работы
1. Располагаем все значения сравниваемых выборок в один ранжированный ряд.
2. Каждому значению присваиваем порядковый номер (ранг). Одинаковые значения признака имеют средний ранг.
Вспомогательная таблица.
| Поражения | |
| Ранг, R |
3. Определяем сумму рангов по каждой выборке (варианту)
∑R1=; ∑R2=
4. Меньшая сумма рангов принимается за Т-критерий фактический∑R=Тф=
5. По таблице 4 находим теоретическое значение Т-критерия по числу наблюдений для каждой выборки.
При n1 =;n2=; Т05= и сравниваем Тф с Т05
Выводы:
Таблица 4. Теоретические значения Т-критерия Уайта (5%-ный уровень значимости) (Данные или меньшие значения отвергают гипотезу).
| Меньшее число наблюдений – n1 | ||||||||||
| <Большее число наблюдений – n2 | ||||||||||
n1 и n2 – число наблюдений в двух группах.
Если группы неравные, то за n1 следует брать меньшее число.
3. Сравнение зависимых (сопряженных) выборок по критерию Вилкоксона.
Пояснения к работе.
Пример (по В.Г. Вольфу, 1966 г.). Десять корзинок подсолнечника перед цветением делили условно пополам. Одну половину корзинок самоопыляли пыльцой своих же цветков, а на вторую половину перед самоопылением наносили в избытке пыльцу кукурузы. Эффект дополнительного опыления определяли по числу завязавшихся семян.
Число семян подсолнечника при двух способах опыления.
| Способ опыления | № растения | |||||||||
| Самоопыление, А | ||||||||||
| Тоже + кукуруза, В | ||||||||||
| Разность, d | ||||||||||
| Ранги, R |
Порядок выполнения работы.
1. Определяем отклонения по всем сопряженным парам и записываем их со своими знаками.

2. Присваиваем порядковый номер (ранг) отклонениями d без учета знаков, при этом нулевые разности (d) рангов не имеют.
3. Определяем сумму рангов для минусовых отклонений ∑R1 = и сумму рангов для плюсовых отклонений ∑R2 =
4. Меньшую по знаку отклонений сумму рангов принимают за фактический критерий Вилкоксона ∑R =Wф.
По таблице 5 находим теоретические значение критерия Вилкоксона.
При ν=n-k = W05
И сравниваем Wф с W05
Вывод:
Таблица 5. Теоретические значения W – критерия Вилкоксона при 5% и 1% уровне значимости.
(Равные или меньшие значения приводят к опровержению Но – гипотезы)
| Число пар, n | Уровни значимости | Число пар, n | Уровни значимости | ||
| 0,05 | 0,01 | 0,01 | 0,05 | ||
| - | |||||
| - | |||||
4. Сравнение зависимых (сопряженных) выборок по Z –критерию знаков.
Пояснения к работе.
Пример 1. (по А.Е. Чумакову, И.И. Минкевич, 1977 г.). Поражение листьев яблони при инокуляции штаммами Ventura inaegualis (парша). На каждый лист наносилось по две капли суспензии спор каждого штамма.
| № | Диаметр пятна, мм | Различия(±) | |
| штамм №1 | штамм №2 | ||
Порядок выполнения работы.
1. Записывают сопряженные значения выборок (вариантов).
2. Знаками «плюс» или «минус» обозначают эффекты (различия).
3. Суммируют отдельно число плюсовых эффектов ∑ «-«=. Нулевые разности в расчет не принимают.
4. Сумму плюсовых знаков принимают за фактический критерий знаков Zф.
5. По таблице 6 определяют теоретическое значение критерия знаков Zт по числу пар, давших плюсовые и минусовые эффекты.
Вывод:
Таблица 6. Теоретические значения критерия знаков (Z) при 5% и 1% уровне значимости.
| Число пар, n | Уровни значимости | Число пар, n | Уровни значимости | ||
| 0,05 | 0,01 | 0,01 | 0,05 | ||
| - | |||||
| - | |||||
Работа 5. Дисперсионный анализ данных вегетационного опыта с одинаковой и разной повторностью по вариантам.
Литература. Доспехов Б.А. с. 242-255, 256-271.
Вопросы для самоподготовки.
1. Сущность дисперсионного анализа. Схема (модель) дисперсионного анализа данных вегетационного опыта.
2. Проверка нулевой гипотезы при дисперсионном анализе.
3. Сущность вегетационного опыта и методика его проведения.
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
4. Обработка данных в