Задача расчета: определение расчетом диаметральных размеров вала в наиболее нагруженных сечениях
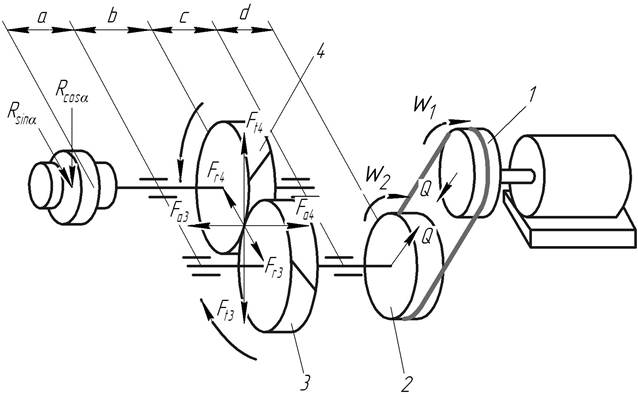
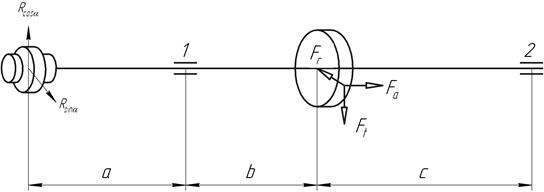
Рисунок 8.1 Пространственная схема механизма с силами, действующими на элементы кинематической цепи привода (пример)
В этой части раздела приводится пространственная схема механизма с силами, действующими на элементы кинематической цепи привода в соответствии с индивидуальным техническим заданием на курсовое проектирование по деталям машин. При этом необходимо задаться направлением вращения электродвигателя w1 и проставить на всех элементах кинематической цепи привода направления их вращения и составляющие сил в зацеплениях зубчатых колес и других передачах.
Исходные данные

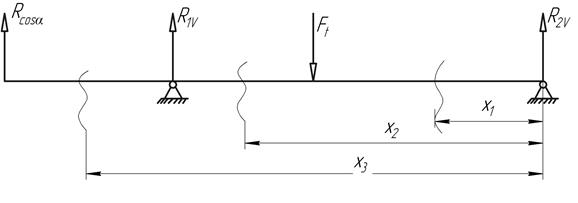
Рис. 8.2 Схема нагружения тихоходного вала редуктора
Передаваемый крутящий момент тихоходным валом Т4 ___________Н×мм
Составляющие силы в зацеплении зубчатой передачи:
Окружная сила Ft,_________ Н
Радиальная сила Fr________ Н
Осевая сила Fa ________H.
Размеры
a ________ мм (1,6хdвала)
b ________ мм (4÷5 m)
c ________ мм (4÷5 m)
Делительный диаметр зубчатого колеса d2, мм.
Если на зубчатом колесе установлена предохранительная фрикционная многодисковая муфта, размеры a, b, c берутся из чертежа (сборочный чертеж предохранительная фрикционная многодисковая муфта)
Расчет
8.1 Схематически вычерчивается тихоходный вал редуктора с элементами кинематической цепи привода и наносятся на них действующие внешние силы (рисунок 8.3, а).
8.2 Составляется расчетная схема этого вала и наносятся на нее внешние силы, опорные реакции, действующие в вертикальной плоскости (рисунок 9.3, б).
8.3 Определяются опорные реакции из условий 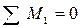 и
и  :
:

 (8.1)
(8.1)
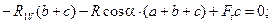
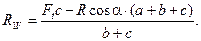 (8.2)
(8.2)
В случае отрицательной величины опорной реакции R1V или R2V, направление последней следует изменить на обратное на расчетной схеме и учитывать во всех последующих расчетах.
Произвести проверку правильности определения опорных реакций, которые должны удовлетворять условию:
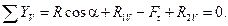
Эпюра МИV


Эпюра МИH

Рис. 8.3 Эпюры изгибающих и крутящих моментов
8.4 Составляются уравнения изгибающих моментов для различных участков вала в вертикальной плоскости.
8.4.1 Уравнение изгибающего момента для сечения I-I (рисунок 8.3, б):
 , где 0 £
, где 0 £ 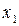 £ с;
£ с;
при 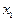 = 0
= 0 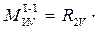 0 = 0; при
0 = 0; при 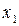 = с
= с 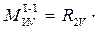 c.
c.
8.4.2 Уравнение изгибающего момента для сечения II-II:
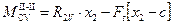 , где c £ x2 £(b + c);
, где c £ x2 £(b + c);
при x2 = c + d
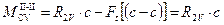 ;
;
при x2 = b + c
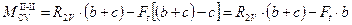
8.49.4.3 Уравнение изгибающего момента для сечения III-III:
 ,
,
где (b + c) £ x3 £(a + b + c);
при x3 = (b + c)
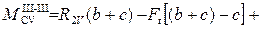
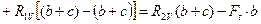 ;
;
при x3 = (a + b + c)
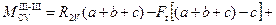
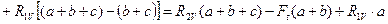 .
.
8.4.4 По расчетным значениям изгибающего момента в плоскости V строится эпюра изгибающего момента со стороны растянутых волокон (рисунок 8.3, в).
На этой эпюре необходимо привести численные значения изгибающего момента по опорам вала и зубчатому колесу.
Примечание. Так как по концам валов отсутствуют пары сил, действующих в направлении продольной оси вала, то эпюры изгибающих моментов будут иметь нулевые значения.
8.5 Вычерчивается расчетная схема вала и наносятся на нее внешние силы, действующие в плоскости Н и опорные реакции (рисунок 8.3, г).
8.6 Определяются величины опорных реакций R1H и R2H в плоскости Н исходя из условий 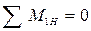 и
и 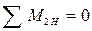 :
:
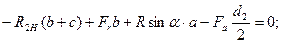 откуда
откуда
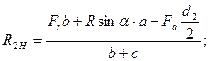 (8.3)
(8.3)
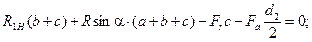 откуда
откуда
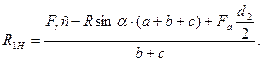 (8.4)
(8.4)
В случае отрицательной величины опорной реакции R1Н или R2Н, направление последней изменяется на обратное на расчетной схеме и учитывается во всех последующих расчетах.
Производится проверка правильности определения опорных реакций, которая должна удовлетворять условию в горизонтальной плоскости:
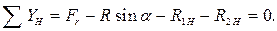
8.7 Составляются уравнения изгибающих моментов для различных участков вала в горизонтальной плоскости.
8.7.1 Уравнение изгибающего момента для сечения I-I (рисунок 9.3, г):
 , где 0 £
, где 0 £ 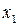 £ с;
£ с;
при  = 0
= 0 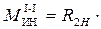 0 = 0; при
0 = 0; при 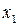 = c
= c 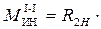 c.
c.
8.7.2 Уравнение изгибающего момента для сечения II-II:
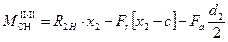 , где c £ x2 £(b + c);
, где c £ x2 £(b + c);
при x2 = c
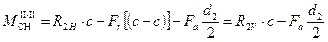 ;
;
при x2 = b + c
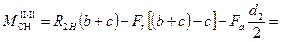
=  .
.
8.7.3 Уравнение изгибающего момента для сечения III-III:
 ,
,
где (b + c) £ x3 £ (a + b + c);
при x3 = (b + c)
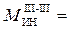
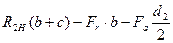 ;
;
при x3 = (a + b + c)
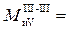
 .
.
8.7.4 По расчетным значениям изгибающего момента в плоскости Н строится эпюра изгибающего момента со стороны растянутых волокон (рисунок 8.3, д).
На этой эпюре необходимо привести численные значения изгибающего момента по опорам вала и месту установки зубчатого колеса.
8.8 Строится эпюра крутящего момента, передаваемого валом (см. рисунок 8.3, е).
8.9 Приведенный (эквивалентный) момент.
Приведенный момент определяется по наиболее нагруженным сечениям вала по зависимости:
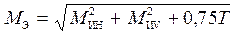 . (8.5)
. (8.5)
В рассматриваемом примере наиболее нагруженные сечения вала — опора 1 и середина вала под зубчатым колесом.
9.10 Расчет диаметральных размеров вала.
Диаметр вала по рассчитываемому сечению определяется по зависимости:
 , (8.6)
, (8.6)
где [s-1]и — допускаемые напряжения изгиба при приближенном расчете вала, [s-1]и = 50...60 Н/мм2 для валов, изготовленных из сталей Ст5, 45, 40Х, 40ХН.
Произведя расчет вала по наиболее нагруженным сечениям уточняют конструктивно его размеры. Так, например, диаметры вала под подшипниками принимают одного размера с целью уменьшения типоразмеров подшипников и упрощения технологии изготовления корпусных деталей. В связи с этим диаметр вала под зубчатым колесом не может быть меньше, чем под подшипниками.
8.11 Суммарные опорные реакции по опорам 1 и 2 составят:
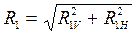 ; (8.7)
; (8.7)
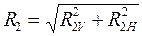 ; (8.8)
; (8.8)
при приближенном расчете вала.