Лекция 27. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами (2ч)
Содержание лекции: Интегрирование линейных однородных и неоднородных дифференциальных уравнений с постоянными коэффициентами и специально правой частью (метод неопределенных коэффициентов). Примеры.
Интегрирование линейных однородных дифференциальных уравнений.
Пусть в линейном однородном дифференциальном уравнении
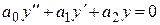
коэффициенты  – постоянные числа. Для таких уравнений доказано, что частные решения
– постоянные числа. Для таких уравнений доказано, что частные решения  ,
,  , составляющие фундаментальную систему решений, следует искать в виде
, составляющие фундаментальную систему решений, следует искать в виде  , где
, где  – корень характеристического уравнения.
– корень характеристического уравнения.
Определение 1
Характеристическим уравнением линейного однородного дифференциального уравнения 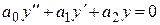 называется алгебраическое уравнение второй степени
называется алгебраическое уравнение второй степени
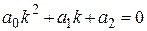 . (1)
. (1)
Характеристическое уравнение линейного дифференциального уравнения второго порядка есть квадратное уравнение, для составления которого достаточно в дифференциальном уравнении 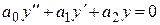 заменить
заменить 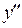 на
на 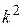 ,
, 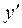 – на
– на  , а
, а  заменить на 1.
заменить на 1.
Как известно, при решении квадратного уравнения возможны три случая:
· корни 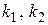 этого уравнения действительные и различные:
этого уравнения действительные и различные: 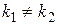 ;
;
· корни 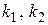 действительные и равные:
действительные и равные: 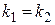 ;
;
· корни 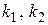 есть комплексно-сопряженные числа:
есть комплексно-сопряженные числа: 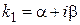 ,
, 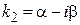 .
.
Структура фундаментальной системы решений {  ,
,  }, а вместе с ней и общего решения дифференциального уравнения (1), зависит от вида корней характеристического уравнения. Эта зависимость отражена ниже в таблице 1.
}, а вместе с ней и общего решения дифференциального уравнения (1), зависит от вида корней характеристического уравнения. Эта зависимость отражена ниже в таблице 1.
Таблица 1
| Корни характеристического уравнения | Фундаментальная система решений | Вид общего решения |
I. Действительные различные 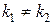
| 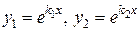
| 
|
II. Действительные равные 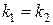
| 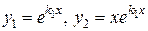
| 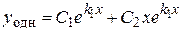
|
III. Комплексно- сопряженные
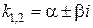
| 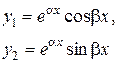
| 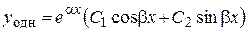
|
Предлагаем следующий порядок решения линейного однородного дифференциального уравнения:
1) Составить характеристическое уравнение для заданного дифференциального уравнения и найти его корни.
2) Записать функции  ,
,  , составляющие фундаментальную систему решений.
, составляющие фундаментальную систему решений.
3) Записать общее решение 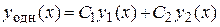 .
.
Для записи функций ФСР и общего решения используйте таблицу 3.
Пример 1. Решить дифференциальное уравнение 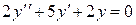 .
.
Решение
Будем придерживаться сформулированного алгоритма.
1) Составим характеристическое уравнение для данного линейного дифференциального уравнения. Для этого в уравнении 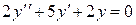 заменим
заменим 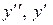 и
и 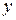 соответственно на
соответственно на 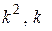 и 1, получим
и 1, получим
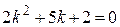 .
.
Найдем корни этого уравнения*):
 ,
,
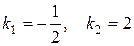 .
.
2) Полученные корни  ,
,  действительные и различные, следовательно, имеем случай I таблицы 1, поэтому фундаментальную систему решений образуют функции
действительные и различные, следовательно, имеем случай I таблицы 1, поэтому фундаментальную систему решений образуют функции
 ,
, 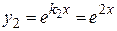 .
.
3) Тогда общим решением заданного дифференциального уравнения является функция
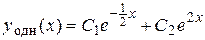 .
.
Ответ: 
Пример 2 Найти решение уравнения 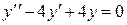 , удовлетворяющее условиям
, удовлетворяющее условиям 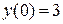 ,
, 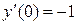 .
.
Решение
Согласно правилу решения задачи Коши вначале найдем общее решение данного уравнения.
1) Составим и решим характеристическое уравнение:
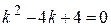 ,
,  .
.
2) Корни характеристического уравнения действительные и равные (случай II таблицы 1), следовательно, фундаментальную систему решений образуют функции
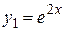 ,
, 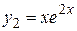 .
.
3) Тогда общее решение заданного дифференциального уравнения имеет вид
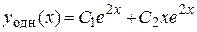 .
.
Теперь найдем искомое частное решение. Для этого нужно найти значения постоянных  и
и 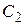 Чтобы определить эти значения, найдем производную функции
Чтобы определить эти значения, найдем производную функции 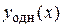 :
:
 ,
,
и подставим заданные начальные условия 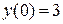 ,
, 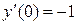 в равенства
в равенства

Получим систему уравнений относительно неизвестных  и
и 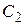 :
:
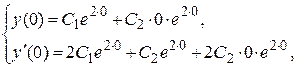 Þ
Þ 
Решив эту систему, найдем значения  и
и 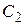 :
:
 Þ
Þ  Þ
Þ 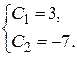
Подставим найденные значения  в общее решение
в общее решение 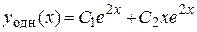 , получим искомое частное решение:
, получим искомое частное решение:
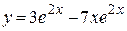 .
.
Ответ: 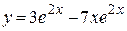
Пример 3 Решить дифференциальное уравнение  .
.
Решение
Характеристическое уравнение для данного дифференциального уравнения имеет вид
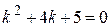 .
.
Решим это уравнение:
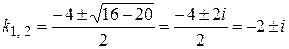 .
.
Получили комплексно-сопряженные корни (случай III таблицы 1), где  . Значит, фундаментальная система решений состоит из функций
. Значит, фундаментальная система решений состоит из функций
 ,
,  .
.
Тогда общее решение данного дифференциального уравнения имеет вид
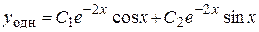 .
.
Ответ: 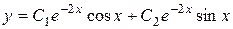 .
.
Замечание. Для линейных однородных дифференциальных уравнений

порядка выше двух (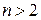 ) общее решение, аналогично уравнению второго порядка, представляет собой линейную комбинацию фундаментальной системы решений этого уравнения:
) общее решение, аналогично уравнению второго порядка, представляет собой линейную комбинацию фундаментальной системы решений этого уравнения:
 .
.
Функции  *) фундаментальной системы решений также можно найти с помощью корней характеристического уравнения, которое для уравнения п -го порядка имеет вид
*) фундаментальной системы решений также можно найти с помощью корней характеристического уравнения, которое для уравнения п -го порядка имеет вид
 .
.
Пример 4 Решить дифференциальное уравнение
 .
.
Решение
Запишем характеристическое уравнение:
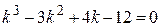 .
.
Чтобы найти корни этого уравнения, разложим на множители его левую часть, используя способ группировки и вынесения общего множителя:
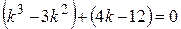 ,
, 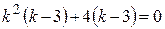 ,
,
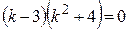 .
.
Приравнивая к нулю каждый из множителей, получаем:
1) 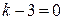 Þ
Þ 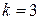 ;
;
2)  – это уравнение действительных корней не имеет, поскольку
– это уравнение действительных корней не имеет, поскольку 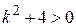 .
.
Но так как всякое алгебраическое уравнение имеет столько корней, какова его степень (в общем случае комплексных), то уравнение  имеет два комплексных корня. Найдем их
имеет два комплексных корня. Найдем их
 Þ
Þ  Þ
Þ 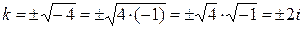 .
.
Итак, характеристическое уравнение имеет три корня:
 .
.
Запишем фундаментальную систему решений заданного дифференциального уравнения. Действительному корню 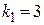 в фундаментальной системе соответствует функция–решение
в фундаментальной системе соответствует функция–решение 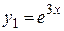 . Паре комплексно-сопряженных корней
. Паре комплексно-сопряженных корней  соответствуют два действительных решения
соответствуют два действительных решения
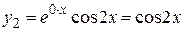 ,
,  .
.
Следовательно, общее решение заданного дифференциального уравнения имеет вид
 .
.
Ответ:  .
.
Пример 5 Решить дифференциальное уравнение 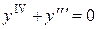 .
.
Решение
Характеристическое уравнение  , или
, или  имеет корни
имеет корни 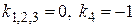 . Тогда фундаментальную систему решений образуют функции-решения
. Тогда фундаментальную систему решений образуют функции-решения
 .
.
Значит, общее решение данного дифференциального уравнения имеет вид
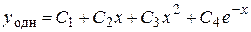 .
.
Ответ: 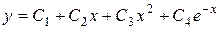
Интегрирование линейных неоднородных дифференциальных уравнений
Рассмотрим линейное неоднородное дифференциальное уравнение второго порядка
 (3.6),
(3.6),
где  – действительные числа,
– действительные числа,  непрерывная на некотором интервале
непрерывная на некотором интервале 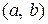 функция.
функция.
Согласно теореме 3.3 о структуре общего решения линейного неоднородного дифференциального уравнения, общее решение уравнения (3.6) можно найти в виде 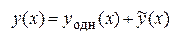 , где
, где 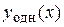 –общее решение соответствующего однородного уравнения, а
–общее решение соответствующего однородного уравнения, а 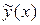 – какое-либо частное решение уравнения (3.6).
– какое-либо частное решение уравнения (3.6).
Отыскание общего решения 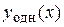 линейного однородного дифференциального уравнения рассмотрено в предыдущем пункте. Следовательно, остается решить вопрос нахождения какого-либо частного решения
линейного однородного дифференциального уравнения рассмотрено в предыдущем пункте. Следовательно, остается решить вопрос нахождения какого-либо частного решения 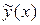 линейного неоднородного дифференциального уравнения.
линейного неоднородного дифференциального уравнения.
Для линейных неоднородных уравнений с постоянными коэффициентами в случае, когда правая часть – функция  – имеет так называемый «специальный вид» (таблица 4), можно применить метод подбора частного решения. Суть метода заключается в следующем: по виду функции
– имеет так называемый «специальный вид» (таблица 4), можно применить метод подбора частного решения. Суть метода заключается в следующем: по виду функции  и корням характеристического уравнения подбирается вид функции
и корням характеристического уравнения подбирается вид функции 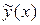 с неопределенными коэффициентами, которые затем определяются в результате подстановки
с неопределенными коэффициентами, которые затем определяются в результате подстановки 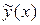 в заданное уравнение исходя из условия, что
в заданное уравнение исходя из условия, что 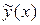 удовлетворяет уравнению (3.6).
удовлетворяет уравнению (3.6).
На практике для подбора функции 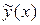 можно использовать таблицу 2.
можно использовать таблицу 2.
Рассмотрим примеры решения линейных неоднородных уравнений, придерживаясь алгоритма, сформулированного на странице 51.
Пример 6 Найти общее решение дифференциального уравнения
 .
.
Решение. Данное уравнение есть линейное неоднородное дифференциальное уравнение второго порядка. Согласно теореме 3.3, общее решение этого уравнения будем искать в виде
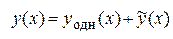 ,
,
где 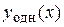 – общее решение соответствующего однородного уравнения, а
– общее решение соответствующего однородного уравнения, а 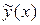 – какое-либо частное решение заданного уравнения.
– какое-либо частное решение заданного уравнения.
1) Найдём решение 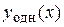 . Для этого составим и решим линейное однородное дифференциальное уравнение, соответствующее данному:
. Для этого составим и решим линейное однородное дифференциальное уравнение, соответствующее данному:
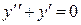 .
.
Характеристическое уравнение  , или
, или  , имеет корни
, имеет корни  ,
, 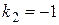 . Поэтому (согласно правилу, сформулированному на странице 53, таблица 3) общее решение имеет вид
. Поэтому (согласно правилу, сформулированному на странице 53, таблица 3) общее решение имеет вид
 , или
, или 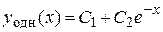 .
.
2) Найдем частное решение 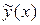 исходного дифференциального уравнения.
исходного дифференциального уравнения.
Функцию 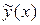 подберем по виду правой части данного дифференциального уравнения и корням соответствующего характеристического уравнения, ориентируясь на таблицу 4.
подберем по виду правой части данного дифференциального уравнения и корням соответствующего характеристического уравнения, ориентируясь на таблицу 4.
Таблица 4
Вид правой части 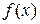
| Корни характеристического уравнения | Вид частного решения 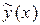
|
I. 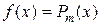 , ,
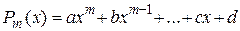 – многочлен степени т,
а, b,…, c, d – известные числа
– многочлен степени т,
а, b,…, c, d – известные числа
| а) Число 0 неявляется корнем характеристического уравнения | 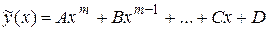 . .
|
| б) Число 0 – корень характеристического уравнения кратности r | 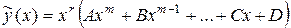
| |
II. 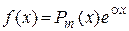 , ,
 – многочлен степени т,
α, а, b,…, c, d – известные числа. – многочлен степени т,
α, а, b,…, c, d – известные числа.
| а) Число aне является корнем характеристического уравнения | 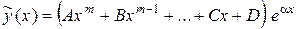 . .
|
| б) Число a – кореньхарактеристического уравнения кратности r |  . .
| |
III. 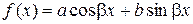 ,
а, b, β– известные числа. ,
а, b, β– известные числа.
| а) Числа  не являются корнями характеристического уравнения, не являются корнями характеристического уравнения,
| 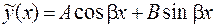 . .
|
б) Числа  – корни характеристического уравнения кратности r – корни характеристического уравнения кратности r
|  . .
| |
IV. 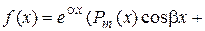
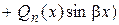 Рт (х) и Q п (x) – многочлены степени т и п соответственно
Рт (х) и Q п (x) – многочлены степени т и п соответственно
| а) Числа 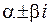 не являются корнями характеристического уравнения не являются корнями характеристического уравнения
| 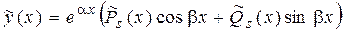 , ,
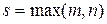 . .
|
б) Числа 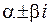 – корнихарактеристического уравнения кратности r – корнихарактеристического уравнения кратности r
| 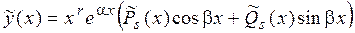 , ,
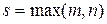 . .
| |
Здесь А, В, С, D – неизвестные буквенные коэффициенты, 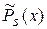 , , 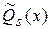 – многочлены степени s с буквенными коэффициентами. – многочлены степени s с буквенными коэффициентами.
|
Правая часть уравнения – функция 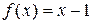 – есть функция вида
– есть функция вида  , где
, где  – многочлен первой степени. Так как число
– многочлен первой степени. Так как число  является корнем характеристического уравнения кратности
является корнем характеристического уравнения кратности 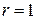 , то имеем случай I,б) таблицы 4. Значит, частное решение будем искать в виде
, то имеем случай I,б) таблицы 4. Значит, частное решение будем искать в виде
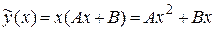 .
.
Неопределенные коэффициенты А и В найдем из условия, что функция 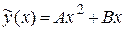 является решением заданного уравнения, а значит, при подстановке этой функции в уравнение оно обращается в верное равенство.
является решением заданного уравнения, а значит, при подстановке этой функции в уравнение оно обращается в верное равенство.
Найдем 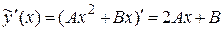 ,
, 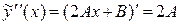 и подставим эти производные в уравнение
и подставим эти производные в уравнение  . Имеем
. Имеем
 ,
, 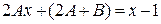 .
.
Получили равенство многочленов. Приравнивая коэффициенты при х, имеем 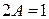 ; приравнивая свободные члены, имеем
; приравнивая свободные члены, имеем  . Таким образом, получили систему уравнений относительно А и B:
. Таким образом, получили систему уравнений относительно А и B:

Решая эту систему, находим 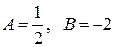 .
.
Значит, частное решение  .
.
3) Запишем общее решение исходного дифференциального уравнения
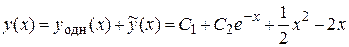 .
.
Ответ: 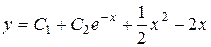 .
.
Пример 7 Решить дифференциальное уравнение  .
.
Решение
Решение данного линейного неоднородного дифференциального уравнения также ищем в виде 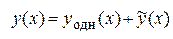 .
.
1) Найдём 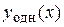 . Для этого составим и решим однородное уравнение, соответствующее данному:
. Для этого составим и решим однородное уравнение, соответствующее данному:
 .
.
Характеристическое уравнение  имеет корни
имеет корни 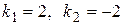 . Поэтому (согласно правилу на странице 53, таблица 3) общее решение однородного уравнения имеет вид
. Поэтому (согласно правилу на странице 53, таблица 3) общее решение однородного уравнения имеет вид
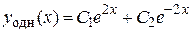 .
.
2) Найдем частное решение 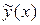 заданного уравнения. Функцию
заданного уравнения. Функцию 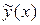 подберем по виду правой части
подберем по виду правой части  и корням характеристического уравнения.
и корням характеристического уравнения.
Правая часть дифференциального уравнения 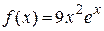 есть функция вида
есть функция вида 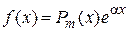 , где
, где 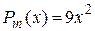 – многочлен второй степени, а
– многочлен второй степени, а  , причем a не является корнем характеристического уравнения. Значит, эта функция относится к типу II,а) таблицы 4, поэтому частное решение уравнения будем искать в виде
, причем a не является корнем характеристического уравнения. Значит, эта функция относится к типу II,а) таблицы 4, поэтому частное решение уравнения будем искать в виде
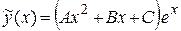 ,
,
где А, В, С – неопределенные коэффициенты.
Найдем эти коэффициенты из условия, что функция 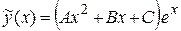 удовлетворяет заданному уравнению. Для этого найдем производные:
удовлетворяет заданному уравнению. Для этого найдем производные:
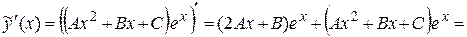
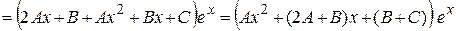 ,
,
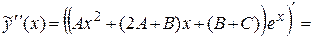
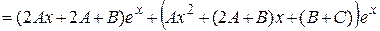 .
.
Подставим в исходное дифференциальное уравнение  вместо у выражение
вместо у выражение 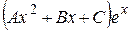 , а вместо у ¢¢ – выражение
, а вместо у ¢¢ – выражение 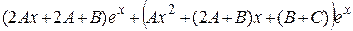 , получим
, получим
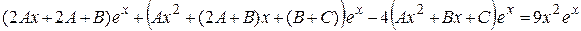 .
.
Разделим обе части этого равенства на 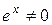 , получим
, получим
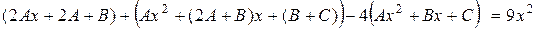 .
.
Раскроем скобки и приведем подобные в левой части равенства
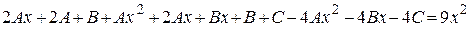 ,
,
в результате имеем
 .
.
Получили равенство двух многочленов. Приравнивая коэффициенты при одинаковых степенях х многочленов в левой и правой частях равенства, получим систему относительно А, В, С:
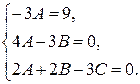
Решая эту систему, находим 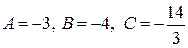 .
.
Значит, частное решение имеет вид 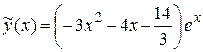 .
.
3) Тогда общее решение заданного дифференциального уравнения
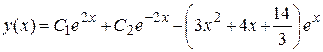 .
.
Ответ: 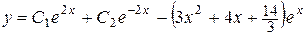
Пример 3. 8 Решить дифференциальное уравнение
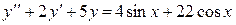 ,
, 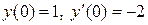 .
.
Решение
Как известно, чтобы найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям, нужно, прежде всего, найти общее решение этого уравнения. Как и в предыдущих примерах, общее решение ищем в виде 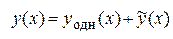 .
.
1) Составим и решим линейное однородное дифференциальное уравнение, соответствующее данному: 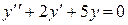 .
.
Имеем: 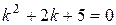 Þ
Þ 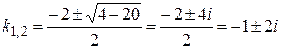 .
.
Тогда 
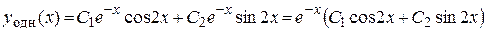 .
.
2) Найдем частное решение 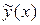 . Правая часть дифференциального уравнения
. Правая часть дифференциального уравнения  относится к виду III,a) таблицы 4:
относится к виду III,a) таблицы 4:
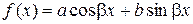 ,
,
где  ,
,  ,
,  , и числа
, и числа  не являются корнями характеристического уравнения. Следовательно, решение
не являются корнями характеристического уравнения. Следовательно, решение 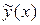 нужно искать в виде
нужно искать в виде
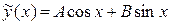
Определим коэффициенты А и В. Для этого находим
 ,
,
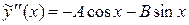 ,
,
и подставив эти соотношения в исходное дифференциальное уравнение, получим
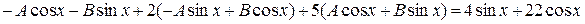 ,
,
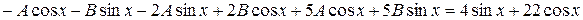 ,
,
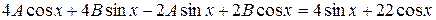 ,
,
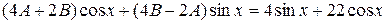 .
.
Приравнивая коэффициенты при 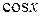 в левой и правой частях этого равенства, имеем
в левой и правой частях этого равенства, имеем 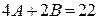 ; приравнивая коэффициенты при
; приравнивая коэффициенты при 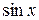 , имеем
, имеем 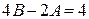 . В результате получим систему уравнений относительно А и В:
. В результате получим систему уравнений относительно А и В:

Решая эту систему, найдем 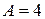 ,
,  . Тогда
. Тогда
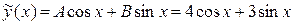 .
.
3) Следовательно, общее решение заданного дифференциального уравнения имеет вид
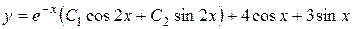 .
.
По условию, требуется найти частное решение заданного дифференциального уравнения, удовлетворяющее начальным условиям 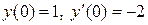 , а это значит: нужно найти такие значения постоянных
, а это значит: нужно найти такие значения постоянных 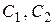 , чтобы найденная функция
, чтобы найденная функция

удовлетворяла этим начальным условиям.
Для этого найдем производную

 .
.
Вычислим 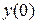 и
и 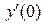 :
:
 ,
,
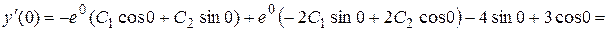
 .
.
Подставим эти значения в равенства 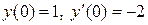 , получим
, получим
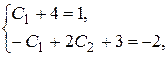 или
или 
Получили систему уравнений относительно 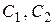 . Решая эту систему, находим
. Решая эту систему, находим 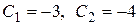 . Тогда искомое частное решение заданного дифференциального уравнения имеет вид
. Тогда искомое частное решение заданного дифференциального уравнения имеет вид
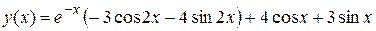 .
.
Ответ: 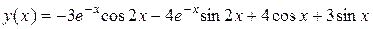 .
.
В некоторых случаях функция  в правой части линейного неоднородного дифференциального уравнения не является функцией «специального вида», но может быть представлена в виде суммы таких функций. Тогда для отыскания частного решения
в правой части линейного неоднородного дифференциального уравнения не является функцией «специального вида», но может быть представлена в виде суммы таких функций. Тогда для отыскания частного решения 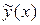 дифференциального уравнения можно использовать «принцип наложения », который заключается в следующем:
дифференциального уравнения можно использовать «принцип наложения », который заключается в следующем:
 Если в уравнении
Если в уравнении  правая часть представляет собой сумму двух функций
правая часть представляет собой сумму двух функций 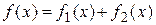 , а
, а 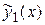 и
и 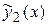 – частные решения уравнений
– частные решения уравнений
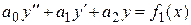 и
и 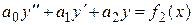
соответственно, то функция  является частным решением исходного уравнения
является частным решением исходного уравнения  .
.
Рассмотрим пример.
Пример 9 Решить уравнение 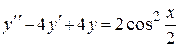 .
.
Решение
1) Найдем общее решение соответствующего однородного дифференциального уравнения:
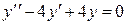 Þ
Þ 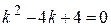 Þ
Þ 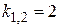 Þ
Þ 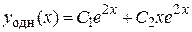 .
.
2) Найдем частное решение 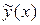 . Правая часть данного линейного неоднородного дифференциального уравнения не является функцией специального вида (смотри таблицу 4). Однако если преобразовать эту функцию:
. Правая часть данного линейного неоднородного дифференциального уравнения не является функцией специального вида (смотри таблицу 4). Однако если преобразовать эту функцию:
 ,
,
то ее можно рассматривать как сумму функций 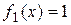 и
и  специального вида. Тогда частное решение исходного дифференциального решение исходного дифференциального уравнения также можно найти методом подбора частного решения, используя принцип наложения. Для этого рассмотрим два дифференциальных уравнения:
специального вида. Тогда частное решение исходного дифференциального решение исходного дифференциального уравнения также можно найти методом подбора частного решения, используя принцип наложения. Для этого рассмотрим два дифференциальных уравнения:
 и
и 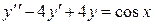
и найдем частное решение каждого из этих уравнений.
а) Для дифференциального уравнения  частное решение будем искать в виде
частное решение будем искать в виде
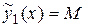 ,
,
так как 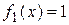 есть многочлен нулевой степени (число), а число
есть многочлен нулевой степени (число), а число  не является корнем характеристического уравнения (случай I,а таблицы 4). Найдем значение параметра М.
не является корнем характеристического уравнения (случай I,а таблицы 4). Найдем значение параметра М.
Имеем:
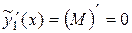 ,
, 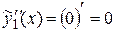 .
.
Подставим 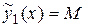 ,
, 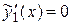 ,
, 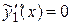 в дифференциальное уравнение
в дифференциальное уравнение  :
:
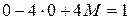 Þ
Þ 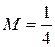 .
.
Тогда  .
.
б) Частное решение 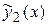 уравнения
уравнения 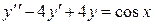 будем искать в виде
будем искать в виде
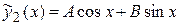 ,
,
так как  есть функция вида
есть функция вида 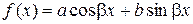 , где
, где 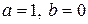 , а характеристическое уравнение не имеет комплексных корней (случай III,а таблицы 4).
, а характеристическое уравнение не имеет комплексных корней (случай III,а таблицы 4).
Для определения коэффициентов А и В находим
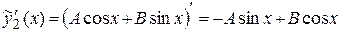 ,
,
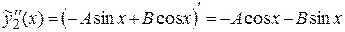 .
.
Подставляя эти производные и функцию 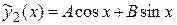 в дифференциальное уравнение
в дифференциальное уравнение 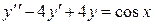 , получим
, получим
 ,
,
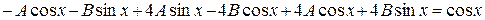 ,
,
 .
.
Приравнивая коэффициенты при одноименных функциях, получим систему уравнений относительно А и В:
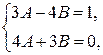
откуда находим 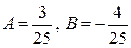 . Тогда
. Тогда  .
.
Следовательно, частное решение исходного дифференциального уравнения имеет вид
 ,
,
а искомое общее решение –
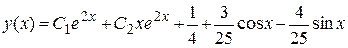 .
.
Ответ: 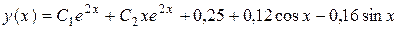 .
.
*) Напомним, что корни квадратного уравнения находят по формуле, где.
*) Количество линейно независимых функций ФСР равно порядку дифференциального уравнения