Типовая структура АСНИ и требования к ее компонентам.

Симплекс-метод решения задачи ЛП

Схемы программ. Способы представления схемы программы.

4.Решить графически задачу линейного программирования. Провести анализ полученных решений.

F(x)=-x1→extr

x1+x2≤1 x1≥0

x2≥0 ____________________________________________________________________________

Типовая структура АСНИ и требования к ее компонентам.

Основными структурными звеньями АСНИ являются подсистемы. Подсистемой АСНИ называется выделенная по некоторым признакам часть АСНИ, обеспечивающая выполнение определенных автоматизированных процедур исследований (испытаний) и получение соответствующих выходных документов.

Различаются объектно-ориентированные (объектные) и обслуживающие подсистемы АСНИ.

Объектная подсистема осуществляет получение и обработку экспериментальных данных с некоторого объекта.

Объектными могут быть, например, подсистемы:

• · обработки экспериментальных данных, получаемых со специализированных установок

(ускорителей, спектрометров, испытательных стендов);

• · обработки данных на морских судах, системы для сейсморазведки и т.п.;
• · коллективного пользования для куста однородных экспериментальных установок или

стендов.
Обслуживающая подсистема осуществляет функции управления и обработки информации, не

зависящие от особенностей исследуемого явления, объекта или процесса. Обслуживающими могут быть, например, подсистемы:

• · управления АСНИ;
• · диалоговых процедур;

• · численного анализа;
• · планирования и оптимизации эксперимента;
• · ввода, обработки и вывода графической информации;
• · информационно-поисковых процедур.

При создании или заимствовании компонентов АСНИ должны обеспечиваться требования к этим компонентам, вытекающие из общесистемных принципов:

• · последовательное расширение сферы автоматизации научных исследований;
• · интеграция АСНИ;
• · типизация, унификация и стандартизация компонентов АСНИ;
• · тиражирование типовых подсистем и компонентов АСНИ;
• · применение единой методологии создания и развития АСНИ и т.д. 2.Симплекс-метод решения задачи ЛП (линейного программирования)

Движение к точке оптимума осуществляется путем перехода от одной угловой точки к соседней, которая ближе и быстрее приближает к Xопт. Такую схему перебора точек, называемую симплекс- метод, предложил Р. Данцигом.

Угловые точки характеризуются m базисными переменными, поэтому переход от одной угловой точки к соседней возможно осуществить сменой в базисе только одной базисной переменной на переменную из не базиса.

Реализация симплекс-метода в силу различных особенностей и постановок задач ЛП имеет различные модификации (базовая форма, симплексная таблица, модифицированный симплекс-метод).

Построение симплекс-таблиц продолжается до тех пор, пока не будет получено оптимальное решение. Определение оптимального решения задачи линейного программирования с помощью симплекс-таблицы производится следующим образом:

Если последняя строка (значения целевой функции) не содержит отрицательных элементов, следовательно, найдет оптимальный план.

Данный метод является методом целенаправленного перебора опорных решений задачи линейного программирования. Он позволяет за конечное число шагов либо найти оптимальное решение, либо установить, что оптимальное решение отсутствует.

Основное содержание симплексного метода заключается в следующем:

• · Указать способ нахождения оптимального опорного решения
• · Указать способ перехода от одного опорного решения к другому, на котором значение

целевой функции будет ближе к оптимальному, т.е. указать способ улучшения опорного решения

· Задать критерии, которые позволяют своевременно прекратить перебор опорных решений

на оптимальном решении или следать заключение об отсутствии оптимального решения. Алгоритм симплексного метода решения задач линейного программирования

Для того, чтобы решить задачу симплексным методом необходимо выполнить следующее:
· Привести задачу к каноническому виду
· Найти начальное опорное решение с "единичным базисом" (если опорное решение

отсутствует, то задача не имеет решение ввиду несовместимости системы ограничений)
· Вычислить оценки разложений векторов по базису опорного решения и заполнить таблицу

симплексного метода
· Если выполняется признак единственности оптимального решения, то решение задачи

заканчивается
· Если выполняется условие существования множества оптимальных решений, то путем

простого перебора находят все оптимальные решения

3. UML-метод моделирования разрабатываемой программной системы. Диаграмма классов.

UML (United Modeling Language) - унифицированный язык моделирования является результатом совместной разработки специалистов программной инженерии и инженерии требований. Он широко используется ведущими разработчиками ПО как метод моделирования на этапах ЖЦ разработки ПС.

В основу метода положена парадигма объектного подхода, при котором концептуальное моделирование проблемы происходит в терминах взаимодействия объектов и включает:

· онтологию домена, которая определяет состав классов объектов домена, их атрибутов и взаимоотношений, а также услуг (операций), которые могут выполнять объекты классов;

· модель поведения задает возможные состояния объектов, инцидентов, инициирующих переходы с одного состояния к другому, а также сообщения, которыми обмениваются объекты;

· модель процессов определяет действия, которые выполняются при проектировании объектов, как компонентов.

Модель требований в UML - это совокупность диаграмм, которые визуализируют основные элементы структуры системы.

Диаграмма классов отображает онтологию домена, эквивалентна структуре информационной модели метода С.Шлеера и С.Меллора, определяет состав классов объектов и их взаимоотношений. Диаграмма задается иконами, как визуальное изображение понятий, и связей между ними. Верхняя часть иконы - обязательная, она определяет имя класса. Вторая и третья части иконы определяют соответственно список атрибутов класса и список операций класса.

Пользователь может определять специфические для него атрибуты. Под операцией понимается сервис, который экземпляр класса может выполнять, если к нему будет произведен соответствующий вызов. Операция имеет название и список аргументов.

Классы могут находиться в следующих отношениях или связях.

Ассоциация - взаимная зависимость между объектами разных классов, каждый из которых является равноправным ее членом. Она может обозначать количество экземпляров объектов каждого класса, которые принимают участие в связи (0 - если ни одного, 1 - если один, N - если много).

Пусть на отрезке существует единственный корень уравнения:

,

а 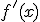существует, непрерывна и отлична от нуля на . Перепишем следующим образом:

и применим к этому выражению формулу Лагранжа:

Заменим на , а - на и получим формулу итерационного процесса:

Выразим отсюда :

Метод касательных имеет (когда сходится) квадратичную скорость сходимости:

Зависимость между классами, при которой класс-клиент может использовать

определенную операцию другого класса; классы могут быть связаны отношением трассирования, если один класс трансформируется в другой в результате выполнения определенного процесса ЖЦ.

Экземпляризация - зависимость между параметризированным абстрактным классом- шаблоном (template) и реальным классом, который инициирует параметры шаблона (например, контейнерные классы языка С++).

 

4.Решить графически задачу линейного программирования. Провести анализ полученных решений.

ограничений:

F(x)=-x1→extr

x1+x2≤1 x1≥0

x2≥0

Необходимо найти минимальное значение целевой функции F = -x1 → extr, при системе

x1+x2≤1, (1)

x1 ≥ 0, (2) x2 ≥ 0, (3)

Задача относится к ЗЛП, следовательно, искомое решение находится на границе ОДЗ: в вершине

или на ребре.

Шаг No1. Построим область допустимых решений, т.е. решим графически систему неравенств.

Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами

(полуплоскости обозначены штрихом).

Шаг No2.

x1+x2 ≤1 Построим прямую: x1 + x2 = 1

Пусть x1 =0 => x2 = 1
Пусть x2 =0 => x1 = 1
Найдены координаты двух точек (0, 1) и (1,0). Соединяем их и получаем необходимую прямую (1).

Пересечением полуплоскостей будет являться область, координаты точек которого являются

ОДЗ для данной задачи.

Шаг No3. Рассмотрим целевую функцию задачи F = -x1 → extr (min, max). Данная задача является

обратной (противоположной) задаче F = x1 → extr (max, min).

Построим прямую, отвечающую значению функции F = 0: F = -x1 = 0. Вектор-градиент,

составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (-1; 0). Будем двигать эту прямую x2=0 параллельным образом. Поскольку нас интересует минимальное и максимальное значение целевой функции, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной

линией.

Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате

пересечения прямых (2) и (1), то ее координаты удовлетворяют уравнениям этих прямых:

Функция F достигает наименьшего значения в точке C. (см. рисунок справа) Координаты точки C (1,0) известны.

Вычислим значение функции F в точке C (1,0)., теперь найдём минимальное значение целевой̆ функции:

extr1 (F(X)) = -1*1 + 0*0 = -1

Ответ:

x2=0; x1+x2=1

Решив систему уравнений, получим: x1 = 1, x2 = 0

Максимальное значение целевой функции: extr2(F(X)) = 0*0 = 0

x1 = 1 x2 = 0

F min = -1

F max = 0