ПРАКТИЧЕСКАЯ РАБОТА №1
Вычисление производных.
Цель: - повторить правила и формулы вычисления производных;
- закрепить навыки вычисления производных.
Теоретический материал.
Пусть величина у зависит от аргумента х как у = f(x). Если f(x) была зафиксирована в двух точках значениях аргумента: x1, x2, то мы получаем величины у1 = f(x1), и у2 = f(x2). Разность двух значений аргумента x 2, x 1 назовём приращением аргумента и обозначим как Δ x = x 2- x 1. Если аргумент изменился на Δ x = x 2- x 1, то функция изменилась (приросла) как разность двух значений функции
у1 = f(x1), у 2 = f(x2) на величину приращения функции Δf. Записывается обычно так:
Δ f = у1 – у2 = f(x2 ) - f(x1). Считается, что если величины x2 и x1, бесконечно близки по величине друг к другу, тогда Δ x = x2 – x 1, - бесконечно мало.
Производной функции f(x) в точке x 0 называется предел отношения приращения функции Δ f в этой точке к приращению аргумента Δ х, когда последнее стремится к нулю (бесконечно мало). 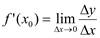
Нахождение производной называется дифференцированием. Функция f, имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой на данном промежутке.
Правила дифференцирования (и, v, w — функции аргумента х, по которому
производится дифференцирование, с - постоянная).
1. Производная алгебраической суммы 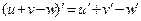
2. Производная произведения 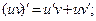
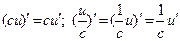
3. Производная частного (дроби) 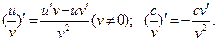
4. Производная сложной функции (функции от функции).
Если 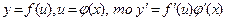
Таблица основных формул дифференцирования
| № п/п | Функция | Производная | № п/п | Функция | Производная | № п/п | Функция | Производная |
| C (постоянная) | ex | ex | ctg x | 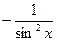
| ||||
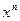 (n – постоянная) (n – постоянная)
| 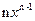
| 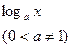
| 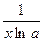
| arcsin x | 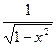
| |||
| x | ln x | 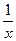
| arccos x | 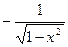
| ||||
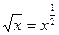
| 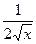
| sin x | cos x | arctg x | 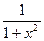
| |||
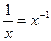
| 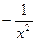
| cos x | –sin x | arcctg x | 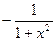
| |||
| ax, (a > 0) | ax ln a | tg x |  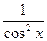
| lg x | 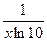
|
Порядок выполнения работы.
1)Изучите примеры нахождения производных.
Пример 1. Найдите производную функции:
1) 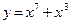 ; 2)
; 2) 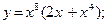 3)
3) 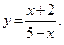
Решение
1) 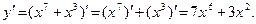 2)
2) 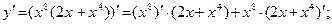 Учитывая, что
Учитывая, что 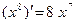 ; ; 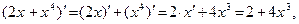 имеем имеем
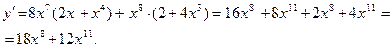 3) 3) 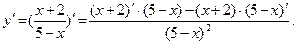 Учитывая, что
Учитывая, что 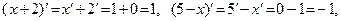 имеем имеем
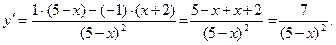
| Пояснения
В задании 1 надо найти производную суммы по формуле 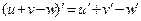 ;
в задании 2 – производную произведения ;
в задании 2 – производную произведения 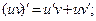 в задании 3 – производную частного в задании 3 – производную частного 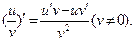 Также в заданиях 1 и 2 следует использовать формулу
Также в заданиях 1 и 2 следует использовать формулу 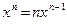 , а в задании 2 учесть, что при вычислении производной 2 x постоянный множитель 2
можно вынести за знак производной. , а в задании 2 учесть, что при вычислении производной 2 x постоянный множитель 2
можно вынести за знак производной.
|
Пример 2. Вычислите значение производной функции 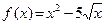 в точках х = 4 и х = 0,01.
в точках х = 4 и х = 0,01.
Решение
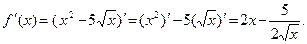
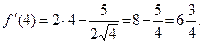
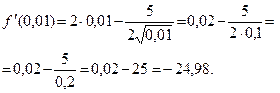
| Пояснения
Для нахождения производной в указанных точках достаточно найти производную данной функции и в полученное выражение подставить заданные значения аргумента. При вычислении производной следует учесть, что заданную разность можно рассматривать, как алгебраическую сумму выражений х 2 и 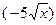 , а при нахождении производной , а при нахождении производной 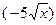 за знак производной вынести постоянный множитель (- 5). за знак производной вынести постоянный множитель (- 5).
|
Пример 3. Найдите значения х, при которых производная функции 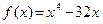 равна 0.
равна 0.
Решение
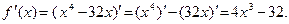
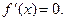 Тогда Тогда 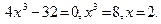 Ответ: х = 2.
Ответ: х = 2.
| Пояснения Чтобы найти соответствующие значения х, достаточно найти производную данной функции, приравнять её к нулю и решить полученное уравнение. |
Пример 4. Найдите производную функции:
1) 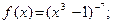 2)
2) 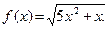
Решение
1) 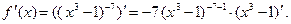 Учитывая, что
Учитывая, что 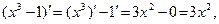 получаем получаем 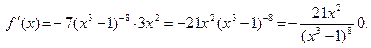
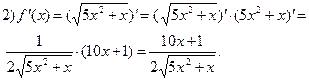
| Пояснения В заданиях 1 и 2 необходимо найти соответственно производную степени и корня, но в основании степени и под знаком корня стоит не аргумент х, а выражение с этим аргументом (тоже функция от х). Следовательно, необходимо найти производные сложных функций. |
2) Выполните задания.
1 вариант
Уровень.
1) Найти соответствие между функцией и её производной.
| 1. С | 2.
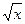
| 3. х | 4.
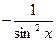
| 5.
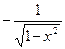
| 6.
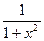
|
7.
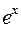
| 8.
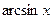
| 9.
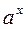
| 10.
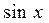
| 11.
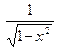
| 12.
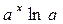
|
13.
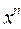
| 14.
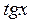
| 15.
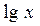
| 16.
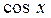
| 17.
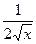
| 18.
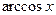
|
| 19. | 20.
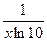
| 21.
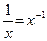
| 22.
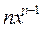
| 23.
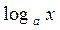
| 24.
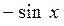
|
25.
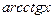
| 26.
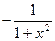
| 27. | 28.
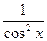
| 29.
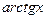
| 30.
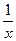
|
31.
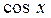
| 32.
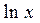
| 33.
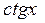
| 34.
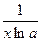
| 35.
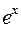
| 36.
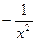
|
2) Сопоставьте функции её производную.
| Функция | Производная | |||
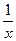
| 2 х | -2 cos x sin x | cos(x +2) | |
| x 2 + 1 | ||||
| sin(x + 2) | ||||
| ln x | ||||
| cos2 x |
Уровень.
3) Вычислите производную функции:
1) у = 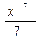 ; а) х 6; б)
; а) х 6; б) 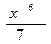 ; в) 7 х 7.
; в) 7 х 7.
2) у = х 3 + 5 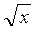 ; а) 4 х 2 +5
; а) 4 х 2 +5 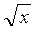 ; б) 3 x 2 +
; б) 3 x 2 + 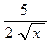 ; в) 3 х 2 +
; в) 3 х 2 + 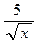 .
.
3) у = 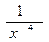 ; а) х - 4; б)
; а) х - 4; б) 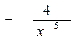 ; в)
; в) 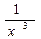 .
.
4) у = 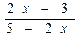 ; а)
; а) 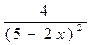 ; б) -
; б) - 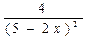 ; в)
; в) 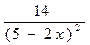 .
.
4) Вычислите значение производной функции у = 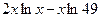 при х = 7.
при х = 7.
| а | б | в | г |
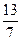
| 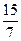
|
Уровень.
5) Вычислите производную сложной функции f(x) = 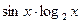 .
.
2 вариант
Уровень.
1) Найти соответствие между функцией и её производной.
| 1. С | 2.
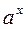
| 3. х | 4.
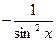
| 5.
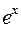
| 6.
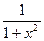
|
7.
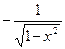
| 8.
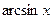
| 9.
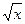
| 10.
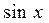
| 11. | 12.
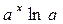
|
13.
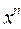
| 14.
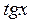
| 15.
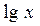
| 16.
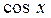
| 17.
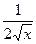
| 18.
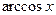
|
| 19. | 20.
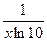
| 21.
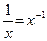
| 22.
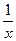
| 23.
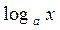
| 24.
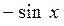
|
25.
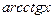
| 26.
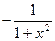
| 27.
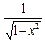
| 28.
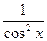
| 29.
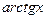
| 30.
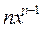
|
31.
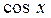
| 32.
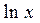
| 33.
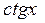
| 34.
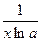
| 35.
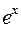
| 36.
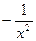
|
2) Сопоставьте функции её производную
| Функция | Производная | |||
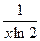
| 5 х 4 | 2 cos x sin x | - sin (x - 6) | |
| x 5 + 1 | ||||
| cos(x -6) | ||||
| log 2 x | ||||
| sin2 x |
Уровень.
3) Вычислите производную функции:
1) у = 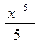 ; а) х 4; б)
; а) х 4; б) 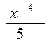 ; в) 5 х 5.
; в) 5 х 5.
2) у = х 7 + 3 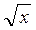 ; а) 7 х 6 +3
; а) 7 х 6 +3 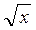 ;б) 7 x 6 +
;б) 7 x 6 + 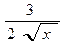 ; в) 7 х 6 +
; в) 7 х 6 + 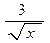 .
.
3) у = 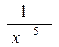 ; а) х - 5; б)
; а) х - 5; б) 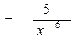 ; в)
; в) 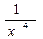 .
.
4) у = 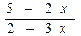 ; а)
; а) 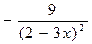 ; б)
; б) 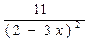 ; в)
; в) 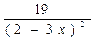 .
.
4) Вычислите значение производной функции у = 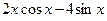 при х = 0.
при х = 0.
| а | б | в | г |
| 1,5 | -2 |
Уровень.
5) Вычислите производную сложной функции f(x) = 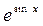 .
.