Законы сохранения в механике

Работа и энергия

Работой A, совершенной постоянной силой 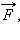называется скалярное произведение векторов силы и перемещения:

где α – угол между векторами силы и перемещения. Единицей работы в системе СИ является джоуль (Дж).

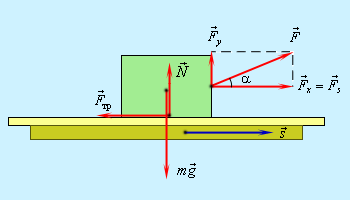
Рис. 1. Работа силы F

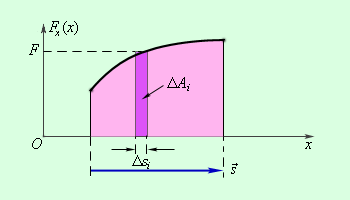
Если к телу приложено несколько сил, то общая работа равна алгебраической сумме работ, совершаемых отдельными силами, и при поступательном движении тела равна работе равнодействующей силы. Работа переменной силы может быть найдена графически.

Рис. 2. Работа переменной силы F.

Мощность N – это отношение работы Δ A к промежутку времени Δ t, в течение которого она совершается:

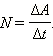
В системе СИ единица мощности называется ватт (Вт).

 

Вид энергии, определяющейся взаимным расположением тел, называется потенциальной энергией. Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положением. Такие силы называются консервативными, к ним относятся, например, сила тяжести и сила Кулона.

Рис. 3. Работа консервативных сил по замкнутой траектории равна нулю

Потенциальная энергия определяется с точностью до константы. Физический смысл имеет изменение потенциальной энергии.

Теорема о потенциальной энергии. Работа, совершаемая консервативными силами, равна изменению потенциальной энергии тела, взятому с противоположным знаком:

A = – (E p2 – E p1).

Потенциальная энергия тела в поле тяжести равна:

E p = mgh.

Потенциальная энергия деформированной пружины равна:

Кинетическая энергия – это энергия, которой обладают тела вследствие своего движения:

Теорема о кинетической энергии. Работа равнодействующей всех сил, приложенных к телу, равна изменению его кинетической энергии:

A = E k2 – E k1.

Силы в механике

Закон всемирного тяготения. Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния r между ними:

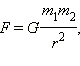
где G = 6,67∙10^–11 м³/кг∙с² (СИ) – гравитационная постоянная.

Закон всемирного тяготения справедлив для точечных, а также сферически симметричных тел. Приближенно он выполняется для любых тел, если расстояние между ними значительно больше их размеров.

Рис. 1. Закон всемирного тяготения

Одним из проявлений закона всемирного тяготения является сила тяжести. На поверхности Земли поэтому сила всемирного тяготения, действующая на тело массой m, равна:

где ускорение свободного падения Здесь масса Земли равна а ее радиус Вблизи поверхности Земли ускорение свободного падения равно приблизительно g = 9,8 м/с².

Сила F называется силой тяжести и направлена к центру Земли.

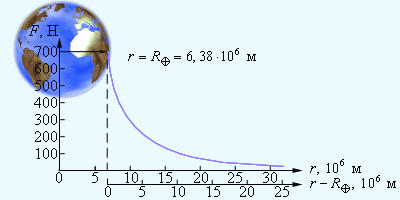
Рис. 2. Сила тяжести на различных расстояниях от Земли. При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Масса тела принята равной m = 70 кг

В современной физике считается, что гравитационное притяжение обусловлено наличием гравитационного поля, посредством которого тела действуют друг на друга.

Сила, с которой тело действует на неподвижную горизонтальную опору или подвес, называется весом тела По третьему закону Ньютона, с той же по модулю силой опора или подвес действуют на тело; эта сила называется реакцией опоры Понятие веса может быть распространено и на случай, когда опора или подвес движутся с ускорением относительно инерциальных систем.

Если опора или подвес двигается с некоторым ускорением, то сила давления со стороны тела (то есть вес тела) изменяется.

В частности, если опора движется с ускорением направленным против силы тяжести, то вес тела обращается в нуль. Такое состояние называют невесомостью. Состояние невесомости испытывает космонавт в космическом корабле.

Рис. 3. Вес тела и реакция опоры

Изменение формы или размеров тела называется деформацией. Деформации бывают упругими и пластичными. При упругих деформациях тело восстанавливает свою форму и размеры после прекращения действия силы, при пластичных – нет. При упругих деформациях справедлив закон Гука: деформация пропорциональна вызывающей ее силе.

F внеш = – F упр = kx.

Коэффициент k называется жесткостью. Знак минус показывает, что упругая сила всегда направлена в сторону, противоположную деформации.

Рис. 4. Сила упругости

При больших силах деформация становится пластической, график зависимости силы упругости от удлинения становится нелинейным, и закон Гука перестает действовать.

Рис. 5. Зависимость модуля силы упругости от удлинения

Силы, действующие между поверхностями соприкасающихся твердых тел, называются силами сухого трения. Они всегда направлены по касательной к соприкасающимся поверхностям и подразделяются на силы трения покоя, скольжения и качения.

Рис. 6. Сила трения покоя

Сила трения покоя – величина непостоянная, она может изменятся от нуля до некоторого максимального значения F _{тр max}. Сила трения покоя равна по модулю и противоположна по направлению проекции внешней силы, направленной параллельно поверхности соприкосновения неподвижных относительно друг друга тел.

Если проекция внешней силы больше F _{тр max}, то возникает движение. Силу трения в этом случае называют силой трения скольжения. Экспериментально доказано, что сила трения скольжения пропорциональна силе реакции опоры:

F тр max = μ N.

Коэффициент трения μ зависит от материалов, из которых изготовлены соприкасающиеся тела, и не зависит от размеров соприкасающихся поверхностей.

Сила трения скольжения всегда направлена против относительного движения тела.

Сила трения качения возникает, если тело катится по поверхности. Она значительно меньше силы трения скольжения для тела соответствующей массы. При решении многих физических задач силой трения качения можно пренебречь.

При движении в жидкости или газе возникает сила вязкого трения. При вязком трении нет трения покоя. Сила вязкого трения направлена в сторону, противоположную скорости тела. Зависимость от модуля скорости может быть линейной F = –βυили квадратичной F = –αυ².

Статика

Для того, чтобы материальная точка находилась в равновесии, то есть в состоянии покоя относительно других тел, неподвижных в рассматриваемой системе отсчета, необходимо, чтобы равнодействующая всех сил, приложенных к ней, равнялась нулю:

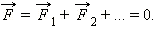
Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил. Должна быть равна нулю сумма моментов всех сил относительно этой оси:

Момент силы – это произведение модуля силы на плечо d:

M = F · d.

Плечо – это длина перпендикуляра, проведенного к оси вращения от линии действия силы.

Рис. 1. К определению момента силы

Оба приведенных условия являются недостаточными для того, чтобы тело находилось в покое. Даже при их соблюдении тело может равномерно вращаться или двигаться поступательно с постоянной скоростью.

 

В механике различают три вида равновесия. При устойчивом равновесии малые отклонения тела от этого состояния вызывают силы или моменты сил, стремящиеся возвратить тело в равновесное состояние. При неустойчивом равновесии силы или моменты сил удаляют тело от положения равновесия. Наконец, если тело находится в безразличном состоянии равновесия, то при отклонении тела от состояния равновесия сил (или моментов сил) не возникает.

Для системы из многих частиц радиус-вектор 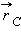центра масс определяется выражением:

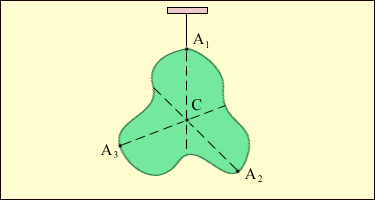
Для сплошного тела суммы в выражении для заменяются интегралами. Легко видеть, что в однородном поле тяготения центр масс совпадает с центром тяжести. Поэтому положение центра масс тела сложной формы можно практически определить путем последовательного подвешивания его за несколько точек и отмечая по отвесу вертикальные линии (рис. 2).

Рис. 2. Определение положения центра масс C тела сложной формы. A 1, A 2, A 3 точки подвеса.

 

Законы сохранения в механике

Импульсом тела называют векторную величину, равную произведению массы тела на его скорость:

Импульсом силы называют произведение силы на время ее действия 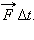Изменение импульса тела равно произведению силы на время ее действия 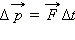или

Эта формула выражает второй закон Ньютона в импульсном представлении.

Закон сохранения импульса. В замкнутой системе, в которой на тела действуют только внутренние силы, векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой:

 

Рис. 1. Закон сохранения импульса на примере столкновения шаров

Импульс может сохраняться и в незамкнутой системе. Это происходит в том случае, если равнодействующая всех внешних сил равна нулю, либо время действия этих сил пренебрежимо мало.

 

Закон сохранения импульса можно применить к реактивному движению – движению тела, возникающему в результате выброса им вещества. В применении к движению ракеты ее скорость υ после истечения газов равна:

где u – скорость газов относительно ракеты, M ₀ – начальная масса ракеты, а M – полезная масса ракеты. Это соотношение называется формулой Циолковского.

Ракета является примером тела переменной массы. К таким телам можно применять второй закон Ньютона, но ко всем внешним силам, действующим на тело переменной массы, следует добавлять силу реакции вытекающей струи:

Здесь 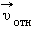– скорость истекающих газов относительно ракеты, μ – масса вещества, истекающего за 1 с. В случае ракеты μ – расход топлива за 1 с:

Абсолютно упругим ударом называется столкновение двух тел, в результате которого сохраняется механическая энергия системы тел:

Если же удар неупругий, то механическая энергия полностью или частично переходит во внутреннюю энергию сталкивающихся тел. В обоих случаях выполняется закон сохранения импульса.

 

Если в системе действуют только потенциальные силы, то справедлив закон сохранения механической энергии: в замкнутой системе сумма кинетической и потенциальной энергии тел остается неизменной:

Если же в системе имеются диссипативные силы (силы трения), то часть механической энергии переходит в тепло: