Изучение основного уравнения динамики вращательного движения на маятнике Обербека
Выполнил студент группы 607-61
Исрапов Шамиль
Проверил: Ельников А.В Лебедев С.В
Цель работы: изучение динамики вращательного движения, измерение момента инерции маятника Обербека.
Теоретическая часть
Вращательным движением называется такое движение, при котором все точки твердого тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения. Вращательное движение тела описывают с помощью углового перемещения 
– вектора, численно равного углу поворота тела и направленного вдоль оси вращения так, что если смотреть с его конца, то вращение тела видится происходящим против часовой стрелки. Быстрота изменения вектора углового перемещения характеризуется угловой скоростью 
:
.
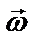В свою очередь, быстрота изменения вектора угловой скорости характеризуется угловым ускорением 
:
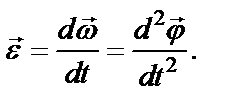
Линейная скорость 
, тангенциальное 
и нормальное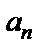 
ускорения любой точки вращающегося твердого тела связаны с характеристиками вращательного движения следующими соотношениями:
, 
, 
,
где: R – расстояние от рассматриваемой точки тела до оси вращения.
Мерой инертности тела при вращательном движении служит момент инерции J. Это скалярная величина, равная сумме произведений масс n материальных точек тела на квадраты их расстояний ri до оси вращения:
.
В случае непрерывного распределения масс эта сумма сводится к интегралу:
,
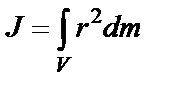где: V – объем тела.
Для описания вращательного движения твердого тела вводят понятие момента силы 
относительно неподвижной точки. Это векторная величина, равная векторному произведению радиус-вектора 
, проведенного из начала координат в точку приложения силы 
, и силы 
:
.
Модуль момента силы
,
где: 
– плечо силы, 
– угол между векторами 
и 
.
Основное уравнение динамики вращательного движения записывается следующим образом:
.
Угловое ускорение, приобретаемое твердым телом, прямо пропорционально результирующему моменту всех действующих на тело внешних сил и обратно пропорционально моменту инерции тела.
Описание экспериментальной установки
Общий вид маятника приведен на рис. 4.2. На вертикальной стойке 2 основания 1 крепятся три кронштейна: верхний 3, средний 4 и кронштейн 5 для установки фотодатчика 6. Основание 1 снабжено тремя регулируемыми опорами 7 и винтом-барашком 8 для фиксации стойки. Вертикальная стойка 2 выполнена из металлической трубы, на которую нанесена миллиметровая шкала, и имеет визир 19. На верхнем кронштейне 3 размещается узел подшипников 9 с малоинерционным шкивом 10 изменения направления движения капроновой нити 11, на которой подвешен наборный груз 12. Верхний кронштейн 3 имеет винт-барашек для крепления на вертикальной стойке 2. На
Расчётные формулы:
В данной работе осуществляется экспериментальная проверка основного уравнения динамики вращательного движения с помощью маятника Обербека. Маятник представляет собой маховик, которому придана крестообразная форма.
По четырем взаимно-перпендикулярным стержням могут перемещаться грузы массой m 0. На общей оси находится шкив, на который наматывается нить с привязанным к ней грузом массой m. Под действием падающего груза нить разматывается и приводит маховик в равноускоренное вращательное движение. При этом угловое ускорение крестовины определяется соотношением:
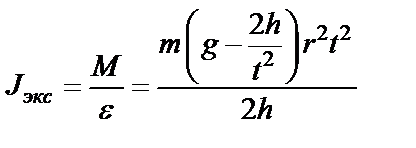-- экспериментальное значение момента инерции маятника.
– момент силы.
-- угловое ускорение крестовины.
а – ускорение падающего груза.
r = d/ 2 – радиус шкива.
h – высота падения груза.
t – время падения груза.
m – масса падающего груза.
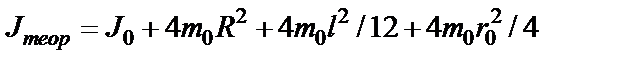-- теоретическое значение момента инерции маятника.
-- Момент инерции системы без грузов.
m 0 = 0,114 кг – масса подвижного груза крестовины.
R – расстояние от центра масс подвижного груза до оси вращения.
r 0= 0,015 м – радиус груза.
l = 0,02 м – длина образующей груза.
l 1 = 0,15 м – длина одного из стержней крестовины.
m 1= 0,023 кг – масса стержня.
Задание 1: определить момент инерции крестовины.
Таблица 1.
| r 1 =0,2м; h =0,75м; g = 9,8 м/ с2. | |||||||
| m 1=0,0589кг. | |||||||
| t, c | 10,43 | 10,21 | 10,31 | 10,52 | 10,35 | t cp, c | 10,364 |
| m 2=0,1148кг. | |||||||
| t, c | 7,38 | 7,49 | 7,53 | 7,42 | 7,44 | t cp, c | 7,452 |
| m 3=0,1706кг. | |||||||
| t, c | 5,59 | 6,16 | 6,05 | 6,16 | 6,10 | t cp, c | 6,012 |
| m 4=0,2263кг. | |||||||
| t, c | 5,29 | 5,37 | 5,50 | 5,37 | 5,41 | t cp, c | 5,388 |
| m 5=0,2763кг. | |||||||
| t, c | 4,64 | 4,62 | 4,54 | 4,73 | 4,51 | t cp, c | 4,622 |
Расчеты по Т1.
∆а1=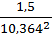 
= 
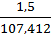=0,014 
∆а2= 
= 
=0,0270
∆а3= 
= 
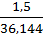=0,0415
∆а4= 
= 
=0,0517
∆а5= 
= 
=0,0702
M1=2*0,0589*(9,8-0,014)=0,1178*9,786=1,153
M2=2*0,1148*(9,8-0,027)=0,2296*9,773=2,244
M3=2*0,1706*(9,8-0,0415)=0,3412*9,7585=3,3296
M4=2*0,2263*(9,8-0,0517)=0,4526*9,7483=4,412
M5=2*0,2763*(9,8-0,0702)=0,5526*9,7298=5,377
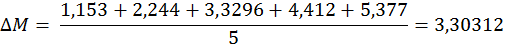
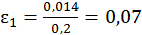
Задание 2: определение зависимости момента инерции J от расстояния грузов до оси вращения крестовины R.
Таблица 2.
| № | r1=0,2м. h=0,75м. m=0.0589кг. | ||||
| R1=0,18м. | R2=0,16м. | R3=0,14м. | R4=0,12м. | R5=0,1м. | |
| t1 | t2 | t3 | t4 | t5 | |
| 9.22 | 8.73 | 7.95 | 7.13 | 6.45 | |
| 9.49 | 8.62 | 7.91 | 7.26 | 6.53 | |
| 9.31 | 8.59 | 7.89 | 7.36 | 6.66 | |
| 9.37 | 8.67 | 8.01 | 7.20 | 6.49 | |
| 9.49 | 8.69 | 8.07 | 7.31 | 6.61 | |
| Ср.зн. | t1=9.376 с | t2=8.66 с | t3=7.966 с | t4=7.257 с | t5=6.548 с |
Расчеты по Т2.
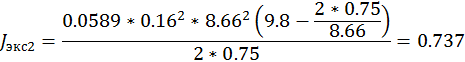
Вывод: В данной работе мы изучили и экспериментально проверили основное уравнение динамики вращательного движения с помощью маятника Обербека