Лабораторная работа № 1. Исследование алгоритмов сжатия информации
Алгоритм Хаффмана
Алгоритм Хаффмана основывается на том, что символы в текстах как правило встречаются с различной частотой.
При обычном кодировании мы каждый символ записываем в фиксированном количестве бит, например каждый символ в одном байте, или в двух.
Однако, т. к. некоторые символы встречаются чаще, а некоторые реже − можно записать часто встречающиеся символы в небольшом количестве бит, а для редко встречающихся символов использовать более длинные коды. Тогда суммарная длина закодированного текста может стать меньше.
Алгоритм Хаффмана на примере
Необходимо закодировать строку "Сжатие Хаффмана"
Вначале нужно подсчитать количество вхождений каждого символа в тексте.
| С | ж | а | т | и | е | Х | ф | м | н | |
Эта таблица называется "таблица частот".
Теперь необходимо построить дерево.
Узел дерева будет образован набором символов и числом - суммарным количеством вхождений данных символов в тексте. Назовем указанное число - весом узла.
Листьями дерева будут узлы, образованные одним символом:

Далее необходимо выполнить следующее:
1) Найти среди узлов, не имеющих родителя, два узла, имеющих в сумме наименьший вес.
2) Создать новый узел, его потомками будут два выбранных узла. Его весом будет сумма весов выбранных улов. Его набор символов будет образован в результате объединения наборов символов выбранных узлов.
Создаем первый узел
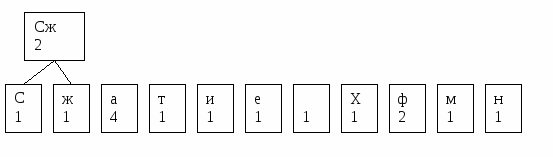
Создаем еще один узел

Создаем еще один узел

Создаем еще один узел

Создаем еще один узел

Создаем еще один узел

Создаем еще один узел

Создаем еще один узел

Создаем еще один узел

Создаем еще один узел

Теперь для каждого узла, имеющего потомков, пометим дуги, идущие вниз, на одной дуге напишем 0, на другой 1.

Чтобы получить код символа, надо, начиная с корня дерева идти вниз до листа соответствующего данному символу. При этом следует записывать те значения, которые написаны на тех дугах, которые мы проходим.
Получаются следующие коды
| С | |
| ж | |
| а | |
| т | |
| и | |
| е | |
| Х | |
| ф | |
| м | |
| н |
Заметим, что код является префиксным, т. е. ни один код символа не является префиксом кода другого символа. Также видно, что для часто встречающихся символов коды короче.
Закодированная строка будет выглядеть:
| С | ж | а | т | и | е | Х | а | ф | ф | м | а | н | а | |
Т. е.
Декодирование
Для декодирования можно воспользоваться построенным деревом. Начинаем с корня дерева и в качестве текущего бита берем начало текста.
В цикле делаем следующее
1) Смотрим, какое значение у текущего бита, и идем вниз по дереву по дуге, на которой указано такое же значение.
2) Переходим к следующему биту.
3) Если сейчас находимся в листе дерева: читаем символ находящийся в этом листе и записываем его в результат декодирования, переходим снова в корень дерева.
Примечание: при передаче закодированных данных требуется также передавать дерево или таблицу частот, чтобы можно было восстановить дерево.
В данном примере, дуги помечались случайным образом, учитывалось только то, что на дугах, идущих к потомку узла должны быть разные значения.
Чтобы передавать таблицу частот нужно всегда помечать левую дугу 1, а правую 0 (или наоборот), чтобы можно было восстановить дерево по таблице.
Алгоритм Шеннона-Фано
Данный алгоритм получения префиксных кодов независимо друг от друга предложили Р. Фано и К. Шеннон, заключается он в следующем. На первом шаге все символы исходной информационной последовательности сортируются по убыванию или возрастанию вероятностей их появления (частоты их появления), после чего упорядоченный ряд символов в некотором месте делится на две части так, чтобы в каждой из них сумма частот символов была примерно одинакова. В качестве демонстрации рассмотрим слово «авиакатастрофа».
Если символы, составляющие данное слово, отсортировать по убыванию частоты их появления, то получим следующую последовательность: {а(5), т(2), в(1), и(1), к(1), с(1), р(1), о(1), ф(1)} (в скобках указывается частота повторяемости символа в слове). Далее, нам нужно разделить эту последовательность на две части так, чтобы в каждой из них сумма частот символов была примерно одинаковой (насколько это возможно). Понятно, что раздел пройдет между символами «т» и «в», в результате чего образуется две последовательности: {а(5), т(2)} и {в(1), и(1), к(1), с(1), р(1), о(1), ф(1)}. Причем суммы частот повторяемости символов в первой и второй последовательностях будут одинаковы и равны 7.
На первом шаге деления последовательности символов мы получаем первую цифру кода каждого символа. Правило здесь простое: для тех символов, которые оказались в последовательности слева, код будет начинаться с «0», а для тех, что справа — с «1».
Далее повторяем описанную процедуру для каждой из полученных таким делением последовательностей символов, поскольку каждая из них также упорядочена по частоте повторяемости символов.
В частности, последовательность {а(5), т(2)} разделится на два отдельных символа: a(5) и т(2) (других вариантов деления нет). Тогда вторая цифра кода для символа «a» — это «0», а для символа «т» — «1». Поскольку в результате деления последовательности мы получили отдельные элементы, то они более не делятся и для символа «a» получаем код 00, а для символа «т» — код 01.
Последовательность {в(1), и(1), к(1), с(1), р(1), о(1), ф(1)} можно разделить либо на последовательности {в(1), и(1), к(1)} и {с(1), р(1), о(1), ф(1)}, либо на {в(1), и(1), к(1)}, {с(1)} и {р(1), о(1), ф(1)}.
В первом случае суммы частот повторяемости символов в первой и второй последовательностях будут 3 и 4 соответственно, а во втором случае — 4 и 3 соответственно. Для определенности воспользуемся первым вариантом.
Для символов полученной новой последовательности {в(1), и(1), к(1)} (это левая последовательность) первые две цифры кода будут 10, а для последовательности {с(1), р(1), о(1), ф(1)} — 11.
Далее продолжаем описанную процедуру для каждой из полученных последовательностей до тех пор, пока в результате деления последовательностей в них будет оставаться не более одного символа.
В нашем примере получается следующая система префиксных кодов: «a» — 00, «т» — 01, «в» — 100, «и» — 1010, «к» — 1011, «с» — 1100, «р» — 1101, «о» — 1110, «ф» — 1111. Как нетрудно заметить, более короткие коды не являются началом более длинных кодов, то есть выполняется главное свойство префиксных кодов.
Схема алгоритма

Кодовое дерево:

Арифметическое сжатие
Согласно критерию Шеннона, оптимальным является такой код, в котором под каждый символ отводится код длиной –log2 p бит. И если, к примеру, вероятность какого-то символа составляет 0,2, то оптимальная длина его кода будет равна –log2 0,2 = 2,3 бит. Понятно, что префиксные коды не могут обеспечить такую длину кода, а потому не являются оптимальными. Вообще длина кода, определяемая критерием Шеннона, — это лишь теоретический предел. Вопрос лишь в том, какой способ кодирования позволяет максимально приблизиться к этому теоретическому пределу. Префиксные коды переменной длины эффективны и достаточно просты в реализации, однако существуют и более эффективные способы кодирования, в частности алгоритм арифметического кодирования.
Идея арифметического кодирования заключается в том, что вместо кодирования отдельных символов код присваивается одновременно всей информационной последовательности. При этом очевидно, что длина кода, приходящаяся на один отдельный символ, может быть и не целым числом. Именно поэтому такой способ кодирования гораздо эффективнее префиксного кодирования и более соответствует критерию Шеннона.
Идея алгоритма арифметического кодирования заключается в следующем. Как и во всех рассмотренных ранее способах кодирования, каждый символ исходной информационной последовательности характеризуется его вероятностью. Исходной незакодированной последовательности ставится в соответствие полуинтервал [0, 1). Далее, если информационное сообщение содержит N символов, то этот интервал делится на N отдельных полуинтервалов, каждый из которых соответствует какому-то символу. Причем длина полуинтервала, соответствующего какому-либо символу, равна вероятности этого символа. Поясним это на примере. Рассмотрим информационную последовательность слова «макака». Выпишем все символы, входящие в эту последовательность, с указанием их вероятности: {м(1/6), а(3/6), к(2/6)} (сортировка символов может быть произвольной). Далее, выделим на рабочем полуинтервале [0, 1) полуинтервал [0, 1/6), соответствующий символу «м» (длина полуинтервала равна вероятности символа). Затем сделаем то же самое для символа «а», которому будет соответствовать полуинтервал [1/6, 4/6) длиной 3/6. Символу «к» будет соответствовать полуинтервал [4/6, 1) длиной 2/6 (рис. 7).

В результате мы получим, что любое вещественное число из полуинтервала [0, 1) однозначно соответствует какому-то символу исходной информационной последовательности. К примеру, число 0,4 входит в полуинтервал [1/6, 4/6) и, следовательно, соответствует символу «а».
Представление символов информационного алфавита в соответствии с их вероятностями на рабочем полуинтервале [0, 1) — это подготовительный этап кодирования. Сам процесс кодирования заключается в следующем. Берется первый символ исходной информационной последовательности, и для него определяется соответствующий полуинтервал на рабочем отрезке. Далее этот полуинтервал становится новым рабочим отрезком, который также необходимо разбить на полуинтервалы в соответствии с вероятностями символов. Если бы мы захотели закодировать только один первый символ нашей последовательности, то на этом операция кодирования закончилась бы. Любое вещественное число из нового рабочего полуинтервала соответствовало бы нашему символу. Однако нам нужно закодировать не один символ, а их последовательность. Поэтому берем второй символ и определяем для него соответствующий полуинтервал уже на новом рабочем отрезке. Далее этот полуинтервал становится новым рабочим отрезком, который также необходимо разбить на полуинтервалы в соответствии с вероятностями символов. Причем этот рабочий полуинтервал уже соответствует двум символам информационной последовательности, то есть любое вещественное число из этого нового рабочего полуинтервала соответствует двум первым символам информационной последовательности. Продолжая такие итерации, мы, в конечном счете, получим некоторый полуинтервал, который соответствует всей исходной информационной последовательности.
На каждом шаге итерации необходимо пересчитывать границы всех полуинтервалов на новом рабочем полуинтервале. Пусть, к примеру, первому символу последовательности на рабочем полуинтервале [0, 1) соответствует полуинтервал [a, b), а второму символу — полуинтервал [c, d).
Поскольку на первом шаге кодирования новым рабочим полуинтервалом станет полуинтервал [a, b), то в этом рабочем полуинтервале второму символу будет соответствовать полуинтервал [a+(b–a)×c, a+(b–a)×d). То есть полуинтервал [c, d) сожмется в (b–a) раз. Любое число из полуинтервала [a+(b–a)×c, a+(b–a)×d) однозначно определяет последовательность двух первых символов.
Ну а теперь рассмотрим процесс кодирования на конкретном примере информационной последовательности слова «макака» (рис. 8).

Итак, первый символ — «м». На рабочем полуинтервале [0, 1) этому символу соответствует полуинтервал [0, 1/6), который становится новым рабочим полуинтервалом.
Далее, на новом рабочем полуинтервале [0, 1/6) откладываем полуинтервалы, соответствующие символам «м», «а» и «к». Символу «м» будет соответствовать уже полуинтервал [0, 1/36), символу «а» — полуинтервал [1/36, 4/36), а символу «к» — полуинтервал [4/36, 1/6). Отметим, что любое число из нового рабочего полуинтервала [0, 1/6) однозначно соответствует символу «м».
Следующий символ последовательности слова «макака» — это «а». На рабочем полуинтервале [0, 1/6) ему соответствует полуинтервал [1/36, 4/36), который и становится новым рабочим полуинтервалом. Далее, на новом рабочем полуинтервале [1/36, 4/36) откладываем полуинтервалы, соответствующие символам «м», «а» и «к». Символу «м» будет соответствовать уже полуинтервал [1/36, 3/72), символу «а» — полуинтервал [3/72, 3/36), а символу «к» — полуинтервал [3/36, 4/36). В данном случае важно, что уже любое вещественное число из рабочего полуинтервала [1/36, 4/36) представляет последовательность «ма».
Чтобы доказать это, рассмотрим число 1/36, входящее в этот полуинтервал. Поскольку это число входит в промежуток [0, 1/6), соответствующий символу «м» на исходном рабочем полуинтервале, то первый символ последовательности — это «м». Далее, необходимо отобразить (расширить) промежуток [0, 1/6) на исходный рабочий полуинтервал [0, 1). Для этого все точки полуинтервала [0, 1/6) делим на его длину (на 1/6). При этом число 1/36 перейдет в число 1/6. То есть мы как бы делаем обратное преобразование. Но число 1/6 на рабочем полуинтервале [0, 1) входит в промежуток [1/6, 4/6), соответствующий символу «а». Следовательно, второй символ последовательности — это «а».
Итак, мы выяснили, что число 1/36 из рабочего промежутка [1/36, 4/36) кодирует последовательность «ма». Пойдем дальше. Следующий символ последовательности «макака» — это «к». На рабочем полуинтервале [1/36, 4/36) ему соответствует промежуток [3/36, 4/36), который и становится новым рабочим полуинтервалом. Далее, на новом рабочем полуинтервале [3/36, 4/36) откладываем промежутки, соответствующие символам «м», «а» и «к». Символу «м» будет соответствовать уже полуинтервал [3/36, 19/216), символу «а» — полуинтервал [19/216, 22/216), а символу «к» — полуинтервал [22/216, 4/36). Любое вещественное число из рабочего полуинтервала [3/36, 4/36) представляет последовательность «мак». Теперь рассмотрим процесс раскодирования этой последовательности. Поскольку число 3/36 или 1/12 входит в полуинтервал [3/36, 4/36), покажем, что это число соответствует последовательности «мак».
Действительно, число 1/12 входит в промежуток [0, 1/6) на исходном рабочем полуинтервале, который соответствует символу «м». Следовательно первый символ — это «м». Далее, проецируем промежуток [0, 1/6) на промежуток [0, 1); при этом число 1/12 отобразится в число 1/2 на рабочем полуинтервале [0, 1). Поскольку число 1/2 входит в полуинтервал [1/6, 4/6), соответствующий символу «а», то второй символ последовательности — это «а». Затем необходимо спроецировать промежуток [1/6, 4/6) на рабочий полуинтервал [0, 1). При этом число 1/2 отобразится в число 2/3. Поскольку это число входит в промежуток [4/6, 1) на рабочем полуинтервале [0, 1), который соответствует символу «к», то третий символ последовательности — это «к».
Продолжая аналогичные действия по кодированию символов, мы придем к рабочему полуинтервалу [127/1296, 130/1296), который будет отвечать за все последовательности слова «макака» (рис. 8). Любое число из этого полуинтервала (например, 127/1296) однозначно определяет всю последовательность слова «макака» а обратное раскодирование осуществляется в шесть шагов.
Единственное, на чем имеет смысл остановиться при обратном раскодировании, это на процедуре проецирования полуинтервала [a, b) на полуинтервал [0, 1). При таком проецировании любая точка, принадлежащая промежутку [a, b), отобразится в точку x = (c – a)/(b – a), что легко доказать геометрически, используя обобщенную теорему Фалеса (рис. 9).

В качестве примера рассмотрим отображение промежутка [1/6, 2/3) на промежуток [0, 1). При таком проецировании число 1/2 из промежутка [1/6, 2/3) отобразится на число (1/2 – 1/6)/(2/3 – 1/6) = 2/3.
Итак, мы подробно рассмотрели процесс арифметического кодирования-декодирования. Отметим, что, в отличие от префиксного кодирования, в арифметическом кодировании символам не могут быть сопоставлены конкретные кодовые комбинации. Понятие «код» в данном случае несколько абстрактно и применимо только для информационной последовательности в целом. Здесь можно говорить только о вкладе, вносимом каждым символом, входящим в кодируемое информационное сообщение, в результирующую кодовую комбинацию. Этот вклад определяется длиной интервала, соответствующего символу, то есть вероятностью появления символа. Также отметим, что для возможности процесса декодирования декодер должен иметь информацию о том, какой именно промежуток соответствует каждому символу информационного алфавита на рабочем полуинтервале [0, 1). То есть данная информация является служебной и должна быть доступна декодеру.
До сих пор мы ничего не говорили о самом коде, который получится в результате арифметического кодирования. В рассмотренном нами примере со словом «макака» процесс арифметического кодирования завершился тем, что любое число из промежутка [127/1296, 130/1296) представляет последовательность «макака». Вопрос в том, какое именно число выбрать и как ему поставить в соответствие двоичный код. Можно использовать следующий способ: взять любое число из результирующего промежутка, перевести его в двоичную форму и отбросить целую часть двоичной дроби, равную нулю, — оставшаяся последовательность нулей и единиц и будет нашим кодом. Можно использовать и десятичное представление числа, но опять-таки использовать только дробную часть числа (отбросить ноль и десятичную запятую), представив ее в двоичном виде, который и задаст код последовательности.
Однако, не все так просто, как может показаться. Вообще, описанный нами алгоритм предполагает, что границы полуинтервалов представляются числами с неограниченной точностью. Кроме того, представляется проблемой выбор самого числа из конечного рабочего промежутка. Если, например, условиться использовать левую границу полуинтервала, то может оказаться, что она представляется в виде бесконечной десятичной дроби. Одним словом, при применении данного алгоритма возникает проблема манипуляций над числами, содержащими большое количество знаков после запятой.
Поэтому любая практическая реализация арифметического кодера должна основываться на операциях с целыми числами, которые не должны быть слишком длинными.
Идея заключается в том, чтобы числа, определяющие концы полуинтервалов, определялись бы целыми числами с разрядностью 16, 32 или 64 бита. Казалось бы, как это можно реализовать, если концы промежутков могут иметь неограниченное число знаков после запятой?
Прежде всего отметим, что все наши числа имеют вид 0,xxx… Поэтому 0 перед запятой можно отбросить и рассматривать лишь последовательности цифр после запятой. Далее, если концы всех промежутков выписать в десятичных дробях, можно заметить, что как только самые левые цифры чисел (рассматривается только дробная часть, то есть цифры после запятой), которые определяют концы рабочего полуинтервала на каждом шаге итерации, становятся одинаковыми, они уже не меняются в дальнейшем (на следующих итерациях). Отметим, что в нашем примере c последовательностью «макака» мало шагов итераций и даже на конечном шаге нет одинаковых левых цифр чисел, но при большем числе итераций они неизбежно появятся. Одинаковые цифры можно выдвинуть за скобки и работать с оставшейся дробной частью, которая ограничивается по длине. В ходе итераций уточняется последовательность цифр, выдвинутых за скобки, которая и представляет собой код.
Итак, метод арифметического кодирования — один из самых эффективных по степени сжатия алгоритмов, но скорость такого кодирования невысока.
Алгоритм LZW
Еще один распространенный алгоритм кодирования получил название LZW — по первым буквам фамилий его разработчиков: Lempel, Ziv и Welch (алгоритм Лемпеля—Зива—Велча).
Алгоритм был опубликован Велчем в 1984 году в качестве улучшенной реализации алгоритма LZ78, представленного Лемпелем и Зивом в 1978 году, и был запатентован фирмой Sperry.
Алгоритм LZW использует идею расширения информационного алфавита. Вместо традиционного 8-битного представления 256 символов ASCII-таблицы обычно используется 12-битное, что позволяет определить таблицу на 4096 записей.
Идея алгоритма LZW заключается в том, чтобы заменять строки символов некоторыми кодами, для чего и используется таблица на 4096 записей. Это делается без какого-либо анализа входной последовательности символов. При добавлении каждой новой строки символов просматривается таблица строк. Сжатие происходит, когда строка символов заменяется кодом. Первые 256 кодов (когда используются 8-битные символы) по умолчанию соответствуют стандартному набору символов, то есть значения кодов 0-255 соответствуют отдельным байтам. Остальные коды (256-4095) соответствуют строкам обрабатываемым алгоритмом.
По мере кодирования последовательно считываются символы входного потока и проверяется, есть ли в созданной таблице строк такая строка. Если она есть, то считывается следующий символ, а если нет, то в выходной поток заносится код для предыдущей найденной строки, в таблицу заносится новая строка и поиск начинается снова.
Рассмотрим в качестве примера входную последовательность ABCABCABCABCABCABC#. Маркер # будет символизировать конец исходного сообщения.
Для простоты будем считать, что используются только заглавные буквы английского алфавита (26 букв) и маркер # конца сообщения. Соответственно для перебора всех букв нашего алфавита достаточно 5 бит (25 = 32). Теперь предположим, что символы нашего алфавита кодируются по номеру буквы в алфавите от 1 до 26 следующим образом:
#=00000 (010)
A=00001 (110)
B=00010 (210)
C=00011 (310)
Последний символ Z будет иметь код 11010 (2610).
Отметим, что когда в нашей таблице кодов появится символ с кодом 32, то алгоритм должен перейти к 6-битным группам.
В нашем примере первый символ — это «A». Поскольку при инициализации в таблицу были занесены все односимвольные строки, то строка, соответствующая символу «A», в таблице есть (код символа 00001).
Далее считывается следующий символ «B» из входного потока и проверяется, есть ли строка «AB» в таблице. Такой строки в таблице пока нет. Поэтому данная строка заносится в таблицу с первым свободным кодом 100 000 (3210), а в выходной поток записывается код 00001, соответствующий предыдущему символу («A»).
Далее начинаем с символа, которым оканчивается последняя занесенная в таблицу строка, то есть с символа «B». Поскольку символ «B» есть в таблице, то считываем следующий символ «C». Строки «BC» в таблице нет, поэтому заносим эту строку в таблицу под кодом 100 001 (3310), а в выходной поток записывается код 00010, соответствующий предыдущему символу («В»).
Далее начинаем с символа, которым оканчивается последняя занесенная в таблицу строка, то есть с символа «С». Поскольку символ «С» есть в таблице, то считываем следующий символ «A». Строки «CA» нет в таблице, поэтому заносим эту строку в таблицу под кодом 100 010 (3410), а в выходной поток записывается код 00011, соответствующий предыдущему символу (символу «C»).
Затем начинаем с символа, которым оканчивается последняя занесенная в таблицу строка, то есть, с символа «A». Поскольку символ «A» есть в таблице, то считываем следующий символ «B». Строка «AB» уже есть в таблице, поэтому считываем следующий символ «C». Строки «ABC» нет в таблице, поэтому заносим эту строку в таблицу под кодом 100 011 (3510), а в выходной поток записывается код 100 000, соответствующий предыдущему символу в таблице (строке «AB»).
Далее начинаем с символа «C». Поскольку он уже есть в таблице, считываем следующий символ «A». Строка «CA» уже есть в таблице, поэтому считываем следующий символ «B». Строки «CAB» нет в таблице, поэтому заносим ее туда, а в выходной поток записываем код 100 010, соответствующий строке «CA».
Продолжая подобным образом, построим таблицу кодов для всего сообщения ABCABCABCABCABCABC# (табл. 1).
Особенность алгоритма LZW заключается в том, что для декодирования нет необходимости сохранять таблицу строк в файл для распаковки. Алгоритм построен таким образом, что можно восстановить таблицу строк, пользуясь только потоком кодов.
В заключение отметим, что алгоритм LZW находит применение в сжатии растровых изображений (форматы JPG, TIFF), а также в таком популярном формате, как PDF.
Задание:
Реализовать кодирование и декодирование информации заданным.
Вариант 1. Выполнить кодирование и декодирование русскоязычного текста методом Хаффмана.
Вариант 2. Выполнить кодирование и декодирование англоязычного текста методом Хаффмана.
Вариант 3. Выполнить кодирование и декодирование графического файла (BMP, GIF) методом Хаффмана.
Вариант 4. Выполнить кодирование и декодирование русскоязычного текста методом Шеннона-Фано.
Вариант 5. Выполнить кодирование и декодирование англоязычного текста методом Шеннона-Фано.
Вариант 6. Выполнить кодирование и декодирование графического файла (BMP, GIF) методом Шеннона-Фано.
Вариант 7. Выполнить кодирование и декодирование русскоязычного текста методом арифметического сжатия.
Вариант 8. Выполнить кодирование и декодирование англоязычного текста методом арифметического сжатия.
Вариант 9. Выполнить кодирование и декодирование русскоязычного текста используя алгоритм LZW.
Вариант 10. Выполнить кодирование и декодирование англоязычного текста используя алгоритм LZW.
Вариант 11 Выполнить кодирование и декодирование графического файла используя алгоритм LZW.
Отчет должен содержать описание алгоритма реализации, листинг кода с комментариями, исходные данные, результаты выполнения задания.