Понятие и представления комплексных чисел.
Определение 1.1. Комплексным числом z называется выражение вида z=x+iy, где x, y – действительные числа, а i – так называемая мнимая единица (i 2=-1). Число x называется действительной частью комплексного числа z и обозначается x =Re z, а y – мнимой частью z и обозначается y =Im z.
Множество комплексных чисел обозначают C. Множество действительных чисел R является подмножеством C (RÌC).
Определение 1.2. Два комплексных числа z 1= x 1+ iy 1 и z 2= x 2+ iy 2 называются равными (z 1= z 2) тогда и только тогда, когда равны их действительные части и равны их мнимые части: x 1= x 2, y 1= y 2.
Определение 1.3. Два комплексных числа z = x+iy и 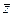 = x - iy называются сопряженными.
= x - iy называются сопряженными.
 Всякое комплексное число z=x+iy можно изобразить точкой M (x,y) плоскости О xy такой, что x =Re z, y =Im z.
Всякое комплексное число z=x+iy можно изобразить точкой M (x,y) плоскости О xy такой, что x =Re z, y =Im z.
Определение 1.4. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной осью, ось ординат называется мнимой осью.
Определение 1.5. Комплексное число z=x+iy можно изображать и с помощью радиус – вектора  . Длина вектора
. Длина вектора  , изображающего комплексное число z называется модулем этого числа и обозначается
, изображающего комплексное число z называется модулем этого числа и обозначается  или r. Модуль r =
или r. Модуль r =  однозначно определяется по формуле
однозначно определяется по формуле
 . (1.1)
. (1.1)
Величина угла между положительным направлением действительной оси и вектором  , изображающим комплексное число, называется аргументом этого числа, обозначается Arg z. Аргумент комплексного числа
, изображающим комплексное число, называется аргументом этого числа, обозначается Arg z. Аргумент комплексного числа 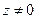 величина многозначная: Arg z =argz+2p k, k =0,±1,±2,…, где arg z = j - главное значение аргумента, заключенного в промежутке [0,2p).
величина многозначная: Arg z =argz+2p k, k =0,±1,±2,…, где arg z = j - главное значение аргумента, заключенного в промежутке [0,2p).
Определение 1.6. Запись числа z в виде z = x+iy называют алгебраической формой комплексного числа.
Определение 1.7. Запись числа z в виде
 (1.2)
(1.2)
называется тригонометрической формой комплексного числа. Аргумент j определяется из формул
 ,
,  ,
,  . (1.3)
. (1.3)
При переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить главное значение аргумента, которое находится по формуле
 (1.4)
(1.4)
Определение 1.8. Запись числа z в виде
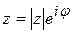 (1.5)
(1.5)
называется показательной формой комплексного числа.
Действия над комплексными числами
Основные действия над комплексными числами  и
и  , заданные в алгебраической форме, определяются следующими равенствами
, заданные в алгебраической форме, определяются следующими равенствами
 , (1.6)
, (1.6)
 , (1.7)
, (1.7)
 , (1.8)
, (1.8)
 , (
, (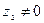 ) (1.9)
) (1.9)
При умножении комплексных чисел  и
и 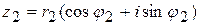 , заданных в тригонометрической форме их модули перемножаются, а аргументы складываются, т.е.
, заданных в тригонометрической форме их модули перемножаются, а аргументы складываются, т.е.
 . (1.10)
. (1.10)
Отсюда следует формула Муавра для возведения комплексных чисел в натуральную степень:
 . (1.11)
. (1.11)
Деление комплексных чисел, заданных в тригонометрической форме, осуществляется по формуле:
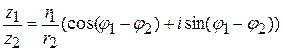 . (1.12)
. (1.12)
Корень n -й степени из комплексного числа имеет n различных значений, которые находятся по формуле
 , где k =0, 1, 2, …, n -1. (1.13)
, где k =0, 1, 2, …, n -1. (1.13)
Укажем основные свойства модуля и комплексного сопряжения
Свойства модуля:
1)  ,
, 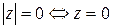 ; 2)
; 2)  ;
;
3) 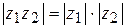 ; 4)
; 4)  . (1.14)
. (1.14)
Свойства комплексного сопряжения:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  .
.
(1.15)
Кривые и области в комплексной плоскости.
На комплексной плоскости могут располагаться различные кривые, уравнения которых необходимо уметь выражать в комплексной форме. Так, например, уравнение окружности радиуса R с центром в точке z 0 можно записать в виде  . Однако зачастую удобнее пользоваться параметрическим уравнением этой окружности в виде
. Однако зачастую удобнее пользоваться параметрическим уравнением этой окружности в виде  , где действительный параметр
, где действительный параметр  изменяется в пределах
изменяется в пределах  и представляет собой аргумент комплексного числа
и представляет собой аргумент комплексного числа  . Уравнение прямой, проходящей через точку
. Уравнение прямой, проходящей через точку  и наклоненной к действительной оси под углом
и наклоненной к действительной оси под углом  , можно записать в виде
, можно записать в виде  , где действительный параметр t изменяется в переделах
, где действительный параметр t изменяется в переделах  . Вообще, кривая на комплексной плоскости определяется заданием комплексной функции
. Вообще, кривая на комплексной плоскости определяется заданием комплексной функции  от некоторого действительного параметра t, изменяющегося на некотором интервале.
от некоторого действительного параметра t, изменяющегося на некотором интервале.
Весьма важно понятие области на комплексной плоскости. Под областью будем понимать часть комплексной плоскости, ограниченной одной или несколькими непрерывными кривыми. Строгое определение области дадим в следующей лекции. Приведем примеры некоторых областей в комплексной плоскости.
круг  ,
,  ;
;
кольцо 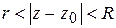 ,
,  ;
;
часть плоскости  ;
;
полуплоскость  или
или  , a, b – действительные числа;
, a, b – действительные числа;
полоса  или
или  , a, b – действительные числа;
, a, b – действительные числа;
 |

а) б)
 |

в) г)
в) г)
 | |||
 | |||
д) е)
Рис. 1.2.