Свойства и графики тригонометрических функций

Лекция 16

Тема «Тригонометрические функции»

Цель: закрепить знания о функциях, их свойствах и графиках.

План лекции:

1. Основные свойства функций.

2. Свойства и график у = sinx.

3. Свойства и график y = cosx.

4. Свойства и график y = tgx.

Функции и их графики

Определение. Числовой функцией с областью определения D называется соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу число у, зависящее от х.

При этом используют запись у = f(x).

Переменную х называют независимой переменной или аргументом, а переменную у – зависимой переменной или значением функции в точке х (говорят, что у является функцией от х).

Область определения функции f обозначают D(f). Множество, состоящее из всех чисел f(x), таких, что х принадлежит области определения функции f, называют областью значений функции f и обозначают E(f).

Чаще всего функцию обозначают какой – либо формулой.

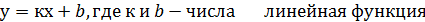
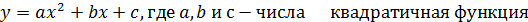
Определение. Графиком функции f называют множество всех точек (х;у) координатной плоскости, где у = f(х), а х «пробегает» всю область определения функции f.

Вы уже знакомы с графиками функций

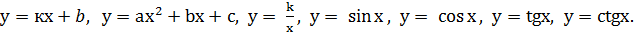
Определение. Функция f называется четной, если для любого х из ее области определения f(-x) = f(x).

Определение. Функция f называется нечетной, если для любого х из ее области определения f(-x) = - f(x).

График четной функции симметричен относительно оси ординат (ось Оу), а график нечетной функции симметричен относительно начала координат.

Очень многие процессы и явления, с которыми мы встречаемся на практике, имеют повторяющийся характер. Такого рода процессы называются периодическими, а функции, их описывающие, - периодическими функциями.

Определение. Функция f возрастает на множестве Р, если для любых х₁ и х₂ из множества Р, таких, что х₂ > х₁, выполнено неравенство f(х₂) > f(х₁).

Определение. Функция f убывает на множестве Р, если для любых х₁ и х₂ из множества Р, таких, что х₂ > х₁, выполнено неравенство f(х₂) < f(х₁).

Определение. Точка х₀ называется точкой минимума функции f, если для всех х некоторой окрестности х₀ выполнено неравенство f(х) 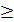f(х₀).

Определение. Точка х₀ называется точкой максимума функции f, если для всех х некоторой окрестности х₀ выполнено неравенство f(х) f(х₀).

 

Свойства и графики тригонометрических функций

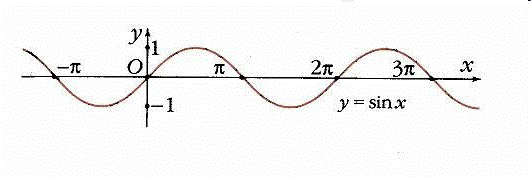
1. Область определения – множество всех действительных чисел.

2. Область значений E(f) – промежуток .

3. Функция нечетная: .

4. Функция периодическая. Наименьший положительный период равен 2p: .

5. Нули функции: при .

6. Промежутки знакопостоянства:

sin x > 0 при ,

sin x < 0 при .

7. Функция возрастает при и убывает при .

8. Функция принимает минимальные значения, равные -1, при и максимальные значения, равные 1, при .

График функции называют синусоидой.

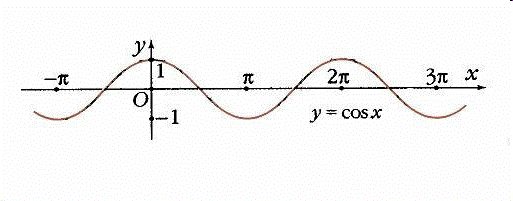
1. Область определения – множество всех действительных чисел.

2. Область значений E(f) – промежуток .

3. Функция четная: .

4. Функция периодическая. Наименьший положительный период равен 2p: .

5. Нули функции: при .

6. Промежутки знакопостоянства:

cos x > 0 при ,

cos x < 0 при .

7. Функция возрастает при и убывает при .

8. Функция принимает минимальные значения, равные -1, при и максимальные значения, равные 1, при .

График функции также называют синусоидой.

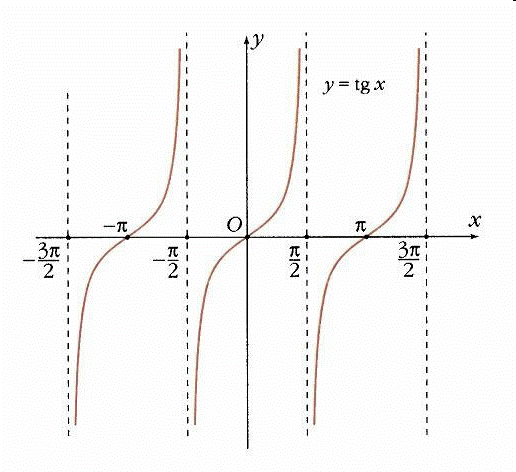
1. Область определения – множество всех действительных чисел, кроме чисел .

2. Область значений E(f) – множество всех действительных чисел.

3. Функция нечетная: .

4. Функция периодическая. Наименьший положительный период равен p: .

5. Нули функции: при .

6. Промежутки знакопостоянства:

tg x > 0 при ,

tg x < 0 при .

7. Функция возрастает в каждом из промежутков .

График функции называют тангенсоидой.

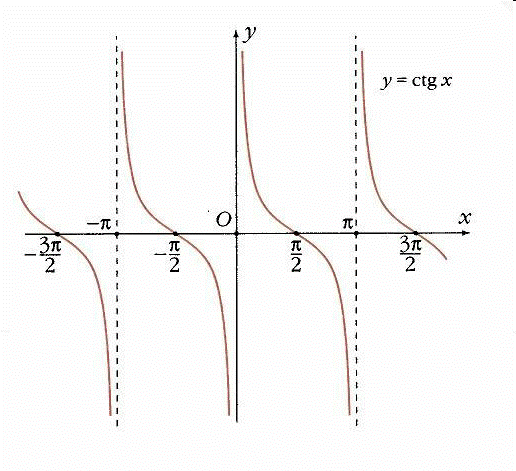
1. Область определения – множество всех действительных чисел, кроме чисел .

2. Область значений E(f) – множество всех действительных чисел.

3. Функция нечетная: .

4. Функция периодическая. Наименьший положительный период равен p: .

5. Нули функции: при .

6. Промежутки знакопостоянства:

ctg x > 0 при ,

ctg x < 0 при .

7. Функция убывает в каждом из промежутков .

 

Синус, косинус, тангенс и котангенс часто называют основными тригонометрическими функциями.

Пример 1. Пользуясь свойствами тригонометрических функций, замените выражение равным ему значением той же тригонометрической функции наименьшего положительного аргумента:

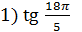Известно, что период функции тангенс равен 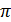. Получаем:

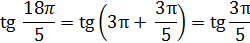
2) 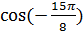Используем формулы приведения, четность и периодичность функции косинус , .

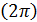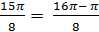Видеоматериал

https://yandex.ru/video/preview?filmId=3976625065512391987&parent-reqid=1607427441371408-499511705869061110500163-production-app-host-man-web-yp-181&path=wizard&text=тригонометрические+функции+их+свойства+и+графики&wiz_type=vital

Контрольные вопросы:

1. Что называется числовой функцией?

2. Что называется графиком функции?

3. Приведите пример четной функции и постройте ее график.

4. Приведите пример убывающей функции на всей области определения и постройте ее график.

5. Приведите пример функции, имеющей точку минимума и постройте ее график.

6. Какие существуют тригонометрические функции?

7. Перечислите свойства тригонометрических функций.

8. Пользуясь свойствами тригонометрических функций, замените выражение равным ему значением той же тригонометрической функции наименьшего положительного аргумента: 1) 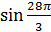; 2) .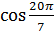

9. На графике функции y = cosx с областью определения 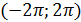отметьте период, нули функции, промежутки возрастания и убывания, точки минимума и максимума.