 . (26)
. (26)
 |
В этой формуле
 – плоская область, ограниченная конечным числом замкнутых, самонепересекающихся кусочно - гладких кривых,
– плоская область, ограниченная конечным числом замкнутых, самонепересекающихся кусочно - гладких кривых, 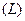 – граница области
– граница области  , проходимая в положительном направлении: так, чтобы область
, проходимая в положительном направлении: так, чтобы область  при движении вдоль кривой оставалась (для правой системы координат) слева (для левой системы координат, наоборот, оставалась справа);
при движении вдоль кривой оставалась (для правой системы координат) слева (для левой системы координат, наоборот, оставалась справа);  и их частные производные первого порядка непрерывны в замкнутой области
и их частные производные первого порядка непрерывны в замкнутой области 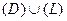 (рис. 15).
(рис. 15).
Рис. 15
 Докажем часть формулы (26):
Докажем часть формулы (26):
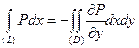 . (27)
. (27)
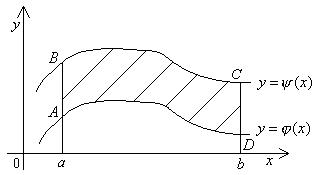
1. Пусть область 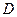 – криволинейная трапеция, ограниченная прямыми
– криволинейная трапеция, ограниченная прямыми 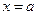 и
и 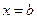 и непрерывными кривыми
и непрерывными кривыми  и
и 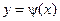 ,
, 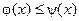 (рис. 16). Тогда
(рис. 16). Тогда
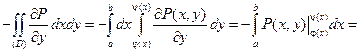
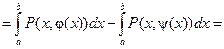
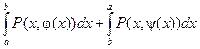 .
.
 |
Последнее выражение можно переписать в виде суммы двух криволинейных
Рис. 16
интегралов 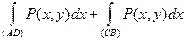 . Добавив сюда равные нулю
. Добавив сюда равные нулю 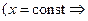
 интегралы
интегралы  и
и  , имеем:
, имеем: 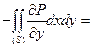
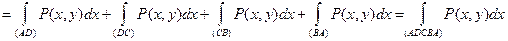 , т.е. получаем формулу (27).
, т.е. получаем формулу (27).
2. Чтобы получить формулу (27) для любой области, нужно разбить ее на криволинейные трапеции (мы будем рассматривать только области, для которых это возможно), к каждой из них применить (27) и сложить полученные равенства. В результате получим:
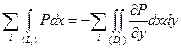 . (28)
. (28)
Правая часть этого равенства, очевидно, равна 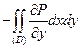 .
.
При сложении интегралов в левых частях интегралы по вертикальным перегородкам равны нулю, а интегралы по другим перегородкам взаимно уничтожаются, так как эти перегородки проходятся дважды, причем в противоположных направлениях (рис. 17). В результате
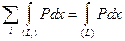 и
и 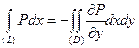 .
.
Рис. 17
 |
Аналогично, рассматривая криволинейные трапеции «вдоль» оси  получим,что
получим,что  . Следовательно,
. Следовательно, 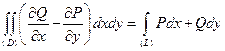 . ■
. ■
Пример. Вычислить 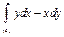 , где
, где 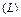 – замкнутый контур, изображенный на рис. 18.
– замкнутый контур, изображенный на рис. 18.
Рис. 18
Решение.
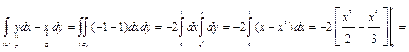
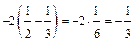 .
.
Обобщением формулы Грина на случай трех переменных является формула Стокса. Чтобы написать ее, дадим сначала следующее определение.
Определение 10. Ротором векторного поля  называется вектор
называется вектор

(естественно, вектор 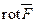 и его координаты зависят от точки М, т.е. от eе координат
и его координаты зависят от точки М, т.е. от eе координат  ).
).
Запомнить это определение можно при помощи следующей символической формулы:
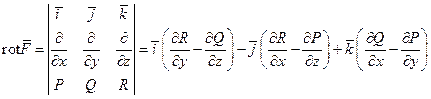
(раскладываем определитель по первой строке; получаемые при этом произведения рассматриваем как частные производные, например 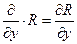 ).
).
Пример. Найти ротор того же поля, что выше: 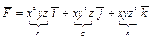
Решение.
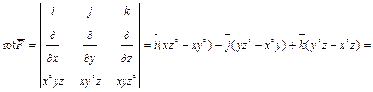
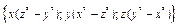 .
.
Теорема 9 (формула Стокса). Пусть в области  задано векторное поле
задано векторное поле  , где
, где 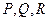 – непрерывны и имеют непрерывные частные производные. Пусть
– непрерывны и имеют непрерывные частные производные. Пусть 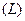 – замкнутый контур, ограничивающий двустороннюю поверхность
– замкнутый контур, ограничивающий двустороннюю поверхность 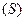 ,
, 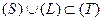 . Тогда
. Тогда
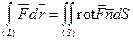 . (29)
. (29)
В этой формуле сторона поверхности 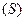 и направление обхода контура
и направление обхода контура 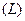 связаны следующим образом: если смотреть со стороны нормали к нашей стороне поверхности в точках, близких к
связаны следующим образом: если смотреть со стороны нормали к нашей стороне поверхности в точках, близких к 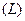 , то обход контура
, то обход контура 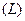 виден совершающимся против часовой стрелки (для правой системы координат, для левой системы координат – наоборот, по часовой стрелке). Или: наблюдатель, идущий по контуру так, что нормаль
виден совершающимся против часовой стрелки (для правой системы координат, для левой системы координат – наоборот, по часовой стрелке). Или: наблюдатель, идущий по контуру так, что нормаль 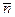 пронизывает его от ног до головы, должен видеть непосредственно прилегающую к нему часть поверхности слева от себя (для правой системы координат).
пронизывает его от ног до головы, должен видеть непосредственно прилегающую к нему часть поверхности слева от себя (для правой системы координат).
«Прочесть» формулу (29) можно следующим образом: циркуляция векторного поля 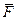 вдоль замкнутого контура
вдоль замкнутого контура 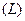 равна потоку ротора этого поля через поверхность, ограниченную данным контуром. При этом направление обхода
равна потоку ротора этого поля через поверхность, ограниченную данным контуром. При этом направление обхода 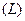 и сторона поверхности
и сторона поверхности 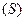 связаны по указанному выше правилу.
связаны по указанному выше правилу.
В соответствии с определениями циркуляции векторного поля, ротора этого поля и потока векторного поля через поверхность, формулу (29) можно переписать следующим образом:
 . (30)
. (30)
Для экономии места и времени доказательство этой формулы мы оставим за пределами данного текста.
Теперь мы можем провести доказательство достаточности условийтеоремы 5: если 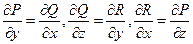 , то из формулы (30) следует, что для любого замкнутого контура
, то из формулы (30) следует, что для любого замкнутого контура  с натянутой на него поверхностью
с натянутой на него поверхностью 
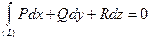 , а, в соответствии с теоремой 2, последнее равенство является необходимым и достаточным условием независимости интеграла от формы пути интегрирования.
, а, в соответствии с теоремой 2, последнее равенство является необходимым и достаточным условием независимости интеграла от формы пути интегрирования.
Инвариантное определение ротора векторного поля
Создается впечатление, что вектор 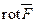 зависит от выбора системы координат. Покажем, что это не так. Возьмем точку
зависит от выбора системы координат. Покажем, что это не так. Возьмем точку 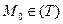 и любой единичный вектор
и любой единичный вектор 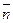 , исходящий из точки
, исходящий из точки  . «Окружим»
. «Окружим»  перпендикулярной к вектору
перпендикулярной к вектору 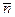 плоской площадкой
плоской площадкой 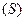 с границей
с границей 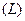 (рис. 19):
(рис. 19):
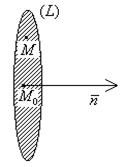 |
Рис. 19
Применим формулу Стокса: 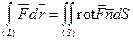 . Следующее равенство запишем на основании теоремы о среднем в поверхностном интеграле, которая аналогична теореме о среднем в двойном интеграле:
. Следующее равенство запишем на основании теоремы о среднем в поверхностном интеграле, которая аналогична теореме о среднем в двойном интеграле: 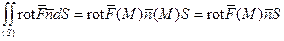 , где
, где 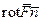 – скалярное произведение,
– скалярное произведение,  – площадь нашей площадки а
– площадь нашей площадки а 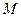 – некоторая ее точка. Отсюда
– некоторая ее точка. Отсюда 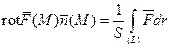 . Теперь будем стягивать площадку
. Теперь будем стягивать площадку 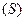 в точку
в точку  , тогда (частные производные функций
, тогда (частные производные функций 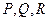 непрерывны) существует предел левой части последнего равенства:
непрерывны) существует предел левой части последнего равенства: 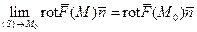 . Но тогда существует и предел правой части нашего равенства, и
. Но тогда существует и предел правой части нашего равенства, и
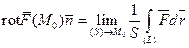 . (31)
. (31)
Но из определения циркуляции видно, что правая часть этой формулы не зависит от выбора системы координат, значит, и левая часть этой формулы тоже не зависит от выбора системы координат. Формула (31) задает 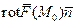 , т.е. (
, т.е. (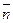 – единичный вектор) проекцию
– единичный вектор) проекцию  на любое направление. Формулу (31) можно взять за инвариантное определение
на любое направление. Формулу (31) можно взять за инвариантное определение 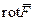 , т.е.
, т.е.  – это вектор, проекция которого на произвольное направление, определяемое вектором
– это вектор, проекция которого на произвольное направление, определяемое вектором 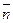 , задается этой формулой.
, задается этой формулой.
Оператор Гамильтона. Операции второго порядка
Введем символический вектор – оператор Гамильтона:  , где символ «
, где символ « » читается как «набла». Пользуясь этим символом, можно написать, что:
» читается как «набла». Пользуясь этим символом, можно написать, что:
1. Вектор 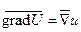 – это произведение вектора
– это произведение вектора  на число
на число 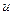 .
.
Действительно, при произведении вектора на число его координаты умножаются на это число: 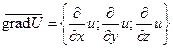 ; понимая эти произведения как частные
; понимая эти произведения как частные
производные, имеем:  .
.
2. Скаляр (число)  – это скалярное произведение векторов
– это скалярное произведение векторов  и
и 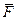 .
.
Действительно, считая скалярное произведение как сумму произведений координат векторов и понимая эти произведения как частные производные, имеем:  .
.
3. Вектор 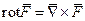 - это векторное произведение векторов
- это векторное произведение векторов  и
и 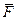 .
.
Действительно, находя векторное произведение и рассуждая, как выше, имеем: 
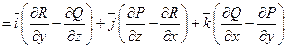 .
.
Операции второго порядка
Попробуем применить рассмотренные выше три операции первого порядка 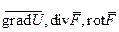 , переводящие, соответственно, скаляр в вектор, вектор в скаляр и вектор в вектор, друг к другу (там, где это возможно). Тогда мы получим пять операций второго порядка:
, переводящие, соответственно, скаляр в вектор, вектор в скаляр и вектор в вектор, друг к другу (там, где это возможно). Тогда мы получим пять операций второго порядка:  ,
,  .
.
Рассмотрим некоторые из этих операций:
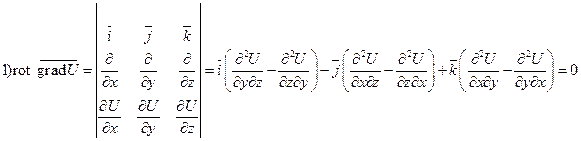 при выполнении условий теоремы о смешанных производных. Используя оператор Гамильтона, этот результат можно получить короче:
при выполнении условий теоремы о смешанных производных. Используя оператор Гамильтона, этот результат можно получить короче: 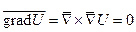 как векторное произведение коллинеарных векторов
как векторное произведение коллинеарных векторов  и
и 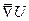 .
.
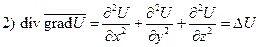 (
( – это так называемый оператор Лапласа).
– это так называемый оператор Лапласа).
3) 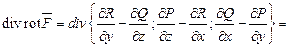
 при выполнении условий теоремы о смешанных производных. Или короче при помощи оператора Гамильтона:
при выполнении условий теоремы о смешанных производных. Или короче при помощи оператора Гамильтона:  как скалярное произведение ортогональных векторов
как скалярное произведение ортогональных векторов  и
и  .
.
Специальные векторные поля
Потенциальное поле
Определение 11. Векторное поле  называется потенциальным, если существует скалярное поле
называется потенциальным, если существует скалярное поле 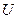 , называемое потенциалом, такое, что
, называемое потенциалом, такое, что  .
.
Теорема 10. Пусть в области (Т) функции 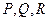 имеют непрерывные частные производные. Для того чтобы в этой области поле
имеют непрерывные частные производные. Для того чтобы в этой области поле 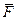 было потенциальным, необходимо и достаточно, чтобы
было потенциальным, необходимо и достаточно, чтобы  .
.
Необходимость этого условия уже доказана (см. выше).
 Достаточность. Пусть
Достаточность. Пусть  , т.е.
, т.е. 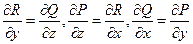 , тогда по теоремам 5 и 3 выражение
, тогда по теоремам 5 и 3 выражение 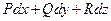 является дифференциалом некоторой функции
является дифференциалом некоторой функции  :
:  , откуда
, откуда 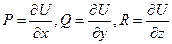 , т.е.
, т.е. 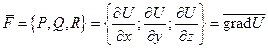 . ■
. ■
Замечание. При доказательстве теоремы 3 была получена и формула для нахождения потенциала U:
U(x,y,z)  . (32)
. (32)
В этой формуле векторное поле задано в области (Т), фиксированная точка 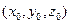 и точка
и точка  , в которой ищется потенциал, принадлежат этой области, а интеграл берется по любому пути, принадлежащему (Т) и соединяющему эти две точки. В частности, удобен путь по ломаной, звенья которой параллельны координатным осям. К правой части формулы (32), естественно, можно прибавить произвольную постоянную.
, в которой ищется потенциал, принадлежат этой области, а интеграл берется по любому пути, принадлежащему (Т) и соединяющему эти две точки. В частности, удобен путь по ломаной, звенья которой параллельны координатным осям. К правой части формулы (32), естественно, можно прибавить произвольную постоянную.
Пример. 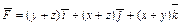 . Проверить, что это поле потенциально и найти его потенциал.
. Проверить, что это поле потенциально и найти его потенциал.
Решение. Найдем ротор этого поля:  поле потенциально и по формуле (32) его потенциал
поле потенциально и по формуле (32) его потенциал 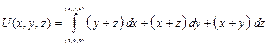 .
.
 |
Вычислим этот интеграл по изображенной на рис. 20, ломаной как сумму интегралов по ее звеньям:
Рис. 20
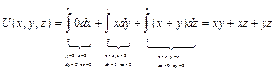 , что и заканчивает решение примера.
, что и заканчивает решение примера.
Отметим, что в потенциальном поле линейный интеграл 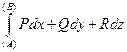 не зависит от формы пути интегрирования и, в силу формулы (6),
не зависит от формы пути интегрирования и, в силу формулы (6),
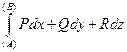 =
= 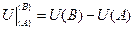 . (33)
. (33)
Соленоидальное поле
Определение 12. Векторное поле 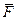 называется соленоидальным, если существует другое векторное поле
называется соленоидальным, если существует другое векторное поле  , называемое векторным потенциалом, такое, что
, называемое векторным потенциалом, такое, что 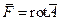 .
.
Теорема 11. Пусть в области (Т) функции  имеют непрерывные частные производные. Для того чтобы в этой области
имеют непрерывные частные производные. Для того чтобы в этой области 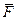 было соленоидальным, необходимо и достаточно, чтобы
было соленоидальным, необходимо и достаточно, чтобы  .
.
Необходимость этого условия была доказана ранее (см. выше).
 Достаточность. Пусть
Достаточность. Пусть  . Надо доказать, что существует
. Надо доказать, что существует  такое, что
такое, что
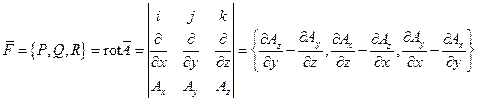 , т.е.
, т.е.
 . (34)
. (34)
Не пытаясь найти все решения этой системы, найдем одно частное ее решение. Положим  . Тогда
. Тогда 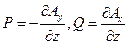 . Проверим, что уравнениям (34) удовлетворяют функции
. Проверим, что уравнениям (34) удовлетворяют функции
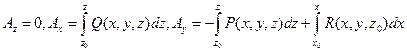 , (35)
, (35)
где 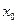 – фиксированная точка.
– фиксированная точка.
Действительно, дифференцируя интегралы по параметру и по верхнему пределу, имеем:
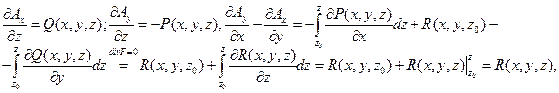
что и заканчивает доказательство теоремы. ■
Пример. Рассмотрим то же поле, что и выше: 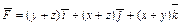 .
.
Решение.
Проверим, что оно не только потенциально, но и соленоидально и найдем его векторный потенциал.
Очевидно, что 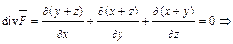 поле соленоидально. Найдем векторный потенциал по формулам (35), взяв в них
поле соленоидально. Найдем векторный потенциал по формулам (35), взяв в них  :
: 

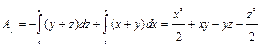 .
.
Т.е. 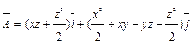 .
.